【提升版】浙教版数学九上4.1 比例线段同步练习

试卷更新日期：2024-09-27 类型：同步测试

进入出卷网下载

一、选择题

1. 若2x＝5y，则 $\frac{x}{y}$ 的值是（）

A、 $\frac{2}{5}$ B、 $\frac{5}{2}$ C、 $\frac{4}{5}$ D、 $\frac{5}{4}$

查看试题解析
2. 若四条线段a，b，c，d成比例，且a＝2cm，b $= \sqrt{2}$ cm，c $= \sqrt{6}$ cm，则线段d的长是（）

A、 $\sqrt{2}$ cm B、3 $\sqrt{2}$ cm C、 $\sqrt{3}$ cm D、2 $\sqrt{3}$ cm

查看试题解析
3. 若 $\frac{x}{y} = \frac{3}{4} (x y \neq 0)$ ，则下列等式成立的是（）

A、 $3 x = 4 y$ B、 $\frac{x + y}{y} = \frac{7}{4}$ C、 $\frac{x}{y + 1} = \frac{3}{5}$ D、 $\frac{x + 1}{y + 1} = \frac{3}{4}$

查看试题解析
4. 已知线段 $a = 4$ ， $b = 9$ ，线段 $x$ 是 $a$ ， $b$ 的比例中项，则 $x$ 等于（）

A、36 B、6 C、-6 D、6或-6

查看试题解析
5. 已知线段 $A B = 1$ ，点C是线段AB的黄金分割点，且 $A C > B C$ ，则线段AC的长是（）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{2 - \sqrt{5}}{2}$ C、 $\frac{3 - \sqrt{5}}{2}$ D、 $\frac{\sqrt{5} + 1}{2}$

查看试题解析
6. 黄金分割由于其美学性质，受到摄影爱好者和艺术家的喜爱，摄影中有一种拍摄手法叫黄金构图法．其原理是：如图，将正方形 $A B C D$ 的底边 $B C$ 取中点E ，以E为圆心，线段 $D E$ 为半径作圆，其与底边 $B C$ 的延长线交于点F ，这样就把正方形 $A B C D$ 延伸为矩形 $A B F G$ ，称其为黄金矩形．若 $C F = 4 a$ ，则 $A B =$ （）．

A、 $(\sqrt{5} - 1) a$ B、 $(2 \sqrt{5} - 2) a$ C、 $(\sqrt{5} + 1) a$ D、 $(2 \sqrt{5} + 2) a$

查看试题解析
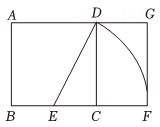7. “黔绣”的技师擅长在叶脉上飞针走绣，巧妙地将传统刺绣图案与树叶天然纹理完美结合，创作出神奇的“叶脉苗绣”作品．实际上，很多叶片本身都蕴含着黄金分割的比例，在大自然中呈现出优美的样子．如图，点P大致是 $A B$ 的黄金分割点 $(A P > P B)$ ，如果 $A P$ 的长为 $4 c m$ ，那么 $A B$ 的长约为（）

A、 $(2 \sqrt{5} + 2) c m$ B、 $(2 \sqrt{5} - 2) c m$ C、 $(2 \sqrt{5} + 1) c m$ D、 $(2 \sqrt{5} - 1) c m$

查看试题解析

二、填空题

8. 若 $\frac{a}{b} = \frac{5}{3}$ ，则 $\frac{a + b}{b}$ =.

查看试题解析
9. 大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”的美，如图，点P为 $A B$ 的黄金分割点 $(A P > P B)$ .如果 $B P$ 的长度为 $2 c m$ ，那么 $A P$ 的长度为 $c m$ .

查看试题解析
10. 已知线段 $b$ 是线段 $a$ 和线段 $c$ 的比例中项，若 $a = 2 cm$ ， $c = 8 cm$ ，则 $b =$ $cm$ ．

查看试题解析
11. 如图1，点 $C$ 把线段 $A B$ 分成两条线段 $A C$ 和 $B C$ ，如果 $\frac{A C}{A B} = \frac{B C}{A C}$ ，那么称线段 $A B$ 被点 $C$ 黄金分割，点 $C$ 叫做线段 $A B$ 的黄金分割点．设 $A B = a$ ， $A C = x$ ，则 $\frac{x}{a} = \frac{a - x}{x}$ ，所以 $\frac{x}{a} = \frac{\sqrt{5} - 1}{2}$ ，即 $\frac{A C}{A B} = \frac{\sqrt{5} - 1}{2}$ 叫做黄金比．一些美术家认为：人的上、下身长之比接近黄金比，可以增加美感．如图2的人体雕像高为 $m$ ，下身长为 $n$ ，为增加视觉美感，若图中 $m$ 为2米，则 $n$ 为米．

查看试题解析

三、解答题

12. 如图，我们知道，如果点 $P$ 是线段 $A B$ 上的一点，将线段分割成 $A P ， B P$ 两条线段 $(A P > B P)$ ，且满足 $B P ： A P = A P ： A B$ ，那么这种分割就叫做黄金分割．其中线段 $A P$ 与 $A B$ 的比值或线段 $B P$ 与 $A P$ 的比值叫做黄金分割数．已知比例的基本性质：对于长度为 $a ， b ， c ， d$ 的四条线段，如果 $a ： b = c ： d$ ，则 $a d = b c$ ．求黄金分割数（结果保留根号）．

查看试题解析
13.

(1)、解方程： $x^{2} - 4 x + 3 = 0$ ；

(2)、如果四条成比例线段线段的长分别为2，3，6， $a$ ，求 $a$ 的值．

查看试题解析
14. 已知：线段a，b，c，且 $\frac{a}{3} = \frac{b}{4} = \frac{c}{5}$ .

(1)、求 $\frac{a + b}{b}$ 的值；

(2)、如果对于线段a，b，c，满足a+b+c=36，求a，b，c的值.

查看试题解析
15. 如图，在平面直角坐标系中，已知四边形 $O A B C$ 是矩形，且 $O A = 8$ ， $O C = 6$ ， $C E ： B E = 1 ： 3$ ．反比例函数 $y = \frac{k_{1}}{x} (x > 0)$ 的图象分别交 $B C$ 、 $A B$ 于点E、点F．

(1)、求反比例函数的解析式；

(2)、连接 $E F$ 、 $O E$ 、 $O F$ ，求 $△ O E F$ 的面积；

(3)、是否存在x轴上的一点P，使得 $△ E F P$ 是不以点P为直角顶点的直角三角形？若存在，请直接写出符合题意的点P的坐标；若不存在，请说明理由．

查看试题解析

【提升版】浙教版数学九上4.1 比例线段 同步练习

一、选择题

二、填空题

三、解答题

【提升版】浙教版数学九上4.1 比例线段同步练习