【培优版】浙教版数学九上3.8 弧长及扇形面积 同步练习
试卷更新日期:2024-09-27 类型:同步测试
一、选择题
-
1. 如图,▱中, , , 以为直径的交于点 , 则的长为( )
 A、 B、 C、 D、2. 如图,在等腰三角形ABC中, , 以AB为直径作半圆,与AC,BC分别相交于点D,E,则的长度为( )
A、 B、 C、 D、2. 如图,在等腰三角形ABC中, , 以AB为直径作半圆,与AC,BC分别相交于点D,E,则的长度为( ) A、 B、 C、 D、3. 如图,在中,直径 , 点D为AB上方圆上的一点, , 于点E , 点P是OE上一点,连接DP , AP , 得出下列结论:
A、 B、 C、 D、3. 如图,在中,直径 , 点D为AB上方圆上的一点, , 于点E , 点P是OE上一点,连接DP , AP , 得出下列结论:Ⅰ:阴影部分的面积随着点P的位置的改变而改变,其最小值为 .
Ⅱ:阴影部分的周长随着点P的位置的改变而改变,其最小值为 .

下列判断正确的是( ).
A、只有Ⅰ正确 B、只有Ⅱ正确 C、Ⅰ、Ⅱ都正确 D、Ⅰ、Ⅱ都不正确4. 如图,折扇的骨柄长为7,折扇扇面宽度是折扇骨柄长的 , 折扇张开的角度为 , 则这把折扇扇面面积为( ) A、 B、 C、 D、5. 如图,Rt△ABC中, , 是△ABC的内切圆,切点分别为点D、E、F , , 则劣弧EF的长是( )
A、 B、 C、 D、5. 如图,Rt△ABC中, , 是△ABC的内切圆,切点分别为点D、E、F , , 则劣弧EF的长是( ) A、 B、 C、 D、6. 两个半径相等的半圆按如图方式放置,半圆的一个直径端点与半圆的圆心重合.若半圆的半径为2,则阴影部分的面积是( )
A、 B、 C、 D、6. 两个半径相等的半圆按如图方式放置,半圆的一个直径端点与半圆的圆心重合.若半圆的半径为2,则阴影部分的面积是( ) A、 B、 C、 D、7. 如图,正方形的边长为6,将长为的线段的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在上滑动,同时点F在上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段的中点M所经过的路线长为( )
A、 B、 C、 D、7. 如图,正方形的边长为6,将长为的线段的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在上滑动,同时点F在上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段的中点M所经过的路线长为( ) A、 B、 C、 D、8. 如图,中, , , BO=2cm,将绕点O逆时针旋转至 , 点在BO的延长线上,则边BC扫过区域(图中阴影部分)的面积为( )
A、 B、 C、 D、8. 如图,中, , , BO=2cm,将绕点O逆时针旋转至 , 点在BO的延长线上,则边BC扫过区域(图中阴影部分)的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,中, , , , 以为圆心,为半径的圆弧分别交、于点、 , 则图中阴影部分面积之和为 .
 10. 如图,是某十字路口机动车转弯时的示意图,设计转弯半径 , 转弯角度 , 大型机动车实际转弯时,转弯半径 , 转弯角度 , 则大型机动车转弯实际行驶路程(的长)与设计转弯行驶路程(AB的长)的差为(结果保留).
10. 如图,是某十字路口机动车转弯时的示意图,设计转弯半径 , 转弯角度 , 大型机动车实际转弯时,转弯半径 , 转弯角度 , 则大型机动车转弯实际行驶路程(的长)与设计转弯行驶路程(AB的长)的差为(结果保留). 11. 如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,弧BE的长为 ,则图中阴影部分的面积为 .
11. 如图,以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,弧BE的长为 ,则图中阴影部分的面积为 . 12. 如图,正六边形的边长为2,以为圆心,的长为半径画弧,得 , 连接 , , 则图中阴影部分的面积为 .
12. 如图,正六边形的边长为2,以为圆心,的长为半径画弧,得 , 连接 , , 则图中阴影部分的面积为 .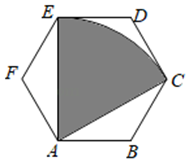 13. 如图,正方形的边长为2,以A为圆心,长为半径画.以D为圆心,长为半径画 , 形成如图“杯子”样的阴影部分,则阴影部分的面积为.
13. 如图,正方形的边长为2,以A为圆心,长为半径画.以D为圆心,长为半径画 , 形成如图“杯子”样的阴影部分,则阴影部分的面积为.
三、解答题
-
14. 如图, 内接于 交 于点 交 于点 , 交 于点 , 连结 .
 (1)、求证: .(2)、 若 的半径为 , 求 的长 (结果保留 ).15. 如图,以等腰AABC的底边BC为直径作半圆,交AB,AC于点D,E.
(1)、求证: .(2)、 若 的半径为 , 求 的长 (结果保留 ).15. 如图,以等腰AABC的底边BC为直径作半圆,交AB,AC于点D,E. (1)、证明:(2)、若∠A=60°,BC=2,求阴影部分面积.16. 如图1所示,草坪上的喷水装置高 , 喷头一瞬间喷出的水流呈抛物线状,喷出的抛物线水流在与喷水装置的水平距离为处,达到最高点 , 点距离地面 .
(1)、证明:(2)、若∠A=60°,BC=2,求阴影部分面积.16. 如图1所示,草坪上的喷水装置高 , 喷头一瞬间喷出的水流呈抛物线状,喷出的抛物线水流在与喷水装置的水平距离为处,达到最高点 , 点距离地面 . (1)、请建立适当的平面直角坐标系 , 求出该坐标系中水流所呈现的抛物线的解析式;(2)、这个喷水装置的喷头能旋转 , 它的喷灌区域是一个扇形,如图2所示,求出它能喷灌的草坪的面积(取3,结果保留整数).
(1)、请建立适当的平面直角坐标系 , 求出该坐标系中水流所呈现的抛物线的解析式;(2)、这个喷水装置的喷头能旋转 , 它的喷灌区域是一个扇形,如图2所示,求出它能喷灌的草坪的面积(取3,结果保留整数).四、实践探究题
-
17. 综合探究
将两块三角板如图1所示放置,∠ACB=90°,∠BAC=45°,∠CDE=90°,∠DCE=30°,AC=CD=6.将△DCE 绕着点C顺时针旋转时CF平分∠BCD.
 (1)、如图1,当CD边与CA边重合时,求∠ECF的度数;(2)、如图2,在旋转过程中,当∠ACD=2∠ECF时,求线段CD扫过的面积(结果保留π);(3)、当边CD与CB重合时停止旋转,探究∠ACD与∠ECF满足的数量关系,并说明理由.18.根据背景素材,探索解决问题.
(1)、如图1,当CD边与CA边重合时,求∠ECF的度数;(2)、如图2,在旋转过程中,当∠ACD=2∠ECF时,求线段CD扫过的面积(结果保留π);(3)、当边CD与CB重合时停止旋转,探究∠ACD与∠ECF满足的数量关系,并说明理由.18.根据背景素材,探索解决问题.生活中的数学——自动旋转式洒水喷头如何灌溉草坪
背景素材
数学来源于生活,九4班分四个小组,开展数学项目式实践活动,获取所有数据共享,对草坪喷水管建立数学模型.草坪装有1个自动旋转式洒水喷头,灌溉园林草坪.如图1所示,观察喷头可顺、逆时针往返喷洒.

甲小组在图2中建立合适的直角坐标系,喷水口中心O有一喷水管OA , 从A点向外喷水,喷出的水柱最外层的形状为抛物线.以水平方向为x轴,点O为原点建立平面直角坐标系,点A(喷水口)在y轴上,x轴上的点D为水柱的最外落水点.
乙小组在甲小组基础上,测量得距洒水喷头水平距离较远若干米的E处,正上方有一树枝叶F , 旋转式喷洒水柱外端刚好碰到树叶F的最低处.
丙小组在甲小组基础上,测量得喷水口中心O到水柱的最外落水点D距离为半径,建立⊙O半径为OD的扇形平面图(图3).
问题解决
任务1
获取数据
丁小组测量得喷头的高米,喷水口中心点O到水柱的最外落水点D水平距离为8米,经过点 .
解决问题
求出水柱所在抛物线的函数解析式.
任务2
获取数据
丁小组测树叶F距水平地面最低高度米,点F在抛物线上且离水喷头水平距离较远,E在OD上,OD⊥EF .
解决问题
求OE的长.
任务3
推理计算
丁小组观察自动旋转式洒水喷头可顺、逆时针往返喷洒,可平面旋转角度不超过240°,求:
①这个喷头最多可洒水多少平方米?
②在①条件下,此时DD'的长.
19. 数学活动课上,某小组将一个含45°的三角尺AEF和一个正方形纸板ABCD如图1摆放,若AE=1,AB=2.将三角尺AEF绕点A逆时针方向旋转α(0°≤α≤90°)角,观察图形的变化,完成探究活动.
(1)、【初步探究】
如图2,连接BE,DF并延长,延长线相交于点G,BG交AD于点M.
问题1 BE和DF的数量关系是 , 位置关系是 .(2)、【深入探究】
应用问题1的结论解决下面的问题.
问题2 如图3,连接BD,点O是BD的中点,连接OA,OG.求证OA=OD=OG.(3)、【尝试应用】
问题3 如图4,请直接写出当旋转角α从0°变化到60°时,点G经过路线的长度.五、综合题

