【培优版】浙教版数学九上3.7 正多边形 同步练习
试卷更新日期：2024-09-27 类型：同步测试
一、选择题
-
1. 刘徽在《九章算术注》中首创“割圆术”，利用圆的内接正多边形来确定圆周率，开创了中国数学发展史上圆周率研究的新纪元．某同学在学习“割圆术”的过程中，作了一个如图所示的圆内接正十二边形．若的半径为1，则这个圆内接正十二边形的面积为（ ）
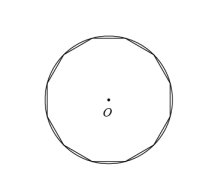A、1 B、3 C、 D、2. 如图，正五边形内接于 ， 点F为劣弧上的一点，则的度数为（ ）
A、36° B、45° C、60° D、72°3. 如图，用一些全等的正五边形按如图方式可以拼成一个环状，使相邻的两个正五边形有公共顶点，所夹的锐角为24°，图中所示的是前3个正五边形拼接的情况，拼接一圈后，中间会形成一个正多边形，则该正多边形的边数是（ ）
A、4 B、5 C、6 D、74. 将正六边形与正五边形按如图所示方式摆放，公共顶点为O，且正六边形的边AB与正五边形的边DE在同一条直线上，则∠COF的度数是（ ）
A、74° B、76° C、84° D、86°5. 如图，正五边形的外接圆为为劣弧上一点，则（ ）
A、 B、 C、 D、6. 一个适当大的正六边形，它的一个顶点与一个边长为定值的小正六边形 的中心 重合，且与边 、 相交于 、 （如图）.图中阴影部分的面积记为 ，三条线段 、 、 的长度之和记为 ，在大正六边形绕点 旋转过程中，下列说法正确的是（ ）
A、 变化， 不变 B、 不变， 变化 C、 变化， 变化 D、 与 均不变7. 如图，在正五边形中，作于 ， 连接与交于下列结论，错误的是( )
A、 B、 C、 D、8. 如图1，在边长为2的正六边形ABCDEF中，M是BC的中点，连接EM交AD于N点，若 ， 则表示实数a的点落在数轴上（如图2）标有四段中的（ ）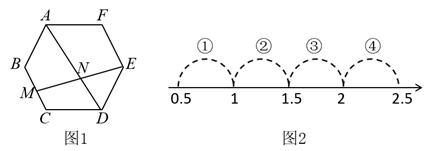
A、段① B、段② C、段③ D、段④9. 如图，点是的八等分点．若 ， 四边形的周长分别为a，b，则下列说法正确的是（ ）
A、 B、 C、 D、a，b大小无法比较二、填空题
-
10. 足球表面为什么用正六边形和正五边形构成？因为正六边形的两个内角和正五边形的一个内角加起来接近一个周角，而又不足一个周角．这样，由平面折叠而成的多面体充气后最终就呈现为球形．如图，在折叠前的平面上，拼接点处的缝隙∠AOB的大小为°．
11. 三个能够重合的正六边形的位置如图．已知B点的坐标是 ， 则A点的坐标是 ．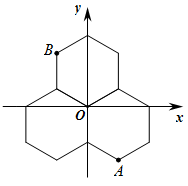
12. 如图，正六边形的中心为原点 ， 顶点 ， 在轴上，且半径为 ， 则点和点的坐标分别为 ．
13. 如图摆放的两个正六边形的顶点A，B，C，D在圆上．若 ， 则该圆的半径为 ．
三、解答题
-
14. 已知一个正多边形的内角和比外角和的3倍多 ， 求这个正多边形的边数和每个内角的度数.15. 如图，ABCDE为正五边形．
(1)、求∠A的度数；(2)、连接BD，CE，求证：BD＝CE．四、实践探究题
-
16. 这些图形中的边与角有什么共同特征？
一般地，我们把各边相等、各内角也相等的多边形叫做正多边形（regular polygon）．边数为五的正多边形叫做正五边形（如图2），边数为六的正多边形叫做正六边形，如图3的两个正多边形分别是正七边形和正八边形．
正多边形有许多优良的性质，匀称美观，常被人们用于图案设计和镶嵌平面（既不留空隙，又不相重叠地拼接）（图4）．
五、综合题
-
17. 问题背景：某课外学习小组在一次学习研讨中，得到如下命题题设，请分别补充结论，不用证明．
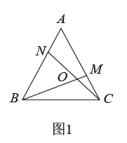
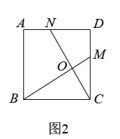
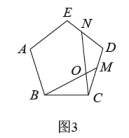
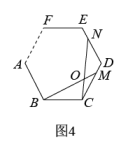(1)、如图1，在正三角形ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON＝60°，则BM与CN有何大小关系？(2)、如图2，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON＝90°，则BM与CN有何大小关系？(3)、学习小组成员根据上述两个命题运用类比的思想又提出了如下的问题：如图3，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON＝108°，则BM与CN的大小关系是怎样的？请说明理由．(4)、请你继续完成下面的探索：如图4，在正n边形（n≥3）中，M、N分别是CD、DE上的点，BM与CN相交于点O，问当∠BON等于多少度时，结论BM＝CN成立？（不要求证明）
-