【基础版】浙教版数学九上3.7 正多边形 同步练习

试卷更新日期：2024-09-27 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 正n边形的中心角是30°，n=（ ）
    A、6 B、8 C、10 D、12

    查看试题解析

  • 2. 正十二边形的一个外角的度数为（   ）
    A、30° B、36° C、144° D、150°

    查看试题解析

  • 3. 如图，在正六边形ABCDEF中，以AB为边作正五边形ABGHI，则∠FAI的度数为（    ）

    A、10° B、12° C、14° D、15°

    查看试题解析

  • 4. 如图， 在正五边形中， BE是对角线， AF⊥BE交CD于点F ，  则∠BAF的度数为（　　）

    A、30∘ B、36∘ C、40∘ D、54∘

    查看试题解析

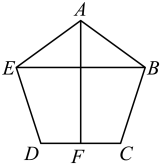  • 5. 如图，正六边形ABCDEF内接于⊙O ， OA＝1，则AB的长为（      ）

    A、2 B、3 C、1 D、12

    查看试题解析

  • 6. 如图，平面直角坐标系中，原点O为正六边形ABCDEF的中心，EF//x轴，点E在双曲线y=kx（k为常数，k>0）上，将正六边形ABCDEF向上平移3个单位长度，点D恰好落在双曲线上，则k的值为（      ）

    A、43 B、33 C、23 D、3

    查看试题解析

  • 7. 如图，是正n边形纸片的一部分，其中l ， m是正n边形两条边的一部分，若l ， m所在的直线相交形成的锐角为60° ， 则n的值是( )

    A、5 B、6 C、8 D、10

    查看试题解析

  • 8. 如图，已知AB ， BC ， CD是正n边形的三条边，在同一平面内，以BC为边在该正n边形的外部作正方形BCMN ． 若∠ABN＝120°，则n的值为（　　）

    A、12 B、10 C、8 D、6

    查看试题解析

二、填空题

  • 9. 一个正多边形它的一个内角恰好是一个外角的4倍，则这个正多边形是边形．

    查看试题解析

  • 10. 如图，在正五边形ABCDE内，以CD为边作等边△CDF ， 则∠BFC的数为 ．

    查看试题解析

  • 11. 如图是我国清代康熙年间的八角青花碗，其轮廓是一个正八边形，正八边形的每一个内角是 ．

    查看试题解析

  • 12. 如图，AB是⊙O的内接正n边形的一边，点C在⊙O上，∠ACB＝18°，则n＝ ．

    查看试题解析

三、解答题

  • 13. 用一条宽相等的足够长的纸条打一个结，如图①所示，然后轻轻拉紧、压平，就可以得到如图②所示的正五边形ABCDE．求∠BAC的度数．

    查看试题解析

  • 14. 将一个正六边形的纸片对折，并完全重合．那么得到的图形是几边形？它的内角和（按一层计算）是多少度？

    查看试题解析

  • 15. 如图1，正五边形ABCDE内接于⊙O，阅读以下作图过程，并回答下列问题：

    作法如图⒉

    1.作直径AF.

    2.以F为圆心，FO为半径作圆弧，与⊙O交于点M，N.

    3.连结AM，MN，NA.

    (1)、求∠ABC的度数.
    (2)、△AMN是正三角形吗？请说明理由.
    (3)、从点A开始，以DN长为半径，在⊙O上依次截取点，再依次连结这些等分点，得到正n边形，求n的值.

    查看试题解析