人教版八年级上学期数学第十二章质量检测(进阶)
试卷更新日期:2024-09-27 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,在△ABC和△DCE中,点B、D、C在同一直线上,已知∠ACB=∠E,BC=CE,添加以下条件后,仍不能判定△ABC≌△DCE的是( )
 A、AB=CD B、 C、AC=DE D、∠B=∠DCE2. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,AB=10,∠CAB和∠ABC的平分线交于点O,OM⊥BC于点M,则OM的长为( )
A、AB=CD B、 C、AC=DE D、∠B=∠DCE2. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,AB=10,∠CAB和∠ABC的平分线交于点O,OM⊥BC于点M,则OM的长为( ) A、1 B、2 C、3 D、43. 在如图所示的5×5方格中,每个小方格都是边长为1的正方形,是格点三角形(即顶点恰好是正方形的顶点),则与有一条公共边且全等的所有格点三角形的个数是( )
A、1 B、2 C、3 D、43. 在如图所示的5×5方格中,每个小方格都是边长为1的正方形,是格点三角形(即顶点恰好是正方形的顶点),则与有一条公共边且全等的所有格点三角形的个数是( ) A、1 B、2 C、3 D、44. 如图,在 ABC和 BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于( )
A、1 B、2 C、3 D、44. 如图,在 ABC和 BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于( ) A、∠EDB B、∠BED C、 ∠AFB D、2∠ABF5. 如图,在四边形中, , 连接 , 取 , 连接 , 下列条件中不一定能判定的是
A、∠EDB B、∠BED C、 ∠AFB D、2∠ABF5. 如图,在四边形中, , 连接 , 取 , 连接 , 下列条件中不一定能判定的是 A、 B、 C、 D、6. 如图,△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=8,DE=3,则△BCE的面积等于( )
A、 B、 C、 D、6. 如图,△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=8,DE=3,则△BCE的面积等于( ) A、11 B、8 C、12 D、37. 如图,小虎用10块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板 , 点C在上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离的长度为( )
A、11 B、8 C、12 D、37. 如图,小虎用10块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板 , 点C在上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离的长度为( )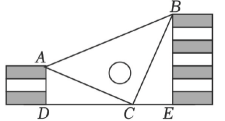 A、 B、 C、 D、8. 如图, , , , 点在线段上以的速度由点向点运动,同时,点在线段上以的速度由点向点运动,它们运动的时间为 . 当与全等时,的值是( )
A、 B、 C、 D、8. 如图, , , , 点在线段上以的速度由点向点运动,同时,点在线段上以的速度由点向点运动,它们运动的时间为 . 当与全等时,的值是( ) A、2 B、3或1.5 C、2或1.5 D、2或39. 如图,中, , 的角平分线、相交于点 , 过作交的延长线于点 , 交于点 , 则下列结论:①;②;③;④ , 其中正确的有( )
A、2 B、3或1.5 C、2或1.5 D、2或39. 如图,中, , 的角平分线、相交于点 , 过作交的延长线于点 , 交于点 , 则下列结论:①;②;③;④ , 其中正确的有( ) A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题(每题3分,共15分)
-
10. 如图, , 点A,D,B,C分别在直线MN与PQ上,点在AB上, , , 则.
 11. 如图所示,和的角平分线相交于点P, , 则的度数为 .
11. 如图所示,和的角平分线相交于点P, , 则的度数为 . 12. 如图,是的角平分线,于点 , , 和的面积分别为26和16,则的面积为 .
12. 如图,是的角平分线,于点 , , 和的面积分别为26和16,则的面积为 . 13. 如图,已知和交于点 , 若点、共线,时,则 .
13. 如图,已知和交于点 , 若点、共线,时,则 .
三、解答题(共7题,共62分)
-
14.
 (1)、模型的发现:
(1)、模型的发现:如图 , 在中, , , 直线经过点 , 且 , 两点在直线的同侧,直线 , 直线 , 垂足分别为点、问:、和的数量关系.
(2)、模型的迁移:位置的改变如图 , 在的条件下,若、两点在直线的异侧,请说明、和的数量关系,并证明.
15. 如图,中,点D在边上, , 的平分线交于点E , 过点E作 , 垂足为 , 且 , 连接 . (1)、求证:平分;(2)、若 , 求的面积.16. 小明和爸爸妈妈在公园里荡秋千如图,小明坐在秋千上的起始位置处,起始位置与地面垂直,两脚在地面上用力一蹬,妈妈在距地面米高的处接住他,然后用力一推,爸爸在处接住他若妈妈与爸爸到秋千起始位置的水平距离米,米,且 , 求爸爸接住小明的位置距地面的高度.
(1)、求证:平分;(2)、若 , 求的面积.16. 小明和爸爸妈妈在公园里荡秋千如图,小明坐在秋千上的起始位置处,起始位置与地面垂直,两脚在地面上用力一蹬,妈妈在距地面米高的处接住他,然后用力一推,爸爸在处接住他若妈妈与爸爸到秋千起始位置的水平距离米,米,且 , 求爸爸接住小明的位置距地面的高度. 17. 如图,点 , , , 在同一条直线上,点 , 分别在直线的两侧,且 , , .
17. 如图,点 , , , 在同一条直线上,点 , 分别在直线的两侧,且 , , . (1)、求证:;(2)、若 , , 求的长.18. 如图,中, , 点分别在边上, , .
(1)、求证:;(2)、若 , , 求的长.18. 如图,中, , 点分别在边上, , .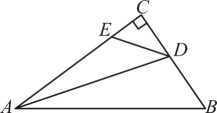 (1)、求证:平分;(2)、写出与的数量关系,并说明理由.19. 如图,已知 , , , , 与相交于点 .
(1)、求证:平分;(2)、写出与的数量关系,并说明理由.19. 如图,已知 , , , , 与相交于点 . (1)、求证:;(2)、求证: .20. 小红在数学课上学习了角的相关知识后,立即对角产生了浓厚的兴趣.她查阅书籍发现两个有趣的概念,三角形中相邻两条边的夹角叫做三角形的内角;三角形一条边的延长线与其邻边的夹角,叫做三角形的外角.小红还了解到三角形的内角和 , 同时她很容易地证明了三角形外角的性质,即三角形的一个外角等于与它不相邻的两个内角的和. 于是,爱思考的小红在想,三角形的内角是否也具有类似的性质呢?三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?小红利用类比思想开始了探究.
(1)、求证:;(2)、求证: .20. 小红在数学课上学习了角的相关知识后,立即对角产生了浓厚的兴趣.她查阅书籍发现两个有趣的概念,三角形中相邻两条边的夹角叫做三角形的内角;三角形一条边的延长线与其邻边的夹角,叫做三角形的外角.小红还了解到三角形的内角和 , 同时她很容易地证明了三角形外角的性质,即三角形的一个外角等于与它不相邻的两个内角的和. 于是,爱思考的小红在想,三角形的内角是否也具有类似的性质呢?三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?小红利用类比思想开始了探究.
尝试探究:
如图1,与分别为的两个外角,试探究与之间存在怎样的数量关系?为什么?
解:数量关系: .
理由:∵与分别为的两个外角,
∴ .
∴ .
∵三角形的内角和为 ,
∴ .
∴ .
小红顺利地完成了探究过程,并想考一考同学们,请同学们利用上述结论完成下面的问题.
(1)、初步应用:如图2,在纸片中剪去 , 得到四边形 , , 则=;
(2)、拓展提升:请聪明的你帮小红解决下列问题.
如图3,在中,分别平分外角 , 小红很容易推导出与的数量关系为 .
如图4,在四边形中,分别平分外角 , 则与有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由.)
四、实践探究题(共13分)
-
21. 如图
 (1)、【探究与发现】如图1,是的中线,延长至点E,使 , 连接 , 写出图中全等的两个三角形 .(2)、【理解与应用】填空:如图2,是的中线,若 , , 设 , 则x的取值范围是 .(3)、已知:如图3,是的中线, , 点Q在的延长线上, , 求证: .
(1)、【探究与发现】如图1,是的中线,延长至点E,使 , 连接 , 写出图中全等的两个三角形 .(2)、【理解与应用】填空:如图2,是的中线,若 , , 设 , 则x的取值范围是 .(3)、已知:如图3,是的中线, , 点Q在的延长线上, , 求证: .