人教版八年级上学期数学第十三章质量检测（高阶）

试卷更新日期：2024-09-26 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 在平面直角坐标系中，已知M(0，6)，△MON为等腰三角形且面积为9，满足条件的N点有（）

A、2个 B、4个 C、8个 D、10个

查看试题解析
2. 如图，在四边形 $A B C D ， D A ⊥ A B ， D A = 6 c m ， ∠ B + ∠ C = 150 ° ， A$ 刚好是 $E B$ 中点，P、Q分别是线段 $C E 、 B E$ 上的动点，则 $B P + P Q$ 的最小值为（）

A、12 B、15 C、16 D、18

查看试题解析
3. 平面直角坐标系中，已知A（2，0），B（0，2）若在坐标轴上取C点，使△ABC为等腰三角形，则满足条件的点C的个数是（）

A、4 B、6 C、7 D、8

查看试题解析
4. 如图， $∠ A O B = 3 0^{°} ， M 、 N$ 分别是边OA、OB上的定点，P、Q分别是边OB、OA上的动点，记 $∠ A M P$ $= ∠ 1 ， ∠ O N Q = ∠ 2$ ，当 $M P + P Q + Q N$ 最小时，则关于 $∠ 1 、 ∠ 2$ 的数量关系正确的是（）

A、 $∠ 1 + ∠ 2 = 9 0^{°}$ B、 $2 ∠ 1 + ∠ 2 = 18 0^{°}$ C、 $∠ 1 - ∠ 2 = 9 0^{°}$ D、 $2 ∠ 2 - ∠ 1 = 3 0^{°}$

查看试题解析
5. 如图，AD为等边△ABC的高，E、F分别为线段AD、AC上的动点，且AE＝CF，当BF＋CE取得最小值时，∠AFB＝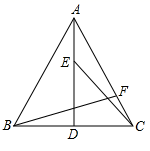

A、112.5° B、105° C、90° D、82.5°

查看试题解析
6. 如图，在 $△ A B C$ 中， $∠ A B C = 60 °$ ， $A D$ 平分 $∠ B A C$ 交 $B C$ 于点 $D ， C E$ 平分 $∠ A C B$ 交 $A B$ 于点 $E ， A D 、 C E$ 交于点 $F$ ．则下列说法正确的个数为（）
① $∠ A F C = 120 °$ ；② $S_{△ A B D} = S_{△ A D C}$ ， ③若 $A B = 2 A E$ ，则 $C E ⊥ A B$ ；④ $C D + A E = A C$ ；⑤ $S_{△ A E F} ： S_{△ F D C} = A F ： F C$ ．

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题（每题3分，共15分）

7. 如图，在等腰三角形 $△ A B C$ 中， $A B = A C$ ， D为 $B C$ 延长线上一点， $E C ⊥ A C$ 且 $A C = C E$ ，垂足为C ，连接 $B E$ ，若 $B C = 6$ ，则 $△ B C E$ 的面积为．

查看试题解析
8. 已知如图， $△ A B C$ 中， $A C = B C$ ， $A D$ 平分 $∠ B A C$ 交 $B C$ 于点D， $∠ B = a$ ，有以下结论：
①若 $a = 45 °$ ，则 $A B = A C + C D$ ；
②若 $a = 40 °$ ，则 $A B = A D + C D$ ；
③若 $a = 36 °$ ，则 $A B = A C + C D$ ；
④若 $a = 30 °$ 、则 $A B = A C + 2 C D$ ．
其中正确的有．

查看试题解析
9. 如图所示，已知△ABC中，∠ACB＝90°，∠BAC＝30°，BC＝1，作AC的垂直平分线交AB于点 $B_{1}^{}$ 、交AC于点 $C_{1}^{}$ ，连接 $B_{1}^{} C$ ，得到第一条线段 $B_{1}^{} C$ ；作 $A C_{1}^{}$ 的垂直平分线交AB于点 $B_{2}^{}$ 、交 $A C_{1}^{}$ 于点 $C_{2}^{}$ ，连接 $B_{2}^{} C_{1}^{}$ ，得到第二条线段 $B_{2}^{} C_{1}^{}$ ；作 $A C_{2}^{}$ 的垂直平分线交AB于点 $B_{3}^{}$ 、交 $A C_{2}^{}$ 于点 $C_{3}^{}$ ，连接 $B_{3}^{} C_{2}^{}$ ，得到第三条线段 $B_{3}^{} C_{2}^{}$ ；……如此作下去，则第n条线段 $B_{n}^{} C_{n - 1}^{}$ 的长为．

查看试题解析

三、解答题（共7题，共67分）

10.

(1)、如图1，点 $D$ 、 $E$ 分别是等边 $△ A B C$ 边 $A C$ 、 $A B$ 上的点，连接 $B D$ 、 $C E$ ，若 $A E = C D$ ，求证： $B D = C E$

(2)、如图2，在（1）问的条件下，点 $H$ 在 $B A$ 的延长线上，连接 $C H$ 交 $B D$ 延长线于点 $F$ ，．若 $B F = B C$ ，求证： $E H = E C$ ．

查看试题解析
11. 如图，BC⊥CA，BC＝CA，DC⊥CE，DC＝CE，直线BD与AE交于点F，交AC于点G，连接CF．

(1)、求证：△ACE≌△BCD；

(2)、求证：BF⊥AE；

(3)、请判断∠CFE与∠CAB的大小关系并说明理由．

查看试题解析
12. 在 $△ A B C$ 中， $∠ B = 60 °$ ， $D$ 是 $B C$ 上一点，且 $A D = A C$ ．

(1)、如图 $1$ ，延长 $B C$ 至 $E$ ，使 $C E = B D$ ，连接 $A E .$ 求证： $A B = A E$ ；

(2)、如图 $2$ ，在 $A B$ 边上取一点 $F$ ，使 $D F = D B$ ，求证： $A F = B C$ ；

(3)、如图 $3$ ，在（2）的条件下， $P$ 为 $B C$ 延长线上一点，连接 $P A$ ， $P F$ ，若 $P A = P F$ ，猜想 $P C$ 与 $B D$ 的数量关系并证明．

查看试题解析
13. 如图，在 $△ A B C$ 中， $C A = C B$ ，点 $D$ 是CB上一动点，点 $E$ 在AD的延长线上，且 $C A = C E$ ， $C F$ 平分 $∠ B C E$ 交DE于 $F$ ，连接BF．

(1)、如图1，求证： $∠ C A F = ∠ C B F$ ；

(2)、如图2， $∠ A B C = 60 °$ 时，求证： $C F + E F = A F$ ；

(3)、如图3，当 $∠ A B C = 45 °$ 时，过点 $A$ 作AB的垂线 $l$ ，过点 $C$ 作AB的平行线 $n$ ，两直线l，n相交于 $M$ ，连接ME．当ME取得最大值时，请直接写出此时 $\frac{E F}{A D}$ 的值．

查看试题解析
14. 在平面直角坐标系中，点O为坐标原点， $A (a, 0)$ ， $B (0, b)$ ，且a，b满足 ${(a - 4)}^{2} + |a - b| = 0$ ．

(1)、求点A、点B的坐标．

(2)、 $P (0, t)$ 为y轴上一动点，连接 $A P$ ，过点P在线段 $A P$ 上方作 $P M ⊥ P A$ ，且 $P M = P A$ ．
①如图1，若点P在y轴正半轴上，点M在第一象限，连接 $M B$ ，过点B作 $P M$ 的平行线交x轴于点R．求点R的坐标（用含t的式子表示）．
②如图2，连接 $O M$ ，探究当 $O M$ 取最小值时，线段 $O M$ 与 $A B$ 的关系．

查看试题解析
15. 在等边 $△ A B C$ 中，点 $E$ 为边 $A B$ 上任意一点，点 $D$ 在边 $C B$ 的延长线上，且 $E D = E C$ ．

(1)、如图1，若点 $E$ 为 $A B$ 的中点，求证： $A E = D B$ ；

(2)、如图2，若点 $E$ 为 $A B$ 上任意一点，求证： $A E = D B$ ．

查看试题解析

四、实践探究题（共8分）

16. 问题情境：
定义：如果两个等腰三角形的顶角互补，顶角的顶点又是同一个点，而且这两个等腰三角形的腰也分别相等，则称这两个三角形互为“顶补等腰三角形”．

(1)、特例证明：
如图1，若 $△ A B C$ 与 $△ A D E$ 互为“顶补等腰三角形”． $∠ B A C > 90 °$ ， $A M ⊥ B C$ 于 $M$ ， $A N ⊥ E D$ 于 $N$ ，求证： $N E = A M$ ；

(2)、拓展运用：
如图2，在四边形 $A B C D$ 中， $A D = A B$ ， $C D = B C$ ， $∠ B = 90 °$ ， $∠ A = 60 °$ ，在四边形 $A B C D$ 的内部是否存在点 $P$ ，使得 $△ P A B$ 与 $△ P D C$ 互为“顶补等腰三角形”？若存在，请给予证明；若不存在，请说明理由．

查看试题解析