人教版八年级上学期数学课时进阶测试13.4最短路径(三阶)
试卷更新日期:2024-09-26 类型:同步测试
一、选择题(3分)
-
1. 如图,∠AOB=30°,M、N分别是边OA、OB上的定点,P、Q分别是边OB、OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1、∠2的数量关系正确的是( )
 A、∠1+∠2=90° B、2∠1+∠2=180° C、∠1-∠2=90° D、2∠2-∠1=30°2. 如图,在四边形ABCD中,DA⊥AB . DA=6cm , ∠B+∠C=150°,CD与BA的延长线交于E点,A刚好是EB中点,P、Q分别是线段CE、BE上的动点,则BP+PQ最小值是( )
A、∠1+∠2=90° B、2∠1+∠2=180° C、∠1-∠2=90° D、2∠2-∠1=30°2. 如图,在四边形ABCD中,DA⊥AB . DA=6cm , ∠B+∠C=150°,CD与BA的延长线交于E点,A刚好是EB中点,P、Q分别是线段CE、BE上的动点,则BP+PQ最小值是( ) A、12 B、15 C、16 D、183. 如图,在平面直角坐标系中,点A的坐标为(4,0),点Q是直线yx上的一个动点,以AQ为边,在AQ的右侧作等边△APQ,使得点P落在第一象限,连接OP,则OP+AP的最小值为( )
A、12 B、15 C、16 D、183. 如图,在平面直角坐标系中,点A的坐标为(4,0),点Q是直线yx上的一个动点,以AQ为边,在AQ的右侧作等边△APQ,使得点P落在第一象限,连接OP,则OP+AP的最小值为( ) A、6 B、4 C、8 D、64. 如图,过边长为2的等边的顶点C作直线 , 然后作关于直线l对称的 , P为线段上一动点,连接 , , 则的最小值是( )
A、6 B、4 C、8 D、64. 如图,过边长为2的等边的顶点C作直线 , 然后作关于直线l对称的 , P为线段上一动点,连接 , , 则的最小值是( ) A、4 B、3 C、2 D、15. 如图.在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )
A、4 B、3 C、2 D、15. 如图.在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( ) A、84° B、88° C、90° D、96°6. 如图,中, , 垂足为 , 点为直线上方的一个动点,的面积等于的面积的 , 则当最小时,的度数为( )
A、84° B、88° C、90° D、96°6. 如图,中, , 垂足为 , 点为直线上方的一个动点,的面积等于的面积的 , 则当最小时,的度数为( )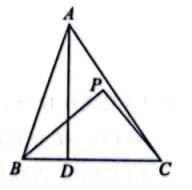 A、 B、 C、 D、7. 如图,在中, , , , , 动点P在边上,点P关于 , 的对称点分别为点E,F,连接 , 交 , 分别为点M,N.
A、 B、 C、 D、7. 如图,在中, , , , , 动点P在边上,点P关于 , 的对称点分别为点E,F,连接 , 交 , 分别为点M,N.甲:我发现线段的最大值为2,最小值为;
乙:我连接 , , 发现一定为钝角三角形.
则下列判断正确的是( )
 A、甲对乙对 B、甲对乙错 C、甲错乙对 D、甲错乙错8. 如图所示,在四边形ABCD中, , , , , 在AD上找一点P,使的值最小;则的最小值为( )
A、甲对乙对 B、甲对乙错 C、甲错乙对 D、甲错乙错8. 如图所示,在四边形ABCD中, , , , , 在AD上找一点P,使的值最小;则的最小值为( )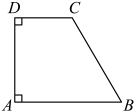 A、4 B、3 C、5 D、6
A、4 B、3 C、5 D、6二、填空题(3分)
-
9. 如图,边长为2的等边中,是边上的中线,点E在上,连接 , 在的下方作等边 , 连接 , 则周长的最小值是 .
 10. 如图,△ABC和△DCE都是边长为6的等边三角形,且点B、C、E在同一条直线上,点P是CD边上的一个动点,连接AP,BP,则AP+BP的最小值为.
10. 如图,△ABC和△DCE都是边长为6的等边三角形,且点B、C、E在同一条直线上,点P是CD边上的一个动点,连接AP,BP,则AP+BP的最小值为. 11. 点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是 轴上使得∣PA—PB∣的值最大的点,Q是y轴上使得QA+QB的值最小的点,则OP·OQ=.
11. 点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是 轴上使得∣PA—PB∣的值最大的点,Q是y轴上使得QA+QB的值最小的点,则OP·OQ=. 12. 如图,矩形ABCD中,AB=2,AD=3,点E、F分别AD、DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为 .
12. 如图,矩形ABCD中,AB=2,AD=3,点E、F分别AD、DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为 . 13. 如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 .
13. 如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 .
三、解答题

