人教版八年级上学期数学课时进阶测试13.4最短路径（二阶）
试卷更新日期：2024-09-26 类型：同步测试
一、选择题（3分）
-
1. 如图，点N在等边△ABC的边BC上，CN＝6，射线BD⊥BC ， 垂足为点B ， 点P是射线BD上一动点，点M是线段AC上一动点，当MP+NP的值最小时，CM＝7，则AC的长为（ ）
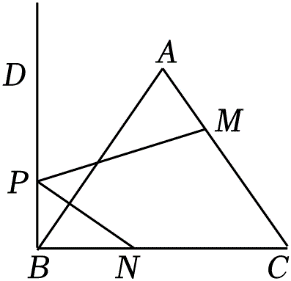A、8 B、9 C、10 D、122. 如图，在△ABC中，∠C=90°，∠BAC=30°，AB=12，AD平分∠BAC，点PQ分别是AB、AD边上的动点，则BQ+QP的最小值是（ ）
A、4 B、5 C、6 D、73. 如图，四边形ABCD中，∠A＝∠C＝90°，点M、N分别是BC、AB边上的动点，∠B＝56°，当△DMN的周长最小值时，则∠MDN的度数是（ ）
A、124° B、68° C、60° D、56°4. 如图，P是∠AOB内任意一点，OP=8 cm，M和N分别是射线OA和射线OB上的动点，△PMN周长的最小值是8cm，则∠AOB的度数是（ ）
A、30° B、40° C、50° D、60°5. 如图，在Rt△ABC中，∠ACB＝90°， AC=6， BC＝8，AB＝10， AD是∠BAC的平分线．若P ， Q分别是AD和AC上的动点，则PC+PQ的最小值是（ ）
A、2.4 B、4.8 C、4 D、56. 如图，在△ABC中，∠ACB=90°，以AC为底边在△ABC外作等腰△ACD，过点D作∠ADC的平分线分别交AB，AC于点E，F．若BC=7，∠CAB=30°，点P是直线DE上的一个动点，则△PBC周长的最小值为（ ）
A、20 B、 C、21 D、7. 已知 ， 在内有一定点P ， 点M ， N分别是上的动点，若的周长最小值为3，则的长为（ ）
A、1.5 B、3 C、2 D、2.58. 如图，等边和等腰 ， ， 点E，F分别为边 ， 的中点，若的面积为16， ， 点M是CE上的动点，则的周长的最小值为（ ）
A、6 B、8 C、9 D、10二、填空题（3分）
-
9. 如图，在四边形中， ， ， 在 ， 上分别找一个点M ， N ， 使的周长最小，则°
10. 如图，将一副直角三角尺ABC、ABD斜边重合按如图位置放置，其中 ，
⑴°；
⑵点E、F分别是边BC、BD上的点，连接AE、AF、EF ． 当周长最小时，°．
11. 如图所示∠AOB=60°，点Р是∠AOB内一定点，并且OP=2，点M、N分别是射线OA，OB上异于点O的动点，当△PMN的周长取最小值时，点О到线段MN的距离为.
12. 如图，在△ABC中，∠ACB＝90°，∠A＝30°，边AC的垂直平分线DE分别交边AB、AC于点D、E、P为直线DE上一点．若BC＝2，则△BCP周长的最小值为 ．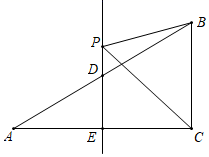
13. 如图，中， ， ， ， 平分 ， 如果点P，点G分别为 ， 上的动点，那么的最小值是.
三、解答题
