【提升版】北师大版数学九年级上册第三章 概率的进一步认识 章节测试卷
试卷更新日期：2024-09-25 类型：单元试卷
一、选择题（每题3分，共24分）
-
1. 中国古代的“四书”是指《论语》《孟子》《大学》《中庸》，它是儒家思想的核心著作，是中国传统文化的重要组成部分.若从这四部著作中随机抽取两本（先随机抽取一本，不放回，再随机抽取另一本），则抽取的两本恰好是《论语》和《大学》的概率是（ ）
A、 B、 C、 D、2. 数学课上，李老师与学生们做“用频率估计概率”的试验：不透明袋子中有5个白球、3个红球和2个黄球，这些球除颜色外无其他差别．从袋子中随机取出一个球，某种颜色的球出现的频率如图所示，则该球的颜色最有可能是（ ）
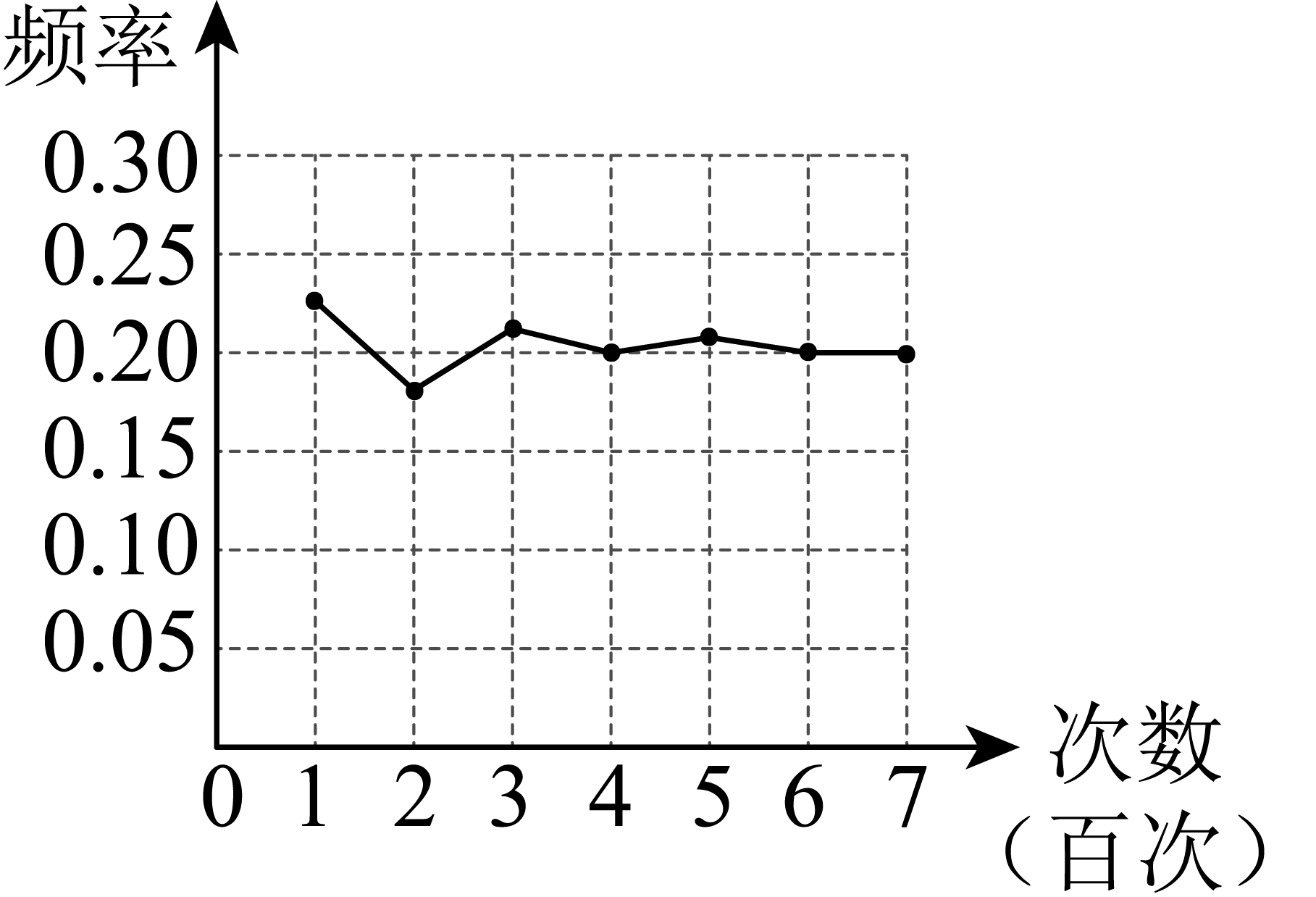A、黑球 B、黄球 C、红球 D、白球3. 随机抛掷一枚瓶盖1000次，经过统计得到“正面朝上”的次数为420次，则可以由此估计抛掷这枚瓶盖出现“反面朝上”的概率为（ ）A、0.22 B、0.42 C、0.50 D、0.584. 在一个不透明的盒子中装有n个小球，它们除了颜色不同外，其余都相同，其中有4个白球，每次试验前，将盒子中的小球摇匀，随机摸出一个球记下颜色后再放回盒中．大量重复上述试验后发现，摸到白球的频率稳定在0.4，那么可以推算出n大约是（ ）A、10 B、14 C、16 D、405. 为了估计水塘中的鱼数，养鱼者先从鱼塘中捕获30条鱼，在每一条鱼身上做好标记后把这些鱼放归鱼塘，再从鱼塘中打捞鱼．通过多次实验后发现捕捞的鱼中有作记号的频率稳定在2.5%左右，则鱼塘中鱼的条数估计为（ ）A、600条 B、1200条 C、2200条 D、3000条6.如图，现分别旋转两个标准的转盘，则转盘所转到的两个数字之积为奇数的概率是（ ）
A、 B、 C、 D、7. 如图所示，电路图上有四个开关A，B，C，D和一个小灯泡，闭合开关D或同时闭合开关A，B，C都可使小灯泡发光，则任意闭合其中两个开关，小灯泡发光的概率是（ ）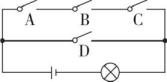
A、 B、 C、 D、8. 某轨道列车共有3节车厢，设旅客从任意一节车厢上车的机会均等，某天，甲、乙两位乘客同时乘一列轨道列车，则甲和乙从同一节车厢上车的概率是（ ）A、 B、 C、 D、二、填空题（每题3分，共15分）
-
9. 将分别标有“醉”“美”“贵”“州”四个汉字的小球装在一个不透明的口袋中，这些小球除汉字以外其他完全相同，每次摸球前先搅匀，随机摸出一球，不放回，再随机摸出一球，两次摸出的球上的汉字能组成“贵州”的概率是 ．10. 在一个不透明的袋子中，有白色棋子和黑色棋子共20颗，这些棋子除颜色外均相同，将袋中的棋子搅匀，从中随机摸出一颗棋子，记下颜色后再放回袋子中，不断重复这一过程，摸了100次后，发现有60次摸到黑色棋子，请你估计这个袋子中黑色棋子有颗．11. 某学习小组做“用频率估计概率”的摸球试验：在不透明的盒子中装入红色、蓝色的玻璃球共个，从中随机摸出一个球，记下颜色后放回，统计了“摸出球为红色”出现的频率，绘制了如图的折线统计图，那么估计盒子中装入红色球的个数约为 ．
12. 连续投掷两枚质地均匀的硬币，两枚硬币恰好是一正一反的概率是
13. 现有四张正面分别标有数字﹣1，1，2，3的不透明卡片，它们除数字外其余完全相同，将它们背而面朝上洗均匀，随机抽取一张，记下数字后放回 ， 背面朝上洗均匀，再随机抽取一张记下数字，前后两次抽取的数字分别记为m ， n ， 则点P（m ， n）在第二象限的概率为 ．三、解答题（共7题，共61分）
-
14. “校园安全”受到全社会的广泛关注，我市某中学对部分学生就校园安全知识的了解程度进行了随机抽样调查（被调查学生必选且仅选一项），并根据收集到的信息绘制了下面两幅尚不完整的统计图请你根据统计图中所提供的信息，解答下列问题：
(1)、请把条形统计图补充完整（需写出计算过程）；(2)、若从对校园安全知识达到“基本了解”程度的3名女生和2名男生中，随机抽取2人参加校园安全知识竞赛，请用画树状图或列表的方法，求出恰好抽到1名男生和1名女生的概率．15. 甲、乙两个盒子中装有质地、大小相同的小球，甲盒中有2个白球、1个黄球和1个蓝球；乙盒中有1个白球、2个黄球和若干个蓝球．从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍．(1)、求乙盒中蓝球的个数．(2)、从甲、乙两盒中分别任意摸取一球，利用列表或画树状图法求这两球均为蓝球的概率．16. 太阳发出的光经过三棱镜折射后，可以形成红、橙、黄、绿、蓝、靛、紫等色光组成的光带，这是光的色散现象，说明太阳发出的白光是由不同色光组成的．自然界大部分彩色的光都可以通过红、绿、蓝三种颜色的光按照不同比例混合而成，所以这三种色光又被称为光的“三原色”．在一次数学课上，老师利用光的三原色设计了一个“配紫色”游戏，如图所示是一个可以自由转动的转盘，转盘被分成面积相等的三个扇形，分别对应红、绿、蓝三种颜色，转动转盘2次，记下两次指针指向的区域（若指针指向扇形分界线，则需要重新转动），如果转出的两种颜色分别是红色和蓝色，则可以配成紫色．
(1)、用列表或画树状图的方法表示出所有可能出现的结果；(2)、求转动2次转盘，恰好可以配成紫色的概率．17. 如图，某同学学习物理电流和电路后，设计了如图所示的电路图，其中、、、分别表示四个可开闭的开关，“”表示小灯泡，“
”表示电源.电源、小灯泡、开关和线路都能正常工作，当闭合开关、、中任意一个，再闭合开关时，小灯泡发光，按要求完成下列问题：
(1)、当开关闭合时，再随机闭合开关或或其中的一个，小灯泡发光的概率为；(2)、当随机闭合开关、、、中的两个，请用画树状图或列表的方法求小灯泡发光的概率.18. 为大力弘扬“奉献、友爱、互助、进步”的志愿精神，我市某社区开展了“文明新风进社区”系列志愿服务活动，参加活动的每位志愿者必须从A ． “垃圾分类入户宣传”、B ． “消防安全知识宣传”、C ． “走访慰问孤寡老人”、D ． “社区环境整治活动”四个活动主题中随机选取一个主题中随机选取一个主题．(1)、志愿者小李选取A ． “垃圾分类入户宣传”这个主题的概率是 ．(2)、志愿者小张和小李从A、B、C、D四个主题中分别随机选取一个主题，请用列表或画树状图的方法，求他们选取相同主题的概率．19. 某校计划举办“学习二十大”演讲比赛，确定了“5G时代”、“北斗卫星”、“高铁速度”、“绿色低碳”四个主题，将其制成四张背面看上去无差别的卡片（如图所示），并把卡片背面朝上洗匀．
(1)、若小丽随机抽取一张卡片，则她选中的主题是“绿色低碳”的概率是；(2)、若小英从卡片中随机抽取一张卡片确定主题后，将卡片放回洗匀，小亮再随机从中抽取一张卡片确定主题，请用列表或画树状图的方法求出他们恰好抽取不同主题的概率．（用对应的字母表示）20. 2023年国际乒联混合团体世界杯于2023年12月4日在成都举行，本次赛会的会徽彰显了成都文化特色，吉祥物“乒乒”将大熊猫与乒乓球运动相结合，表达了成都人民对乒乓球运动的喜爱．现有三张不透明的卡片，其中一张卡片的正面图案为会徽，另外两张卡片的正面图案都为吉祥物“乒乒”，卡片除正面图案不同外其余均相同，将这三张卡片背面向上并搅匀．
(1)、小明从中随机抽取一张，“抽到卡片上的图案是会徽”是事件（填“随机”“不可能”或“必然”）；(2)、小亮从中随机抽取一张，记下卡片上的图案后背面向上放回，重新搅匀后再从中随机抽取一张．请用画树状图（或列表）的方法，求小亮两次抽到的卡片上的图案都是吉祥物“乒乒”的概率．（图案为会徽的卡片记为 ， 图案为吉祥物的两张卡片分别记为、）