【基础版】北师大版数学九年级上册第三章 概率的进一步认识 章节测试卷
试卷更新日期：2024-09-25 类型：单元试卷
一、选择题（每题3分，共24分）
-
1. 一个家庭有两个孩子，两个都是女孩的概率是（ ）A、 B、 C、 D、无法确定2. 有两辆车按1，2编号，方方和成成两人可以任意选坐一辆车，则两人同坐1号车的概率为（ ）A、 B、 C、 D、3. 一个不透明的箱子里装有m个球，其中红球3个，这些球除颜色不同其余都相同，每次搅拌均匀后，任意摸出一个球记下颜色后再放回，大量重复试验发现，摸到红球的频率稳定在0.3附近，则可以估算出m的值为（ ）A、3 B、5 C、10 D、124. 在一个不透明的布袋中装有50个黄、白两种颜色的球，除颜色外其他都相同，小红通过多次摸球试验后发现，摸到黄球的频率稳定在左右，则布袋中黄球可能有（ ）A、40个 B、35个 C、25个 D、15个5. 在一个不透明的口袋里，装了只有颜色不同的黄球、白球若干只.某小组做摸球试验：将球搅匀后从中随机摸出一个，记下颜色，再放回袋中，不断重复.下表是活动中的一组数据，则摸到黄球的概率约是（ ）
摸球的
次数n
100
150
200
500
800
1 000
摸到黄球
的次数m
52
69
96
266
393
507
摸到黄球
的频率
0.52
0.46
0.48
0.532
0.491
0.507
A、0.4 B、0.5 C、0.6 D、0.76. 二维码越来越普及到人们生活的方方面面，成为了广大民众生活中不可或缺的一部分.如图是小刚在面积为16的正方形纸片上打印的二维码，为了估计黑色阴影部分的面积，他在纸内随机掷点，经过大量实验，发现点落在黑色阴影的频率稳定在0.6左右，则据此估计此二维码中黑色阴影的面积为（ ）
A、9.6 B、0.6 C、6.4 D、0.47. 将分别标有“大”、“美”、“明”、“德”四个汉字的小球装在一个不透明的口袋中，这些小球除汉字以外其它完全相同，每次摸球前先搅匀，随机摸出一球，不放回，再随机摸出一球，两次摸出的球上的汉字可以组成“明德”的概率是（ ）A、 B、 C、 D、8. 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如下的表格，则符合这一结果的实验最有可能的是（ ）实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A、一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃 B、抛一个质地均匀的正六面体骰子，向上的面点数是5 C、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀” D、抛一枚硬币，出现反面的概率二、填空题（每题3分，共15分）
-
9. 不透明布袋中有红、黄小球各一个，除颜色外无其他差别．随机摸出一个小球后，放回并摇匀．再随机摸出一个，一个红球、一个黄球的概率为10. 某批青稞种子在相同条件下发芽试验结果如下表：
每次试验粒数
50
100
300
400
600
1000
发芽频数
47
96
284
380
571
948
估计这批青稞发芽的概率是.（结果保留到0.01）
11. 某试验小组做了可转动转盘（如图），想求当转盘停止转动后，“指针落在灰色区域内”的概率，试验数据如下表：试验次数n
20
40
60
80
100
1000
“指针落在灰色区域内”的次数m
6
11
15
21
25
251
“指针落在灰色区域内”的频率
0.3
0.275
0.25
0.2625
0.25
0.251
根据表格，可以估计出转动转盘一次，当转盘停止转动后，“指针落在灰色区域内”的概率约是 ． （结果精确到0.01）
12. 小明与父母从广州乘火车回梅州参观叶帅纪念馆，他们买到的火车票是同一排相邻的三个座位，那么小明恰好坐在父母中间的概率是.13. 在一个不透明的袋子里装有若干个白球和6个黄球，这些球除颜色不同外其余均相同，每次从袋子中摸出一个球记录下颜色后再放回，经过很多次重复试验，发现摸到黄球的频率稳定在0.75，则袋中白球有个；三、解答题（共7题，共61分）
-
14. 临近毕业，甲、乙、丙三人相约去餐馆聚餐，丙先到达餐馆，选了一张方桌坐在如图所示的座位上，甲到达餐馆后，从座位①、②、③中随机选择一个坐下，乙到达餐馆后，从剩下的座位中再随机选择一个坐下．
(1)、甲坐在①号座位上的概率是；(2)、用列表法或画树状图的方法，求甲、乙两人恰好相邻而坐的概率．15. 一个不透明的袋子中装有2个红球和1个白球（只有颜色不同），从中随机摸出1个球后放回搅匀，再次随机摸出一个球，请用列表或画树状图的方法求先后摸出的两球颜色不同的概率.16. 将如图所示的牌面数字分别是1，2，3，4的四张扑克牌背面朝上，洗匀后放在桌面上．
(1)、从中随机抽出一张牌，牌面数字小于3的概率是；(2)、先从中随机抽出一张牌不放回，将牌面数字作为十位上的数字，然后再随机抽取一张，将牌面数字作为个位上的数字，请用画树状图或列表的方法求组成的两位数恰好是3的倍数的概率．17. 在一个箱子里放着分别标有数字1，2，3的三个球，它们除了号码外其他都相同．(1)、从箱子里摸出一个球，有几种不同的可能？(2)、从箱子里随机摸出两个球(先摸出一个，不放回，再摸出一个)，这样按顺序先后摸得的两个球有几种不同的可能？(3)、从箱子里随机摸出一个球，放回，摇匀后再摸出一个球，这样按顺序先后摸得的两球有几种不同的可能？(画树状图或列表分析问题)18. 现有三位“抗疫”英雄（依次标记为A，B，C）．为了让同学们了解他们的英雄事迹，张老师设计了如下活动：取三张完全相同的卡片，分别在正面写上A，B，C三个标号，然后背面朝上放置，搅匀后请一位同学从中随机抽取一张，记下标号后放回，要求大家依据抽到标号所对应的人物查找相应“抗疫”英雄资料.(1)、求班长在这三种卡片中随机抽到标号为C的概率；(2)、用树状图或列表法求小明和小亮两位同学抽到的卡片是不同“抗疫”英雄标号的概率.19. 如图，3×3的方格分为上中下三层，第一层有一枚黑色方块甲，可在方格A、B、C中移动，第二层有两枚固定不动的黑色方块，第三层有一枚黑色方块乙，可在方格D、E、F中移动，甲、乙移入方格后，四枚黑色方块构成各种拼图．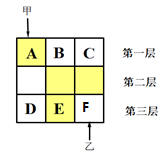
(1)、若乙固定在E处，移动甲后黑色方块构成的拼图是轴对称图形的概率是多少；(2)、若甲、乙均可在本层移动，用画树状图法或列表法求出黑色方块所构成拼图是轴对称图形的概率．20. 端午节吃粽子是中华民族的传统习俗，五月初五早上，奶奶为小明准备了四只粽子：一只肉馅，一只香肠馅，两只红枣馅，四只粽子除内部馅料不同外其他均一切相同．小明喜欢吃红枣馅的粽子．(1)、请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率；(2)、在吃粽子之前，小明准备用一个均匀的正四面体骰子（如图所示）进行吃粽子的模拟试验，规定：掷得点数1向上代表肉馅，点数2向上代表香肠馅，点数3，4向上代表红枣馅，连续抛掷这个骰子两次表示随机吃两只粽子，从而估计吃两只粽子刚好都是红枣馅的概率．你认为这样模拟正确吗？试说明理由．
