【提升版】北师大版数学九年级上册3.2用频率估计概率同步练习

试卷更新日期：2024-09-24 类型：同步测试

进入出卷网下载

一、选择题

1. 某数学兴趣小组做“用频率估计概率”的试验时，统计了某结果出现的频率，绘制了如下的表格，则符合这一结果的试验最有可能是
试验总次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333

A、掷一枚质地均匀的硬币，出现反面朝上 B、掷一枚质地均匀的骰子，掷得朝上的点数是5 C、在“石头、剪刀、布”游戏中，小明出的是“剪刀” D、将一副去掉大小王的普通扑克牌洗匀后，从中任抽一张扑克牌的花色是红桃

查看试题解析
2. 在一个不透明的盒子里装有若干个白球和15个红球，这些球除颜色不同外其余均相同，每次从袋子中摸出一个球记录下颜色后再放回，经过多次重复试验，发现摸到白球的频率稳定在0.4左右，则袋中白球约有（　　）

A、5个 B、10个 C、15个 D、25个

查看试题解析
3. 种子被称作农业的“芯片”，关系到国家粮食安全．某种业公司培育成功了 $A ， B$ 两种新玉米种子，为了了解它们的出芽情况，在推广前做了五次出芽实验，每次随机各自取相同种子数，在相同的培有环境中分别实验，实验情况记录如下：
种子数量 200 500 800 1500 3000
A 出芽率 0.98 0.94 0.96 0.98 0.97
B 出芽率 0.98 0.95 0.94 0.97 0.96
下面在三个推断：
①当实验种子数员为200时，两种种子的出芽率均为0.98，所以 $A ， B$ 两种新五米种子出芽的概率一样；
②随着实验种子数量的增加， $B$ 种子出芽率在0.96附近摆动，显示出一定的稳定性，可以估计 $B$ 种子出芽的概率是0.96：
③在同样的地质环境下播种， $A$ 种子的出芽率可能会离于 $B$ 种子．
其中合理的是（）

A、①②③ B、①② C、②③ D、①③

查看试题解析
4. 下列说法中，正确的是（）

A、通过少量重复试验，可以用频率估计概率 B、事件发生的可能性越大，它的概率越接近1 C、某种彩票中奖的概率是 $1 %$ ，因此买100张该种彩票就一定会中奖 D、概率很小的事件不可能发生

查看试题解析
5. 一个不透明的盒子里有n个除颜色外其它完全相同的小球，其中有6个黄球．每次摸球前先将盒子里的球摇匀，任意摸出一个球记下颜色后在放回盒子，通过大量重复摸球实验后发现，摸到黄球的频率稳定在30%，那么可以推算出n大约是( )

A、6 B、10 C、18 D、20

查看试题解析
6. 为了估计湖里有多少条鱼，小刚先从湖里捞出了100条鱼做上标记，然后放回湖里去．经过一段时间，带有标记的鱼完全混合于鱼群后，小刚又从湖里捞出200条鱼，如果其中15条有标记，那么估计湖里有鱼（）

A、1333条 B、3000条 C、300条 D、1500条

查看试题解析
7. 在一个不透明的布袋中装有50个黄、白两种颜色的球，除颜色外其他都相同，小红通过多次摸球试验后发现，摸到黄球的频率稳定在0.3左右，则布袋中白球可能有（　　）

A、40个 B、35个 C、20个 D、15个

查看试题解析
8. 绿豆在相同条件下的发芽试验，结果如表所示：
每批
粒数n
100
300
400
600
1 000
2 000
3 000
发芽的
粒数m
96
282
382
570
948
1 904
2 850
发芽的
频率 $\frac{m}{n}$
0.960
0.940
0.955
0.950
0.948
0.952
0.950
下面有三个推断：
①当n=400时，绿豆发芽的频率为0.955，所以绿豆发芽的概率是0.955；
②根据上表，估计绿豆发芽的概率是0.95；
③若n为4 000，估计绿豆发芽的粒数为 3 800 粒.
其中推断合理的是（）

A、① B、①② C、①③ D、②③

查看试题解析

二、填空题

9. 一个袋子中只装有红、白两种颜色的球，这些球的形状、质地等完全相同，其中白色球有3个，红色球有n个．在看不到球的条件下，随机地从袋子中摸出一个球，记录下颜色后，放回袋子中并摇匀．同学们进行了大量重复试验，发现摸出白球的频率稳定在 $0.2$ 附近，则n的值约为．

查看试题解析
10. 玉米是山西省主要农作物之一.某种业公司在选育玉米种子时，在同一条件下对某个品种的玉米种子进行了发芽试验，统计数据如下表：
试验种子粒数
100
200
500
1000
2000
5000
发芽种子粒数
92
188
476
951
1900
4752
据此估计该品种的玉米种子发芽的概率为.（结果精确到0.01）

查看试题解析
11. 如图，是一个面积为 $4 c m^{2}$ 正方形微信二维码．小明利用所学概率知识估算二维码中黑色部分的面积，在正方形区域内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在 $0.7$ 左右，据此可估计黑色部分的面积约为．

查看试题解析
12. 一年之计在于春，为保障春播任务顺利完成，科研人员对某玉米种子在相同条件下发芽情况进行试验，结果如表：
每批粒数n
500
800
1000
2000
3000
发芽的频数m
463
768
948
1901
2851
发芽的频率 $\frac{m}{n}$
0.926
0.96
0.948
0.951
0.950
那么这种玉米发芽的概率是．（结果精确到0.01）

查看试题解析
13. 如图，一张纸片上有一个不规则的图案（图中的小兔子），小雅想知道该图案的面积是多少，她采取了以下的办法：用一个长为 $10 c m$ ，宽为 $6 c m$ 的长方形将该图案围起来，然后在适当位置随机地向长方形区域内掷点，通过大量重复试验，发现点落在图案部分的频率稳定在0.6左右，由此她估计此不规则图案的面积大约为 $c m^{2}$ .

查看试题解析

三、解答题

14. 在一个不透明的袋子中装有红、黄两种颜色的球共20个，每个球除颜色外完全相同．某学习兴趣小组做摸球实验，将球搅匀后从中随机摸出1个球，记下颜色后再放回袋中，不断重复．下表是活动进行中的部分统计数据．
摸球的次数n
100
150
200
500
800
1000
摸到红球的次数m
59
96
118
290
480
601
摸到红球的频率 $\frac{m}{n}$
0.59
　
0.58

0.60
0.601
（1）完成上表；
（2）“摸到红球”的概率的估计值　（精确到0.1）
（3）试估算袋子中红球的个数．

查看试题解析
15. 一粒木质中国象棋子“兵”，它的正面雕刻一个“兵”字，它的反面是平的.将它从一定高度下掷，落地反弹后可能是“兵”字面朝上，也可能是“兵”字面朝下.由于棋子的两面不均匀，为了估计“兵”字面朝上的概率，某试验小组做了棋子下掷试验，试验数据如下表：
试验次数
20
40
60
80
100
120
140
160
“兵”字面
朝上频数
14
a
38
47
52
66
78
88
相应频率
0.7
0.45
0.63
0.59
0.52
b
0.56
0.55

(1)、请直接写出a，b的值.

(2)、如果试验继续进行下去，根据上表的数据，这个试验的频率将稳定在它的概率附近，请你估计这个概率是多少.

(3)、如果做这种试验2000次，那么“兵”字面朝上的次数大约是多少?

查看试题解析
16. 为弘扬中华传统文化，学校准备开展“国学知识挑战赛”．张老师将7张写有“成语故事”和若干张写有“国学常识”的卡片放入一个不透明的盒子中，这些卡片除上面的字外，其余完全相同．九年级学生想知道盒子中“国学常识”的张数，于是他们将卡片搅匀后从中任意摸出1张卡片，记下卡片上面的字后放回，搅匀后再摸一张卡片，记下卡片上面的字后放回，不断重复上述过程，获得数据如表：
摸卡次数
50
100
150
200
250
300
摸到“国学常识”的次数
17
29
46
59
74
90
摸到“国学常识”的频率
0.340
0.290
0.307
a
0.296
0.300

(1)、a＝，估计摸到“国学常识”的概率为（保留两位小数）；

(2)、根据表中数据，请你帮九年级学生估计盒子中有多少张“国学常识”卡片？

查看试题解析
17. 在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个，小明做摸球试验，他将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是试验中的一组统计数据：
摸球的
次数n
100
200
300
500
800
1 000
3 000
摸到白球
的次数m
70
128
171
302
481
599
1 806
摸到白球
的频率 $\frac{m}{n}$
0.7
0.64
0.57
0.604
0.601
0.599
0.602

(1)、请估计当n很大时，摸到白球的概率为(精确到0.1).

(2)、估算盒子里有白球个.

(3)、若向盒子里再放入x个除颜色以外其他完全相同的球，这x个球中白球只有1个，每次将球搅拌均匀后，任意摸出一个球记下颜色再放回，通过大量重复摸球试验后发现，摸到白球的频率稳定在 0.5，那么可以推测出x最有可能是多少?

查看试题解析
18. 小明在操场上玩游戏，他发现地上有一个不规则的封闭图形ABC.为了知道它的面积，小明在封闭图形内画出了一个半径为1m的圆，在不远处向圈内掷石子，且记录如下：

掷石子次数
50
150
300
石子落在 $⊙ o$ 内(含 $⊙ o$ 上)的次数m
14
43
93
石子落在阴影内的次数n
19
85
186
请你帮小明估计，此封闭图形ABC的面积是 $m^{2}$ .

查看试题解析
19. 某活动小组为了估计装有5个白球和若干个红球（每个球除颜色外都相同）的袋中红球约有多少个，在不将袋中球倒出来的情况下，分小组进行摸球试验，两人一组，共20组进行摸球试验，另一位学生记录所摸球的颜色，并将球放回袋中摇匀，每一组做400次试验，汇总起来后，摸到红球的次数为6000次。

(1)、估计从袋中任意摸出一个球，恰好是红球的概率是多少；

(2)、请你估计袋中红球有多少个。

查看试题解析

20. 某区规定学生每天户外体育活动时间不少于1小时．为了解学生参加户外体育活动的情况，对部分学生每天参加户外体育活动的时间进行了随机抽样调查，并将调查结果绘制成如下的统计表（不完整）．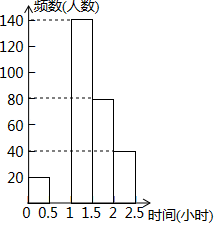

组别	时间（小时）	频数（人数）	频率
A	0≤t＜0.5	20	0.05
B	0.5≤t＜1	a	0.3
C	1≤t＜1.5	140	0.35
D	1.5≤t＜2	80	0.2
E	2≤t＜2.5	40	0.1

请根据图表中的信息，解答下列问题：

(1)、表中的a= ，将频数分布直方图补全；

(2)、该区8000名学生中，每天户外体育活动的时间不足1小时的学生大约有多少名？

(3)、若从参加户外体育活动时间最长的3名男生和1名女生中随机抽取两名，请用画树状图或列表法求恰好抽到1名男生和1名女生的概率．

查看试题解析

试验总次数	100	200	300	500	800	1000	2000
频率	0.365	0.328	0.330	0.334	0.336	0.332	0.333

种子数量		200	500	800	1500	3000
A	出芽率	0.98	0.94	0.96	0.98	0.97
B	出芽率	0.98	0.95	0.94	0.97	0.96

试验种子粒数	100	200	500	1000	2000	5000
发芽种子粒数	92	188	476	951	1900	4752

每批粒数n	500	800	1000	2000	3000
发芽的频数m	463	768	948	1901	2851
发芽的频率 $\frac{m}{n}$	0.926	0.96	0.948	0.951	0.950

摸球的次数n	100	150	200	500	800	1000
摸到红球的次数m	59	96	118	290	480	601
摸到红球的频率 $\frac{m}{n}$	0.59		0.58		0.60	0.601

摸卡次数	50	100	150	200	250	300
摸到“国学常识”的次数	17	29	46	59	74	90
摸到“国学常识”的频率	0.340	0.290	0.307	a	0.296	0.300

掷石子次数	50	150	300
石子落在 $⊙ o$ 内(含 $⊙ o$ 上)的次数m	14	43	93
石子落在阴影内的次数n	19	85	186

【提升版】北师大版数学九年级上册3.2用频率估计概率 同步练习

一、选择题

二、填空题

三、解答题

【提升版】北师大版数学九年级上册3.2用频率估计概率同步练习