【基础版】北师大版数学九年级上册3.2用频率估计概率同步练习

试卷更新日期：2024-09-24 类型：同步测试

进入出卷网下载

一、选择题

1. 小明练习射击，共射击60次，其中有38次击中靶子，由此可估计，小明射击一次击中靶子的概率是（　　）.

A、38% B、60% C、约63% D、无法确定

查看试题解析
2. 在大量重复试验中，关于随机事件发生的频率与概率，下列说法正确的是( )

A、频率就是概率 B、频率与试验次数无关 C、概率是随机的，与频率无关 D、随着试验次数的增加，频率一般会越来越接近概率

查看试题解析
3. 近几年，二维码逐渐进入了人们的生活，成为广大民众生活中不可或缺的一部分，小刚将二维码打印在面积为20的正方形纸片上，如图，为了估计黑色阴影部分的面积，他在纸内随机掷点，经过大量重复实验，发现点落在黑色阴影的频率稳定在 $0.6$ 左右，则据此估计此二维码中黑色阴影的面积为（）

A、8 B、12 C、 $0.4$ D、 $0.6$

查看试题解析

4. 某班的一个数学兴趣小组为了考察本市某条斑马线上驾驶员礼让行人的情况，每天利用放学时间进行调查，下表是该小组一个月内累计调查的结果，由此结果可估计驾驶员能主动给行人让路的概率为（）

抽查车辆数	100	500	1000	2000	3000	4000
能礼让的驾驶员人数	95	486	968	1940	2907	3880
能礼让的频率	0.95	0.972	0.968	0.97	0.969	0.97

A、0.95 B、0.96 C、0.97 D、0.98

查看试题解析

5. 某人在做抛掷硬币试验中，抛掷n次，正面朝上有m次，若正面朝上的频率是P＝ $\frac{m}{n}$ ，则下列说法正确的是（）

A、P一定等于0.5 B、多投一次，P更接近0.5 C、P一定不等于0.5 D、投掷次数逐渐增加，P稳定在0.5附近

查看试题解析
6. 一个盒子中装有a个白球和3个红球（除颜色外完全相同），若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子，通过大量重复试验后，发现摸到白球的频率稳定在80%左右，则a的值约为（）

A、9 B、12 C、15 D、18

查看试题解析
7. 如图所示，这是一幅长方形宣传画，长为4 m，宽为2 m.为测量画上图案的面积，现将宣传画平铺在地上，向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的)，经过大量重复投掷试验，发现骰子落在图案中的频率稳定在常数0.4左右.由此可估计宣传画上图案的面积为（）

A、2.4 m² B、3.2 m² C、4.8 m² D、7.2 m²

查看试题解析
8. 甲、乙两名同学在一次用频率去估计概率的实验中，统计了某一结果出现的频率，绘出的统计图如图所示，则符合这一结果的实验可能是（）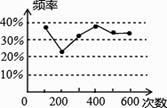

A、掷一枚质地均匀的正六面体的骰子，向上的一面点数是1点的概率 B、抛一枚质地均匀的硬币，出现正面朝上的概率 C、一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃的概率 D、在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”的概率

查看试题解析

二、填空题

9. 某学习小组做抛掷一枚瓶盖的实验，整理的实验数据如表：
累计抛掷次数
50
100
200
300
500
1000
2000
3000
5000
盖面朝上次数
28
54
106
158
264
527
1056
1587
2650
盖面朝上频率
0.5600
0.5400
0.5300
0.5267
0.5280
0.5270
0.5280
0.5290
0.530
随着实验次数的增大，“盖面朝上”的概率接近于（精确到0.01）．

查看试题解析
10. 某林业局将一种树苗移植成活的情况绘制成如图所示的折线统计图，由此可估计这种树苗移植成活的概率约为（精确到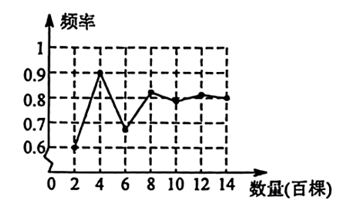 $0.1$ ）

查看试题解析
11. 某射击运动员封闭训练 $10$ 个月，每天击中 $9$ 环以上的频率记录如图，封闭训练结束时，估计这名运动员射击一次时“击中 $9$ 环以上”的概率为 $($ 结果保留一位小数 $)$ ．

查看试题解析
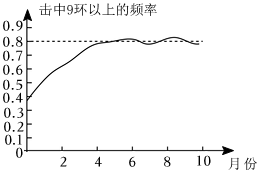12. 一个不透明的袋子中装有若干个白球和3个黄球，这些球除颜色外均相同．经多次摸球试验后发现，摸到黄球的频率稳定在 $0.25$ 左右，则袋子中白球的个数约为．

查看试题解析
13. 利用电脑程序模拟频率估计概率，在如图所示的同心圆中，大圆的半径为3，向大圆中（不含边界）随机投射300个点，并统计落在小圆中不含边界）的点数，经历大量试验，发现随机点落在小圆中的点数稳定在100粒左右，则可估计小圆的面积为．

查看试题解析

三、解答题

14. 在一个不透明的盒子中装有n个小球，它们只有颜色上的区别，其中有2个红球，每次摸球前先将盒中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复试验后发现，摸到红球的频率稳定于0.2，请你估计n的值．

查看试题解析
15. 某工厂生产的一批零件，出现次品的概率为5%，若生产这种零件10000个，大约出现次品多少个？

查看试题解析
16. 篮球运动员甲的三分球命中率是70%，乙的三分球命中率是50%．本场比赛中甲投三分球4次，命中1次；乙投三分球4次，全部命中．全场比赛结束前，甲、乙两人所在球队还落后对方球队2分，但还有一次进攻的机会．如果你是教练，那么最后一个三分球由谁来投？说说你的理由．

查看试题解析
17. 下表是某厂质检部门对该厂生产的一批排球质量检测的情况．
抽取的排球数描取格品数
$500$
$1000$
$1500$
$2000$
$3000$
合格品数
$471$
$946$
$1425$
$b$
$2853$
合格品频率
$a$
$0.946$
$0.950$
$0.949$
$0.951$

(1)、求出表中 $a =$ ， $b =$ ．

(2)、从这批排球中任意抽取一个，是合格品的概率约是 $. ($ 精确到 $0.01)$

(3)、如果生产 $25000$ 个排球，那么估计该厂生产的排球合格的有多少个？

查看试题解析

18. 某水果公司新进了

10000

千克柑橘，销售人员首先从所有的柑橘中随机地抽取若干柑橘，进行了“柑橘损坏率”统计，并把获得的数据记录在下表中：

柑橘总质量（ $n$ /千克）	损坏柑橘质量（ $m$ /千克）	柑橘损坏的频率（ $\frac{m}{n}$ ）
$50$	$5.50$	$0.110$
$100$	$10.50$	$0.105$
$150$	$15.15$	$0.101$
$200$	$19.42$	$0.097$
$250$	$24.35$	$0.097$
$300$	$30.93$	$a$
$350$	$35.32$	$0.101$
$400$	$39.24$	$b$
$450$	$44.57$	$0.099$
$500$	$51.54$	$c$

(1)、写出

a =

▲

b =

▲

c =

▲ （精确到

0.001

）.

(2)、估计这批柑橘的损坏概率为 ▲ （精确到

0.1

）.

(3)、该水果公司以

2

元每千克的成本进的这批柑橘，公司希望这批柑橘能够获得利润

5000

元，那么在出售柑橘（已去掉损坏的柑橘）时，求出每千克大约定价为多少元时比较合适（精确到

0.1

）.

查看试题解析

19. 在一个不透明的口袋里装有若干个相同的红球，为了估计袋中红球的数量，七年级（2）班学生在数学实验室分组做摸球试验：每组先将10个与红球大小、形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色，再把它放回袋中，不断重复，下面是全班各小组的汇总数据统计表：
摸球次数 $s$
150
300
600
900
1200
1500
摸到白球的频数 $n$
63
123
247
365
484
603
摸到白球的频率 $\frac{n}{s}$
$0.420$
$0.410$
$0.412$
$0.406$
$0.403$
$a$

(1)、表中的 $a =$ ；

(2)、请估计当摸球次数s很大时，摸到白球的频率将会接近（精确到 $0.1$ ）

(3)、试估算摸到红球的概率是（精确到 $0.1$ ）

(4)、试估算这个不透明的口袋中红球的个数．

查看试题解析
20.
某商场“五一”期间为进行有奖销售活动，设立了一个可以自由转动的转盘．商场规定：顾客购物100元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品．下表是此次活动中的一组统计数据：
转动转盘的次数n
100
200
400
500
800
1000
落在“可乐”区域的次数m
60
122
240
298

604
落在“可乐”区域的频率 $\frac{m}{n}$
0.6
0.61
0.6

0.59
0.604
（1）完成上述表格；（结果全部精确到0.1）
（2）请估计当n很大时，频率将会接近　？，假如你去转动该转盘一次，你获得“可乐”的概率约是　？　；（结果全部精确到0.1）
（3）转盘中，表示“洗衣粉”区域的扇形的圆心角约是多少度？

查看试题解析

累计抛掷次数	50	100	200	300	500	1000	2000	3000	5000
盖面朝上次数	28	54	106	158	264	527	1056	1587	2650
盖面朝上频率	0.5600	0.5400	0.5300	0.5267	0.5280	0.5270	0.5280	0.5290	0.530

抽取的排球数描取格品数	$500$	$1000$	$1500$	$2000$	$3000$
合格品数	$471$	$946$	$1425$	$b$	$2853$
合格品频率	$a$	$0.946$	$0.950$	$0.949$	$0.951$

摸球次数 $s$	150	300	600	900	1200	1500
摸到白球的频数 $n$	63	123	247	365	484	603
摸到白球的频率 $\frac{n}{s}$	$0.420$	$0.410$	$0.412$	$0.406$	$0.403$	$a$

转动转盘的次数n	100	200	400	500	800	1000
落在“可乐”区域的次数m	60	122	240	298		604
落在“可乐”区域的频率 $\frac{m}{n}$	0.6	0.61	0.6		0.59	0.604

【基础版】北师大版数学九年级上册3.2用频率估计概率 同步练习

一、选择题

二、填空题

三、解答题

【基础版】北师大版数学九年级上册3.2用频率估计概率同步练习