【培优版】北师大版数学八年级上册第四章一次函数章节测试卷

试卷更新日期：2024-09-24 类型：单元试卷

进入出卷网下载

一、选择题(本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

1. 如果一次函数当自变量 $x$ 的取值范围是 $- 1 < x < 3$ 时，函数值y的取值范围是 $- 2 < y < 6$ ，那么此函数的解析式是（）

A、 $y = 2 x$ B、 $y = - 2 x + 4$ C、 $y = 2 x$ 或 $y = - 2 x + 4$ D、 $y = - 2 x$ 或 $y = 2 x - 4$

查看试题解析
2. 如图，在平面直角坐标系中，一次函数 $y = x + 4$ 的图象与x轴交于点A ，与y轴交于点B ，点P在线段 $A B$ 上， $P C ⊥ x$ 轴于点C ，则 $△ P C 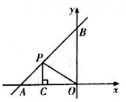O$ 周长的最小值为（）

A、 $2 \sqrt{2}$ B、 $4 + 2 \sqrt{2}$ C、4 D、 $4 + 4 \sqrt{2}$

查看试题解析
3. 如图，四边形ABCD的顶点坐标分别为4（-4，0），B（-2，-1），C（3，0），D（0，3），当过点B的直线l将四边形ABCD分成面积相等的两部分时，直线I所表示的函数表达式为（）

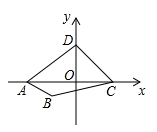A、y= $\frac{11}{10} x + \frac{6}{5}$ B、y= $\frac{2}{3} x + \frac{1}{3}$ C、y=x+1 D、y= $\frac{5}{4} x + \frac{3}{2}$

查看试题解析
4. 如图，直线y=-x+4分别与x轴，y轴交于A，B两点．从点P(2，0)射出的光线经直线AB反射后又经直线OB反射回到P点，则光线第一次的反射点Q的坐标是（）

A、(2，2) B、(2.5，1.5) C、(3，1) D、(1.5，2.5)

查看试题解析
5. 甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．则下列结论：
①A，B两城相距 $300$ 千米；
②乙车比甲车晚出发 $1$ 小时，却早到 $1$ 小时；
③乙车出发后 $1.5$ 小时追上甲车；
④当甲、乙两车相距 $50$ 千米时， $t = \frac{5}{4}$ 或 $\frac{15}{4}$
其中正确的结论有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
6. 若点 $(x_{1}, y_{1})$ 、 $(x_{2}, y_{2})$ 是一次函数 $y = - a x - x + 2$ 图象上不同的两点，记 $m = (x_{1} - x_{2}) (y_{1} - y_{2})$ ，当 $m < 0$ 时，a的取值范围是（）

A、 $a < 0$ B、 $a > 0$ C、 $a < - 1$ D、 $a > - 1$

查看试题解析
7. 甲、乙两人登山，登山过程中，甲、乙两人距地面的高度y（米）与登山时间x（分钟）之间的函数图象如图所示．乙提速后，乙的登山速度是甲登山速度的3倍，并先到达山顶．根据图象所提供的信息，下列说法正确的有（）
①甲登山的速度是每分钟10米；②乙在A地时距地面的高度b为30米；③乙登山 $5.5$ 分钟时追上甲；④登山时间为4分钟、9分钟、13分钟时，甲、乙两人距地面的高度差为50米．

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 在同一直角坐标系中，一次函数 $y = m x + n$ （ $m$ 和 $n$ 是常数）与 $y = n x + m$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题共5小题, 每小题3分, 共15分)

9. 如图，直线AB的解析式为y＝-x+b ，分别与x轴，y轴交于A ， B两点，点A的坐标为（4，0），过点B的直线交x轴负半轴于点C ，且OB：OC＝4：1．若在x轴上方存在点D ，使以A ， B ， D为顶点的三角形与△ABC全等，则点D的坐标为．

查看试题解析
10. 如图，直线 $y = 2 x + 4$ 与 $x$ 轴、 $y$ 轴交于点 $A$ 、 $B$ ， $M$ 、 $N$ 分别是 $A B$ 、 $O A$ 的中点，点 $P$ 是 $y$ 轴上一个动点，当 $P M + P N$ 的值最小时，点 $P$ 的坐标为．

查看试题解析
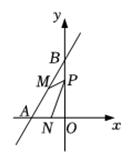11. 如图，平面直角坐标系中，A（4，4），B为y轴正半轴上一点，连接AB，在第一象限作AC＝AB，∠BAC＝90°，过点C作直线CD⊥x轴于D，直线CD与直线y＝x交于点E，且ED＝5EC，则直线BC解析式为．

查看试题解析
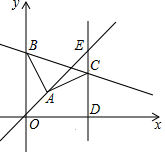12. 如图放置的△OAB₁ ， △B₁A₁B₂ ， OB₂A₂B₃都是边长为2的等边三角形，边0A在y轴上，点B₁ ， B₂ ， B₃ ， ……都在直线y＝ $\frac{\sqrt{3}}{3}$ x上，则点A₂₀₂₂的坐标是

查看试题解析
13. 已知A、B、C三地顺次在同一直线上，A、C两地相距1400千米，甲乙两车均从A地出发，向B地方向匀速前进，甲车出发5小时后，乙车出发，经过一段时间后两车在B地相遇，甲车到达B地后便在B地卸货，卸完货后从B地按原车速的 $\frac{4}{3}$ 返回A地，而乙车到B地后立刻继续以原速前往C地，到达C地后按原车速的 $\frac{5}{4}$ 原路返回A地，结果甲乙两车同时返回A地，若两车间的距离y（千米）与甲车出发时间x（小时）之间的关系如图所示，则甲车在B地卸货用了小时．

查看试题解析

三、解答题（共7题，共61分）

14. 如图所示，在平面直角坐标系xOy中，直线y=- $\frac{4}{3}$ x+4与x轴、y轴分别交于点A、点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处.

(1)、求AB的长.

(2)、求点C和点D的坐标.

(3)、y轴上是否存在一点P，使得S_△_PAB= $\frac{1}{2}$ S_△_OCD?若存在，求出点P的坐标；若不存在，请说明理由.

查看试题解析
15. 在平面直角坐标系中，直线 $y = \frac{1}{2} x + b$ 与 $x$ 轴交于点A ，与 $y$ 轴交于点 $B$ ，点 $P$ 坐标为 $(3 ， 0)$ ，过点 $P$ 作 $P C ⊥ x$ 轴，且 $△ A B C$ 为等腰直角三角形．

(1)、如图，当 $∠ B A C = 90 °$ ， $A B = A C$ 时，求证： $△ A B O ≌ △ C A P$ ；

(2)、当 $A B$ 为直角边时，请给出相应图形分别求出所有可能的 $b$ 值，并直接写出点 $C$ 的坐标．

查看试题解析
16. 甲、乙两地之间有一条笔直的公路，小明从甲地出发步行前往乙地，同时小亮从乙地出发骑自行车前往甲地，小亮到达甲地没有停留，按原路原速返回，追上小明后两人一起步行到乙地．如图，线段OA表示小明与甲地的距离 $y_{1}$ （米）与行走的时间x（分钟）之间的函数关系：折线BCDA表示小亮与甲地的距离 $y_{2}$ （米）与行走的时间x（分钟）之间的函数关系，请根据图象解答下列问题：

(1)、小明步行的速度是米/分钟，小亮骑自行车的速度是米/分钟；

(2)、线段OA与BC相交于点E ，求点E坐标；

(3)、请直接写出小亮从乙地出发到追上小明的过程中，与小明相距100米时x的值．

查看试题解析
17. 已知一次函数 $y = k x + b$ ．当 $x = - 3$ 时， $y = - 8$ ；当 $x = 0$ 时， $y = - 4$ ．

(1)、求该一次函数的表达式；

(2)、求该函数的图象与坐标轴围成的图形的面积．

查看试题解析
18. 如图，在平面直角坐标系中，一次函数 $y = - \frac{1}{2} x + 3$ 的图象分别与 $x$ 轴、 $y$ 轴交于点 $A$ ， $B$ ，点 $C$ 是线段 $O A$ 上的一个动点（不与点 $O$ ，点 $A$ 重合），过点 $C$ 作 $x$ 轴的垂线交直线 $A B$ 于点 $D$ ，在射线 $C D$ 上取点 $E$ ，使 $C E = 2 O C$ .设点 $C$ 的横坐标为 $m$ .

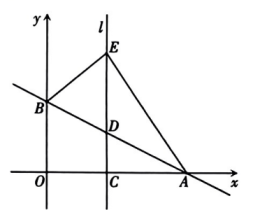(1)、求 $A$ ， $B$ 两点的坐标；

(2)、若点 $E$ 落在直线 $A B$ 上，求 $m$ 的值；

(3)、请从A，B两题中任选一题作答.我选择题.
$A$ .若线段 $D E$ 的长等于 $O B$ 的一半时，求 $m$ 的值.
$B$ .若 $△ A B E$ 的面积等于 $△ A O B$ 面积的一半，求 $m$ 的值.

查看试题解析
19. 如图①，平面直角坐标系中，O为原点，点A坐标为（﹣4，0），AB∥y轴，点C在y轴上，一次函数y= $\frac{1}{4}$ x+3的图象经过点B、C．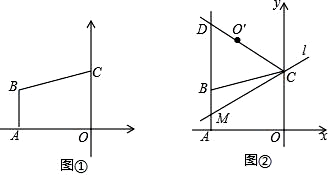

(1)、点C的坐标为，点B的坐标为；

(2)、如图②，直线l经过点C，且与直线AB交于点M，O'与O关于直线l对称，连接CO'并延长，交射线AB于点D．
①求证：△CMD是等腰三角形；
②当CD=5时，求直线l的函数表达式．

查看试题解析
20. 如图所示，把矩形纸片OABC放入直角坐标系xOy中，使OA、OC分别落在x、y轴的正半轴上，连接AC，且AC=4 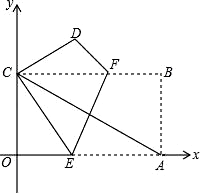$\sqrt{5}$ ， $\frac{O C}{O A} = \frac{1}{2}$

(1)、求AC所在直线的解析式；

(2)、将纸片OABC折叠，使点A与点C重合（折痕为EF），求折叠后纸片重叠部分的面积．

(3)、求EF所在的直线的函数解析式．

查看试题解析

【培优版】北师大版数学八年级上册第四章 一次函数 章节测试卷

一、选择题(本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

二、填空题（本大题共5小题, 每小题3分, 共15分)

三、解答题（共7题，共61分）

【培优版】北师大版数学八年级上册第四章一次函数章节测试卷