【基础版】北师大版数学八年级上册第四章 一次函数 章节测试卷
试卷更新日期:2024-09-23 类型:单元试卷
一、选择题(本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的)
-
1. 下列图象中,y不是x的函数图象的是( )A、
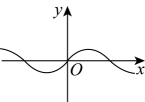 B、
B、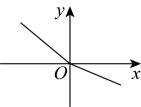 C、
C、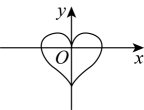 D、
D、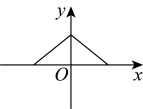 2. 下列4个函数关系:y=2x+1,y= ,s=60t,y=100﹣25x,其中是一次函数的共有( )A、1个 B、2个 C、3个 D、4个3. 函数y=+x-2的自变量x的取值范围是( )A、x≥2 B、x>2 C、x≠2 D、x≤24. 下列各点中,在直线上的是A、 B、 C、 D、5. 一次函数的图象是由的图象平移得到的,则移动方法为( )A、向右平移个单位 B、向左平移个单位 C、向上平移个单位 D、向下平移个单位6. 已知直线y1=x, , y3=-x+5,若无论x取何值,y总是取y1 , y2 , y3中的最小值,则y的最大值是( )
2. 下列4个函数关系:y=2x+1,y= ,s=60t,y=100﹣25x,其中是一次函数的共有( )A、1个 B、2个 C、3个 D、4个3. 函数y=+x-2的自变量x的取值范围是( )A、x≥2 B、x>2 C、x≠2 D、x≤24. 下列各点中,在直线上的是A、 B、 C、 D、5. 一次函数的图象是由的图象平移得到的,则移动方法为( )A、向右平移个单位 B、向左平移个单位 C、向上平移个单位 D、向下平移个单位6. 已知直线y1=x, , y3=-x+5,若无论x取何值,y总是取y1 , y2 , y3中的最小值,则y的最大值是( ) A、 B、3 C、 D、27. 在一次800米的长跑比赛中,甲、乙两人所跑的路程 (米)与各自所用时间 (秒)之间的函数图象分别为线段 和折线 ,则下列说法不正确的是( )
A、 B、3 C、 D、27. 在一次800米的长跑比赛中,甲、乙两人所跑的路程 (米)与各自所用时间 (秒)之间的函数图象分别为线段 和折线 ,则下列说法不正确的是( ) A、甲的速度保持不变 B、乙的平均速度比甲的平均速度大 C、在起跑后第180秒时,两人不相遇 D、在起跑后第50秒时,乙在甲的前面8. 关于一次函数 , 下列结论正确的是( )A、图象不经过第二象限 B、图象与x轴的交点是(0,2) C、将一次函数的图象向上平移1个单位长度后,所得图象的函数表达式为 D、点(x1 , y1)和(x2 , y2)在一次函数的图象上,若x1<x2 , 则y1>y2
A、甲的速度保持不变 B、乙的平均速度比甲的平均速度大 C、在起跑后第180秒时,两人不相遇 D、在起跑后第50秒时,乙在甲的前面8. 关于一次函数 , 下列结论正确的是( )A、图象不经过第二象限 B、图象与x轴的交点是(0,2) C、将一次函数的图象向上平移1个单位长度后,所得图象的函数表达式为 D、点(x1 , y1)和(x2 , y2)在一次函数的图象上,若x1<x2 , 则y1>y2二、填空题(本大题共5小题, 每小题3分, 共15分)
-
9. 若点 , 都在一次函数的图象上,则 . (填“”或“”)10. 若函数y=(m+2)x|m|﹣1﹣5是一次函数,则m的值为.11. 将正比例函数y=﹣3x的图象向上平移5个单位,得到函数的图象.12. 某市出租车白天的收费起步价为7元,即路程不超过3千米时收费7元,超过部分每千米收费 元,如果乘客白天乘坐出租车的路程为 千米,乘车费为 元,那么 与 之间的关系为.13. 某公司准备与汽车租赁公司签订租车合同,以每月用车路程x(千米)计算,甲汽车租赁公司每月收取的租赁费为y1元,乙汽车租赁公司每月收取的租赁费为y2元,y1 , y2与x之间的函数关系如图所示.当月用车路程为2300千米时,选汽车租赁公司比较合算.

三、解答题(共7题,共61分)
-
14. 若是y关于x的正比例函数,求该正比例函数的解析式.15. 已知弹簧的长度y(厘米)在一定的限度内是所挂物质量x(千克)的一次函数.现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7. 2厘米,求这个一次函数的关系式.16. 据科学研究,10至50岁的人每天所需睡眠时间H(时)可用公式H=(N是人的年龄)来计算,写出其中的变量和常量.用这个公式算一算,你每天需要多少小时的睡眠时间?17. 一水池的容积是 , 现蓄水 , 用水管以的速度向水池注水,直到注满为止.
(1)写出蓄水量与注水时间之间的关系式
(2)当时,V的值是多少?
(3)要注满水池容积80%的水,需要多少小时?
18. 游泳池应定期换水.某游泳池在一次换水前存水900立方米,换水时打开排水孔,以每小时300立方米的速度将水放出.设放水时间为小时,游泳池内存水量为立方米.(1)、求关于的函数表达式和自变量的取值范围;(2)、放水多少小时后,游泳池内存水量小于300立方米?19. 近年来,宣城市不断践行德智体美劳“五育并举”目标,努力将劳动教育落到实处,某校八年级策划举行劳动技能比赛,计划购买A , B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元.根据比赛设奖情况,需购买笔记本共30本.(1)、设买A种笔记本n本,买两种笔记本的总费用为w元,求w关于n的函数表达式.(2)、在(1)的条件下,若购买A种笔记本的数量不多于B种笔记本数量的 , 但又不少于B种笔记本数量的 , 则购买这两种笔记本各多少时费用最少?最少的费用是多少元?20. 甲、乙两地相距千米,一辆货车和一辆轿车先后从甲地出发开往乙地.如图,线段表示货车离甲地距离千米与时间小时之间的函数关系;折线表示轿车离甲地距离千米与小时之间的函数关系.请根据图象解答下列问题: (1)、求线段对应的函数解析式.(2)、货车从甲地出发后多长时间被轿车追上?此时离甲地的距离是多少千米?(3)、轿车到达乙地后,货车距乙地多少千米.
(1)、求线段对应的函数解析式.(2)、货车从甲地出发后多长时间被轿车追上?此时离甲地的距离是多少千米?(3)、轿车到达乙地后,货车距乙地多少千米.