广东省惠州市惠阳高级中学2024-2025学年九年级上学期开学考试数学试题
试卷更新日期:2024-09-23 类型:开学考试
一、选择题(共10小题,每小题3分,共30分)
-
1. 以下列各组数为边长,能构成直角三角形的是( )A、 , , 2 B、6,8,10 C、4,5,6 D、5,10,122. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、3. 在▱ABCD中,如果∠A+∠C=140°,那么∠C等于( )A、20° B、40° C、60° D、70°4. 下列各图象中,( )表示y是x的一次函数.A、
 B、
B、 C、
C、 D、
D、 5. 用配方法解方程 ,下列变形正确的是( )A、 B、 C、 D、6. 为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:cm)的平均数与方差为: = =13, = =15:s甲2=s丁2=3.6,s乙2=s丙2=6.3.则麦苗又高又整齐的是( )
5. 用配方法解方程 ,下列变形正确的是( )A、 B、 C、 D、6. 为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:cm)的平均数与方差为: = =13, = =15:s甲2=s丁2=3.6,s乙2=s丙2=6.3.则麦苗又高又整齐的是( )
A、甲 B、乙 C、丙 D、丁7. 如图,在中,点在上, , 于点 , 是的中点,连接 , 若 , , 则的长为( ) A、6 B、3 C、1.5 D、18. 如图, 为等腰三角形,如果把它沿底边 翻折后,得到 ,那么四边形ABDC为( )
A、6 B、3 C、1.5 D、18. 如图, 为等腰三角形,如果把它沿底边 翻折后,得到 ,那么四边形ABDC为( )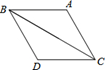 A、一般平行四边形 B、正方形 C、矩形 D、菱形9. 如图,直线 与 相交于点 ,点 的横坐标为 ,则关于 的不等式 的解集在数轴上表示正确的是( )
A、一般平行四边形 B、正方形 C、矩形 D、菱形9. 如图,直线 与 相交于点 ,点 的横坐标为 ,则关于 的不等式 的解集在数轴上表示正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在四边形中, , , 于点 , 如果四边形的面积为8,那么的长为( )
10. 如图,在四边形中, , , 于点 , 如果四边形的面积为8,那么的长为( ) A、2 B、4 C、 D、
A、2 B、4 C、 D、二、填空题(共5小题,每小题3分,共15分)
-
11. 要使式子 有意义,则a的取值范围为 .12. 已知a,b是两个连续的整数,若 , 则.13. 菱形的两条对角线长分别是方程 的两实根,则菱形的面积为 .14. 如图,在矩形中,是上一点, , , 则的度数是 .
 15. 在平面直角坐标系中,正方形、、 , …,按在图所示的方式放置.点、、 , …和、、 , …分别在直线和轴上.已知 , , 则点的坐标是;点的坐标是 .
15. 在平面直角坐标系中,正方形、、 , …,按在图所示的方式放置.点、、 , …和、、 , …分别在直线和轴上.已知 , , 则点的坐标是;点的坐标是 .
三、解答题(共3小题,每小题8分,共24分)
-
16. 解答(1)、计算;(2)、解方程 .17. 已知的周长为 , 其中 , .(1)、求的长度;(2)、判断是否为直角三角形,并说明理由.18. 如图,在平行四边形ABCD中,AE平分∠BAC , CF平分∠ACD .
 (1)、求证:△ABE≌△CDF;(2)、若AB=AC , 请判断四边形AECF的形状,并说明理由.
(1)、求证:△ABE≌△CDF;(2)、若AB=AC , 请判断四边形AECF的形状,并说明理由.四、解答题(共3小题,每小题9分,共27分)
-
19. 某学校七八两个年级各有学生500人.为了普及冬奥如识.学校在七八年级举行了一次冬奥知识竞赛,为了解这两个年级学生的冬奥知识竞赛成绩(百分制),分别从两个年级各随机抽取了20名学生的成绩进行整理、描述和分析,下面给出了部分信息.
a、七八年级的样本成绩分布如下:
七
0
0
0
0
4
3
7
4
2
0
八
1
1
0
0
0
4
6
5
2
1
(说明:成绩在50分以下为不合格.在分为合格,70分及以上为优秀)
b、七年级成绩在一组的是:61,62,63,65,66,68,69
c、七八年级成绩的平均数、中位数、优秀率、合格率如下:
年级
平均数
中位数
优秀率
合格率
七
64.7
八
63.3
67
根据以上信息,回答下列问题:
(1)、上述表中 , ;(2)、小军的成绩在此次抽样之中,与他所在的年级的抽样相比,小军的成绩高于平均数,却排在了后十名,则小军是年级的学生;(选填“七”或“八”)(3)、根据样本数据,请估计参加这次竞赛活动优秀学生人数;(4)、根据样本数据,你认为哪个年级的竞赛成绩更好,请说明理由.20. 配方(1)、若 , 则 , ;(2)、如图,在中, , , , 动点从点开始沿边向点以的速度移动,动点从点开始沿边以的速度移动.如果、两点分别从、两点同时出发,同时停止运动.设动点运动时间为 , 当为何值时,的面积最大?求该最大值. 21. 某大学生创业,购进A、B共300件,进货时发现:8件A商品和4件B商品进货需要72元;4件A商品和3件B商品进货需要38元,设B的件数80≤x≤200 , A , B的总售价分别为函数z1 , z2.
21. 某大学生创业,购进A、B共300件,进货时发现:8件A商品和4件B商品进货需要72元;4件A商品和3件B商品进货需要38元,设B的件数80≤x≤200 , A , B的总售价分别为函数z1 , z2.z1与销售件数之间是一次函数的关系,如下表:
销售件数x
0
1
2
3
4
总售价
0
10
20
30
40
z2与x的函数关系如图所示:
 (1)、直接写出z1 , z2与x的函数关系;(2)、设销售A , B两种商品所获利总利润为y元,求y与x之间的函数解析式;(3)、大学生引进的300件A , B商品全部售完,共获利350元,他计划每件A , B商品捐给学校基金分别捐2m元,m元,捐款数恰好为总成本的10%,求m的值.
(1)、直接写出z1 , z2与x的函数关系;(2)、设销售A , B两种商品所获利总利润为y元,求y与x之间的函数解析式;(3)、大学生引进的300件A , B商品全部售完,共获利350元,他计划每件A , B商品捐给学校基金分别捐2m元,m元,捐款数恰好为总成本的10%,求m的值.五、解答题(共2小题,每小题12分,共24分)
-
22. 如图,在平面直角坐标系中,函数的图象分别交轴,轴于A , 两点,过点A的直线交轴正半轴于点 , 且点为线段的中点.
 (1)、求直线的函数解析式;(2)、试在直线上找一点 , 使得 , 请求出点的坐标;(3)、若点为坐标平面内任意一点,在坐标平面内是否存在这样的点 , 使以 , , , 为顶点的四边形是平行四边形?若存在,请直接写出所有点的坐标;若不存在,请说明理由.23. 综合探究:
(1)、求直线的函数解析式;(2)、试在直线上找一点 , 使得 , 请求出点的坐标;(3)、若点为坐标平面内任意一点,在坐标平面内是否存在这样的点 , 使以 , , , 为顶点的四边形是平行四边形?若存在,请直接写出所有点的坐标;若不存在,请说明理由.23. 综合探究:“在中,、、三边的长分别为、、 , 求这个三角形的面积”.
小明同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点(即三个顶点都在小正方形的顶点处),如图1所示,这样不需求的高,而借用网格就能计算出它的面积.我们把上述求面积的方法叫做构图法.
 (1)、直接写出图1中的面积是______;(2)、若的边长分别为、、( , , 且),试运用构图法在图2中画出相应的 , 并求出的面积.(3)、拓展应用:求代数式:的最小值.
(1)、直接写出图1中的面积是______;(2)、若的边长分别为、、( , , 且),试运用构图法在图2中画出相应的 , 并求出的面积.(3)、拓展应用:求代数式:的最小值.