四川省自贡市自流井区解放路中学2024-2025学年九年级上学期数学开学考试试卷

试卷更新日期：2024-09-23 类型：开学考试

进入出卷网下载

一、选择题（共12小题，满分48分，每小题4分）

1. 能够使二次根式 $\sqrt{2 x - 3}$ 有意义的实数x的取值范围是（　　）

A、 $x > \frac{3}{2}$
B、 $x ⩾ \frac{3}{2}$
C、 $x < \frac{3}{2}$
D、 $x ⩽ \frac{2}{3}$

查看试题解析
2. 以下列各组数为边长构造三角形，不是直角三角形的是（　　）

A、2，2，3 B、 $1, \sqrt{3}, 2$ C、5，12，13 D、3，4，5

查看试题解析
3. 下列各式中，最简二次根式是（　　）

A、 $\sqrt{8}$
B、 $\sqrt{m^{5} n^{2}}$
C、 $\sqrt{6}$
D、 $\sqrt{\frac{1}{3}}$

查看试题解析
4. 一组数据：10、5、15、5、20，则这组数据的平均数和中位数分别是（　　）

A、10，10 B、11，10 C、11，12.5 D、10，12.5

查看试题解析
5. 下面给出的条件中，能判定四边形ABCD是平行四边形的是（　　）

A、AB＝AD ， CB＝CD B、AD∥BC ， ∠A＝∠C C、AD∥BC ， ∠A＝∠B D、AB＝AD ， ∠B＝∠D

查看试题解析
6. 一次函数y＝kx+b（k≠0）的图象情况如图所示，则关于k、b的分析正确的是（　　）

A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜0

查看试题解析
7. 如图，甲乙两艘轮船从某港口O同时出发，各自沿一固定方向航行，其中甲航行方向为北偏西60°，乙航行方向为北偏东30°，甲每小时航行12海里，乙每小时航行16海里，他们离开港口两小时后分别位于点A、B处，则此时两船相距（　　）海里．

A、36 B、40 C、48 D、50

查看试题解析
8. 如图，直线y＝﹣x+b和y＝kx﹣3交于点P ，根据图象可知kx﹣3＜﹣x+b的解集为（　　）

A、x＞1 B、x＜1 C、0＜x＜1 D、﹣2＜x＜1

查看试题解析
9. 如图，正方形ABCD的边长为18，将正方形折叠，使顶点D落在BC边上的点E处，折痕为GH ．若BE：EC＝2：1，则线段CH的长是（　　）

A、6 B、8 C、10 D、12

查看试题解析
10. 如图，正方形ABCD的边长为 $2 \sqrt{2}$ ， O是对角线BD上一动点（点O与端点B ， D不重合），OM⊥AD于点M ， ON⊥AB于点N ，连接MN ，则MN长的最小值为（　　）

A、1 B、2 C、 $\sqrt{2}$ D、 $2 \sqrt{2}$

查看试题解析
11. 如图，函数y＝﹣x+2图象与x轴、y轴分别交于A、B两点，C（1，0），点P为直线AB上动点，连接OP、PC ，则△OPC的周长最小值为（　　）

A、3 B、4 C、 $\sqrt{5} + 1$ D、 $2 \sqrt{2} + 1$

查看试题解析
12. 如图，P为等边三角形ABC内的一点，且P到三个顶点A ， B ， C的距离分别为3，4，5，则△ABC的面积为（　　）

A、 $9 + \frac{25 \sqrt{3}}{4}$
B、 $9 + \frac{25 \sqrt{3}}{2}$
C、 $18 + 25 \sqrt{3}$
D、 $18 + \frac{25 \sqrt{3}}{2}$

查看试题解析

二、填空题（共6小题，满分24分，每小题4分）

13. 在平面直角坐标系中，直线y＝2x﹣1向上平移2个单位，所得的直线的解析式是．

查看试题解析
14. 在学校团体操比赛中，甲、乙两个班的同学身高的平均数相同，方差分别是S_甲²＝1.8，S_乙²＝1.3，那么身高整齐的是班．

查看试题解析
15. 有一棵9米高的大树距离地面4米处折断（未完全断开），则大树顶端触地点距大树的距离为米．

查看试题解析
16. 已知 $a = \sqrt{2} + 1, b = \sqrt{2} - 1$ ，则 $\sqrt{a b + 7}$ ＝．

查看试题解析
17. 如图，在四边形ABCD中，E、F、G、H分别是AB、BD、CD、AC的中点，要使四边形EFGH是菱形，四边形ABCD还应满足的一个条件是．

查看试题解析
18. 如图，直线y＝3x+6交坐标轴于A、B两点，C为AB中点，点D为AO上一动点，点E在x轴正半轴上，且满足OE＝OD+OB ，则 $\sqrt{2} C D + D E$ 的最小值为．

查看试题解析

三、解答题（共8小题，满分78分）

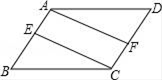
19. 计算： $\sqrt{48} + \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{24} + \sqrt{2}$ ．

查看试题解析
20. 如图，在平行四边形ABCD中，AE=CF，求证：AF=CE．

查看试题解析
21. 如图，在长方形ABCD中，将△ABC沿AC对折至△AEC位置，CE与AD交于点F．

(1)、试说明：AF＝FC；

(2)、如果AB＝3，BC＝4，求AF的长．

查看试题解析
22. 如图，一次函数y₁＝2x﹣2的图象与y轴交于点A ，一次函数y₂的图象与y轴交于点B（0，6），点C为两函数图象的交点，且点C的横坐标为2．

(1)、求一次函数y₂的函数解析式；

(2)、求△ABC的面积；

查看试题解析
23. 某地为了解“阳光体育”运动推进情况，就“中小学每天在校体育活动时间”的问题随机调查了330名中小学生：根据调查结果绘制成的统计图的一部分如图（其中分组情况见下表）：
组别

A
$t < 0.5$
B
$0.5 \leq t < 1$
C
$1 \leq t < 1.5$
D
$t \geq 1.5$
请根据上述信息解答下列问题：

(1)、补全条形统计图；

(2)、本次调查数据（指体育活动时间）的中位数落在______组内；

(3)、若某地约有6600名中小学生，请你估计其中没有达到国家规定体育活动时间（不低于1小时）的人数约有多少？

查看试题解析
24. 在二次根式中，有些根式相乘，其结果是实数．
如 $(2 + \sqrt{3}) (2 - \sqrt{3}) = 1$ ， $(\sqrt{5} + \sqrt{2}) (\sqrt{5} - \sqrt{2}) = 3$ ，它们的积不含根号，我们说这两个二次根式互为有理化因式，其中一个是另一个的有理化因式．于是，二次根式除法可以这样解：如 $\frac{1}{\sqrt{3}} = \frac{1 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{\sqrt{3}}{3}$ ， $\frac{2 + \sqrt{3}}{2 - \sqrt{3}} = \frac{(2 + \sqrt{3}) (2 + \sqrt{3})}{(2 - \sqrt{3}) (2 + \sqrt{3})} = 7 + 4 \sqrt{3}$ ，像这样，通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去，叫做分母有理化．

(1)、解决问题： $3 - \sqrt{5}$ 的有理化因式是_____， $\frac{2}{3 \sqrt{2}}$ 分母有理化，得______；

(2)、计算： $\frac{1}{2 - \sqrt{3}} + \sqrt{12} - 9 \sqrt{\frac{1}{3}}$ ；

(3)、化简： $\frac{2}{\sqrt{3} + 1} + \frac{2}{\sqrt{5} + \sqrt{3}} + \frac{2}{\sqrt{7} + \sqrt{5}} + \dots \dots + \frac{2}{\sqrt{2023} + \sqrt{2021}} - \sqrt{2023}$ ．

查看试题解析
25. 如图，四边形 $A B C D$ 中， $∠ D A B = 45 °$ ， $A B = 8$ ， $A D = 3 \sqrt{2}$ ， $E$ 为 $A B$ 中点，且 $C D ⊥ D E$ ，连接 $C E$ ．

(1)、求 $D E$ 的长度；

(2)、若 $∠ B E C = ∠ A D E$ ，求 $B C$ 的长度．

查看试题解析
26. 如图，一次函数y₁＝﹣3x+b的图象分别交y轴，x轴于点A ， B ，一次函数y₂＝mx﹣6的图象分别交y轴，x轴于点C ， D ，两个一次函数的图象相交于点E（2，﹣3）．

(1)、求y₁ ， y₂的解析式；

(2)、若直线y₂＝mx﹣6上存在一点P ，使S_△_ACP＝4S_△_BDE ，求符合条件的点P的坐标；

(3)、若点M为平面直角坐标系内任意一点，是否存在这样的点M ，使以A ， D ， E ， M为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．

查看试题解析

组别
A	$t < 0.5$
B	$0.5 \leq t < 1$
C	$1 \leq t < 1.5$
D	$t \geq 1.5$