【培优版】北师大版数学八年级上册4.4一次函数的应用 同步练习
试卷更新日期:2024-09-23 类型:同步测试
一、选择题
-
1. 如图,直线与x轴,y轴分别交于点A和点B,点C在线段上,且点C坐标为 , 点D为线段的中点,点P为上一动点,当的周长最小时,点P的坐标为( )
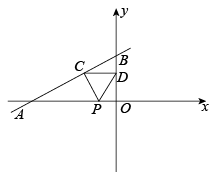 A、 B、 C、 D、2. 将一次函数与的图象画在同一平面直角坐标系中,则下列图象中正确的是( )A、
A、 B、 C、 D、2. 将一次函数与的图象画在同一平面直角坐标系中,则下列图象中正确的是( )A、 B、
B、 C、
C、 D、
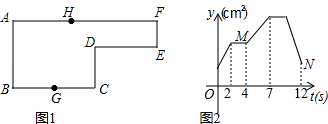
D、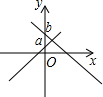 3. 如图1,点G为BC边的中点,点H在AF上,动点P以每秒2cm的速度沿图1的边运动,运动路径为G→C→D→E→F→H,相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图象如图2,若AB=6cm,则下列结论正确的个数有( )
3. 如图1,点G为BC边的中点,点H在AF上,动点P以每秒2cm的速度沿图1的边运动,运动路径为G→C→D→E→F→H,相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图象如图2,若AB=6cm,则下列结论正确的个数有( )①图1中BC长4cm;
②图1中DE的长是6cm;
③图2中点M表示4秒时的y值为24cm2;
④图2中的点N表示12秒时y值为15cm2 .
 A、4个 B、3个 C、2个 D、1个4.
A、4个 B、3个 C、2个 D、1个4.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(甲车休息前后的速度相同),甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示.根据图象的信息有如下四个说法:
①甲车行驶40千米开始休息
②乙车行驶3.5小时与甲车相遇
③甲车比乙车晚2.5小时到到B地
④两车相距50km时乙车行驶了小时
其中正确的说法有( )
 A、1个 B、2个 C、3个 D、4个5. 直线y=k1x+b1(k1>0)与y=k2x+b2(k2<0)相交于点(﹣3,0),且两直线与y轴围成的三角形面积为12那么b2﹣b1的值为( )A、3 B、8 C、﹣6 D、﹣86. 如图所示,四边形OABC为正方形,OA=8,D是AB上的一点,且BD= ,N是AC上的一动点,当△BDN的周长最小时,点N的 坐标为( )
A、1个 B、2个 C、3个 D、4个5. 直线y=k1x+b1(k1>0)与y=k2x+b2(k2<0)相交于点(﹣3,0),且两直线与y轴围成的三角形面积为12那么b2﹣b1的值为( )A、3 B、8 C、﹣6 D、﹣86. 如图所示,四边形OABC为正方形,OA=8,D是AB上的一点,且BD= ,N是AC上的一动点,当△BDN的周长最小时,点N的 坐标为( )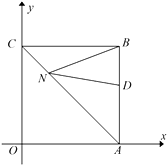 A、(6,2) B、(5,3) C、(4,4) D、7. 甲、乙两个工程队完成某项工程,首先甲队单独做了10天,然后乙队加入合作,完成剩下的全部工程.设工程总量为单位1,工程进度满足下图所示的函数关系,那么实际完成这项工程所用的时间比由甲队单独完成这项工程所需时间少( )
A、(6,2) B、(5,3) C、(4,4) D、7. 甲、乙两个工程队完成某项工程,首先甲队单独做了10天,然后乙队加入合作,完成剩下的全部工程.设工程总量为单位1,工程进度满足下图所示的函数关系,那么实际完成这项工程所用的时间比由甲队单独完成这项工程所需时间少( ) A、12天 B、14天 C、16天 D、18天8. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,直线与x轴交于点C,与y轴交于点B,若线段上的点D到直线的距离长为3,则点D的坐标为( )
A、12天 B、14天 C、16天 D、18天8. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,直线与x轴交于点C,与y轴交于点B,若线段上的点D到直线的距离长为3,则点D的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,一次函数y=-x+3的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为.
 10. 如图,一次函数y=-x+1的图象与 轴、 轴分别交于点 ,点 在 轴上,要使 是以AB为腰的等腰三角形,那么点 的坐标是.
10. 如图,一次函数y=-x+1的图象与 轴、 轴分别交于点 ,点 在 轴上,要使 是以AB为腰的等腰三角形,那么点 的坐标是. 11.
11.如图,在平面直角坐标系中,矩形AOBC的顶点A,B的坐标分别是A(0,4),B(4 , 0),作点A关于直线y=kx(k>0)的对称点P,△POB为等腰三角形,则点P的坐标为
 12. 某班带队到展览馆参观,并要求作好记录,小亮随队伍步行一段时间后,发现未带笔记本,随即跑步返回拿到笔记本后又以相同的速度追赶队伍,恰好与队伍在同一时间到达展览馆.行程与时间的关系如图所示,其中实线表示队伍的图象,虚线表示小亮的图象,则小亮跑步的速度为米/分钟.
12. 某班带队到展览馆参观,并要求作好记录,小亮随队伍步行一段时间后,发现未带笔记本,随即跑步返回拿到笔记本后又以相同的速度追赶队伍,恰好与队伍在同一时间到达展览馆.行程与时间的关系如图所示,其中实线表示队伍的图象,虚线表示小亮的图象,则小亮跑步的速度为米/分钟. 13. 如图,△ECF中∠ECF=90°,点C(-3,3),CE交x轴负半轴于点A,CF交y轴负半轴于点B,则OA-OB的值为 .
13. 如图,△ECF中∠ECF=90°,点C(-3,3),CE交x轴负半轴于点A,CF交y轴负半轴于点B,则OA-OB的值为 .
三、解答题
-
14. 某运输公司托运行李费的标准如下:当行李质量不超过20千克时就免费托运;当超过20千克,每超过1千克,则要交托运费0.5元.若王先生托运行李的质量为x(千克)(x>20),所付的托运费为y元,则:(1)、写出托运费y与行李质量x之间的函数表达式,并判断此表达式属于何种函数;(2)、若王先生行李质量为50千克,则他应交多少元托运费?(3)、如果王先生交了10元托运费,那么他的行李有多重?15. 某种机器油箱容量为 , 工作前先将空油箱加满,然后停止加油立即开始工作.下表记录了整个过程60分钟内5个时刻的油箱里的油量.其中(单位:L)表示油箱里的油量,(单位:)表示时间 .
10
20
40
50
60
30
25
15
10
5
 (1)、在平面直角坐标系中描出表中数据对应点,再选出最符合实际的函数模型,求出机器工作时关于的函数解析式,并写出自变量的取值范围.(2)、求出油箱中油量为时的值.16. 市场上甲种商品的采购价为60元/件,乙种商品的采购价为100元/件,某商店需要采购甲、乙两种商品共15件,且乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品 件( >0),购买两种商品共花费 元.(1)、求出 与 的函数关系式(写出自变量 的取值范围);(2)、试利用函数的性质说明,当采购多少件甲种商品时,所需要的费用最少?17. 为了响应国家提倡的“节能环保”号召,某公司研发出一款新能源纯电动车,如图是这款电动车充满电后,蓄电池剩余电量(千瓦时)关于已行驶路程(千米)的函数图象.
(1)、在平面直角坐标系中描出表中数据对应点,再选出最符合实际的函数模型,求出机器工作时关于的函数解析式,并写出自变量的取值范围.(2)、求出油箱中油量为时的值.16. 市场上甲种商品的采购价为60元/件,乙种商品的采购价为100元/件,某商店需要采购甲、乙两种商品共15件,且乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品 件( >0),购买两种商品共花费 元.(1)、求出 与 的函数关系式(写出自变量 的取值范围);(2)、试利用函数的性质说明,当采购多少件甲种商品时,所需要的费用最少?17. 为了响应国家提倡的“节能环保”号召,某公司研发出一款新能源纯电动车,如图是这款电动车充满电后,蓄电池剩余电量(千瓦时)关于已行驶路程(千米)的函数图象.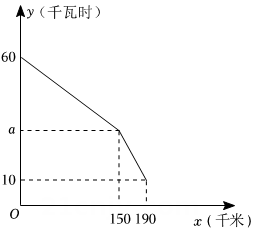 (1)、当时,1千瓦时的电量新能源纯电动车能行驶的路程为5千米,则;(2)、当时,求关于的函数表达式;(3)、请计算当新能源纯电动车已行驶160千米时,蓄电池的剩余电量.18. 某车间有50名工人,每人每天可加工16个甲种零件或15个乙种零件,安排其中一部分工人加工甲种零件,其余工人加工乙种零件,已知每加工一个甲种零件可获利20元,每加工一个乙种零件可获利24元.(1)、若该车间某天获利17000元,问这天加工甲种零件的工人多少人?(2)、由于生产需要,每天都需要加工两种零件,设加工甲种零件的人数为m .
(1)、当时,1千瓦时的电量新能源纯电动车能行驶的路程为5千米,则;(2)、当时,求关于的函数表达式;(3)、请计算当新能源纯电动车已行驶160千米时,蓄电池的剩余电量.18. 某车间有50名工人,每人每天可加工16个甲种零件或15个乙种零件,安排其中一部分工人加工甲种零件,其余工人加工乙种零件,已知每加工一个甲种零件可获利20元,每加工一个乙种零件可获利24元.(1)、若该车间某天获利17000元,问这天加工甲种零件的工人多少人?(2)、由于生产需要,每天都需要加工两种零件,设加工甲种零件的人数为m .①请用含m的式子表示该车间每天的获利w(元);
②若 , 求当m为何值时,该车间一天的获利w最大?最大为多少元?