四川省内江市第一中学2024-2025学年九年级上学期开学考试数学试题

试卷更新日期：2024-09-23 类型：开学考试

进入出卷网下载

一、单选题（每小题4分，共48分）

1. 在 $\frac{a}{4}, \frac{4}{a}, \frac{n + m}{3}, \frac{1}{m + n}, \frac{x + 5}{x}, \frac{1}{5 x^{2} - y}$ 中，分式有（）

A、2 B、3 C、4 D、5

查看试题解析
2. 人体中红细胞的直径约为 $0.0000077 m$ ， $0.0000077$ 用科学记数法表示是（）

A、 $0.77 \times 1 0^{- 5}$ B、 $0.77 \times 1 0^{- 6}$ C、 $7.7 \times 1 0^{- 5}$ D、 $7.7 \times 1 0^{- 6}$

查看试题解析
3. 下列计算正确的是（）

A、 $a^{2} \div \frac{1}{a} = a^{3}$ B、 $\frac{1}{2 a} + \frac{1}{3 a} = \frac{1}{5 a}$ C、 $\frac{1}{a} - \frac{1}{b} = \frac{a - b}{a b}$ D、 $a \div b \cdot \frac{1}{b} = a$

查看试题解析
4. 函数y= $\frac{\sqrt{x - 1}}{x - 1}$ 中，自变量x的取值范围为（　　）

A、 $x \neq 1$ B、 $x \leq 1$ C、 $x \geq 0$ 且 $x \neq 1$ D、 $x > 1$

查看试题解析
5. 选项中的曲线不能表示y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
6. 某班七个合作学习小组人数如下：5，5，6， $x$ ， 6，7，8，已知这组数据的平均数为6，则这组数据的中位数和众数是（）

A、6，5 B、6，6 C、 $7.5$ 和6 D、 $6.5$ 和6

查看试题解析
7. 如图，在矩形 $A B C D$ 中， $A B = 8$ ， $B C = 4$ ，将矩形沿 $A C$ 折叠，点D落在点 $D^{'}$ 处，则重叠部分 $△ A F C$ 的面积为（）

A、6 B、8 C、10 D、12

查看试题解析
8. 函数 $y = x + a$ 和 $y = a x$ 在同一坐标系中的图像大致是（）

A、 B、 C、 D、

查看试题解析
9. 若关于x的方程 $\begin{array}{l} \frac{x}{x - 1} - \end{array} 2 =$ $\begin{array}{l} \frac{3 m}{2 x - 2} \end{array}$ 的解为正数，则m的取值范围是（）

A、 $\begin{array}{l} m ＞ - \frac{2}{3} \end{array}$ B、 $\begin{array}{l} m ＜ \frac{4}{3} \end{array}$ C、 $m \begin{array}{l} ＞ - \frac{2}{3} \end{array}$ 且 $m \neq 0$ D、 $m \begin{array}{l} ＜ \frac{4}{3} \end{array}$ 且 $m \begin{array}{l} \neq \frac{2}{3} \end{array}$

查看试题解析
10. 已知四边形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点O， $A D ∥ B C$ ，下列判断错误的是（）

A、如果 $A B = C D$ ， $A C = B D$ ，那么四边形 $A B C D$ 是矩形 B、如果 $A B ∥ C D$ ， $O A = O B$ ，那么四边形 $A B C D$ 是矩形 C、如果 $A D = B C$ ， $A C ⊥ B D$ ，那么四边形 $A B C D$ 是菱形 D、如果 $O A = O C$ ， $A C ⊥ B D$ ，那么四边形 $A B C D$ 是菱形

查看试题解析
11. 一次函数 $y_{1} = k x + b$ 与 $y_{2} = x + a$ 的图象如图所示，则下列结论：
① $k < 0$ ， ② $a b < 0$ ；③ $y_{1}$ 随 $x$ 的增大而增大；④当 $x < 3$ 时， $y_{1} > y_{2}$ ；⑤ $3 k + b = 3 + a$ ；其中正确的个数是（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
12. 如图①， $▱ A B C D$ 中， $A B = 4 cm$ ， $∠ D = 150 °$ ，两动点M，N同时从点A出发，点M在边 $A B$ 上以 $2 cm/s$ 的速度匀速运动，到达点B时停止运动，点N沿A→D→C→B的路径匀速运动，到达点B时停止运动． $△ A M N$ 的面积 $S ({cm}^{2})$ 与点N的运动时间t（s）的关系图象如图②所示．有下列说法：
①点N的运动速度是 $1cm/s$ ；
② $A D$ 的长度为 $3 cm$ ；③a的值为7；
④当 $S = 1 {cm}^{2}$ 时，t的值为 $\sqrt{2}$ ．
其中正确的个数（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（每小题4分，共16分）

13. 平面直角坐标系中，若点 $A (a - 2, a + 1)$ 在y轴上，则点A的坐标为．

查看试题解析
14. 若点 $A {(x_{1}, y)}_{1}, B (x_{2}, y_{2}), C (x_{3}, y_{3})$ 都在反比例函数 $y = \frac{k^{2} + 1}{x}$ 的图象上，若 $x_{1} < x_{2} < 0 < x_{3}$ 则 $y_{1}, y_{2}, y_{3}$ 的大小关系是．（请用“ $<$ ”号连接）

查看试题解析
15. 如图，在 $Rt △ A B C$ 中， $A C = 6 ， B C = 8 ， ∠ C = 90 °$ ，在边 $A B 、 B C 、 A C$ 上分别取点D、E、F使四边形 $D E C F$ 为矩形，则对角线 $E F$ 的长能取到的所有整数值是．

查看试题解析
16. 如图，点 $O$ 是矩形 $A B C D$ 的对称中心，点 $P$ ， $Q$ 分别在边 $A D$ ， $B C$ 上，且 $P Q$ 经过点 $O$ ， $A B = 6$ ， $A P = 3$ ， $B C = 8$ ，点 $E$ 是边 $A B$ 上一动点．则 $△ E P Q$ 周长的最小值为．

查看试题解析

三、解答题

17. 计算：

(1)、 $3 - {(- \frac{1}{2})}^{- 2} + {(\sqrt{6} - 1)}^{0}$ ．

(2)、化简： $(1 - \frac{1}{x + 3}) \div \frac{x^{2} + 4 x + 4}{x + 3}$ ．

查看试题解析
18. 如图所示，在▱ $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，过点 $O$ 任作一条直线分别交 $A B$ ， $C D$ 于点 $E$ ， $F$ ．

(1)、求证： $O E = O F$ ；

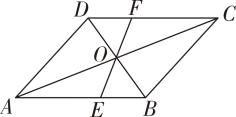(2)、连接 $A F$ ， $C E$ 直接写出当 $E F$ 与 $A C$ 满足什么关系时，四边形 $A E C F$ 是菱形？

查看试题解析
19. 某中学举行“中国梦．校园好声音”歌手大赛，八（1）、八（2）班根据初赛成绩，两个班各选出的5名选手的决赛成绩如图表．

平均数/分
中位数/分
众数/分
八（1）
a
85
c
八（2）
85
b
100

(1)、写出上表中a、b、c的值；

(2)、结合两个班成绩的平均数和中位数，分析哪个班的决赛成绩较好？

(3)、计算两个班决赛成绩的方差，并判断哪个班代表队选手的成绩较为稳定．

查看试题解析
20. 某校八年级准备购买一批笔记本奖励优秀学生，在购买时发现，每本笔记本可以打九折，用360元钱购买的笔记本，打折后购买的数量比打折前多10本．

(1)、求打折前每本笔记本的售价是多少元？

(2)、由于考虑学生的需求不同，学校决定购买笔记本和笔袋共90件，笔袋每个原售价为6元，两种物品都打九折，若购买总金额不低于360元，且不超过365元，问有哪几种购买方案？

(3)、哪种购买方案花费最少？并算出最少花费．

查看试题解析
21. 如图，已知一次函数 $y_{1} = k x + b$ 与反比函数 $y_{2} = \frac{m}{x}$ 的图象在第一、三象限分别交于 $A (6, 1)$ 、 $B (a, - 3)$ 两点，连接 $O A 、 O B$ ．

(1)、求一次函数和反比例函数的解析式；

(2)、求ΔAOB的面积；

(3)、直接写出 $y_{1}$ ≥ $y_{2}$ 时，x的取值范围．

查看试题解析
22. 在菱形 $A B C D$ 中， $∠ A B C = 60 ° ， P$ 是直线 $B D$ 上一动点，以 $A P$ 为边向右侧作等边 $△ A P E (A, P, E$ 按逆时针排列)，点 $E$ 的位置随点 $P$ 的位置变化而变化．

(1)、如图1，当点 $P$ 在线段 $B D$ 上，且点 $E$ 在菱形 $A B C D$ 内部或边上时，连结 $C E$ ，小明通过连接 $A C$ 后证明得到 $B P$ 与 $C E$ 的数量关系是______________；

(2)、如图2，当点 $P$ 在线段 $B D$ 上，且点 $E$ 在菱形 $A B C D$ 外部时，(1)中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由；

(3)、当点 $P$ 在 $B D$ 的延长线上时，其他条件不变，连接 $B E$ ，若 $A B = 2 \sqrt{3}$ ， $B E = 2 \sqrt{19}$ ，求 $P B$ 的长．

查看试题解析

	平均数/分	中位数/分	众数/分
八（1）	a	85	c
八（2）	85	b	100