【导学精练】初中数学七年级上册专题2.8.有理数的巧算（浙教版）-在线组卷题库

1. 计算： $- 3.19 + 2 \frac{19}{21} + (- 6.81) - (- 2 \frac{2}{21})$

查看试题解析
2. 计算：

(1)、 $1 \frac{3}{7} +$ $(- 2 \frac{1}{3})$ $+ 2 \frac{4}{7} +$ $(- 1 \frac{2}{3})$ ；

(2)、 $(- 1.25) + 2.25 + 7.75 + (- 8.75)$ ．

查看试题解析
3. 计算： $(- 2 \frac{1}{8}) + (+ 5) + (- 3 \frac{1}{2}) + (+ 1.125) + (+ 4 \frac{1}{2})$ ．

查看试题解析

4. 阅读下面文字：对于 $(- 5 \frac{5}{6}) + (- 9 \frac{2}{3}) + 17 \frac{3}{4} + (- 3 \frac{1}{2})$ ，可以按如下方法计算：
原式 $= [(- 5) + (- \frac{5}{6})] + [(- 9) + (- \frac{2}{3})] + (17 + \frac{3}{4}) + [(- 3) + (- \frac{1}{2})]$
$= [（ - 5 ） + （ - 9 ） + 17 + （ - 3 ）] + [(- \frac{5}{6}) + (- \frac{2}{3}) + \frac{3}{4} + (- \frac{1}{2})]$
$= 0 + (- 1 \frac{1}{4})$
$= - 1 \frac{1}{4}$ ．
上面这种方法叫拆项法．仿照上面的方法，请你计算：

(1)、 $(+ 35 \frac{7}{9}) + (- 23 \frac{4}{9})$ ；

(2)、 $(- 2018 \frac{5}{6}) + (- 2017 \frac{2}{3}) + (- 1 \frac{1}{2}) + 4036$ ．

查看试题解析
5. 计算： $- 5 \frac{5}{6} + (- 9 \frac{2}{3}) + 17 \frac{3}{4} + (- 3 \frac{1}{2})$

查看试题解析
6. 计算：

(1)、 $(+ 17 \frac{2}{5}) + (- 7 \frac{3}{5})$ ．

(2)、 $(- 2023 \frac{2}{9}) + (- 2024 \frac{4}{9}) + 4048 + \frac{5}{9}$ ．

查看试题解析

7. 计算 $1 + 2 - 3 - 4 + 5 + 6 - 7 - 8 + \dots + 2017 + 2018 - 2019 - 2020$ 值为（）

A、0 B、﹣1 C、2020 D、-2020

查看试题解析
8. 计算：

(1)、 $(- 18) + 17 + (- 12) - (- 33)$ ．

(2)、 $(+ 3 \frac{2}{5}) + (- 2 \frac{7}{8}) - (- 5 \frac{3}{5}) - (+ 1 \frac{1}{8})$ ．

查看试题解析
9. $1 - 3 - 5 + 7 + 9 - 11 - 13 + 15 + \dots + 2009 - 2011 - 2013 + 2015$

查看试题解析
10. 计算：
$2023 - 2020 + 2017 - 2014 + 2011 - 2008 + \dots \dots + 16 - 13 + 10 - 7 + 4$

查看试题解析

11. 计算：

(1)、 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{2004 \times 2005}$ ；

(2)、 $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \dots + \frac{1}{49 \times 51}$ ；

(3)、 $\frac{1}{6} + \frac{1}{12} + \frac{1}{20} + \frac{1}{30} + \frac{1}{42} + \frac{1}{56}$ ．

查看试题解析
12. 计算： $\frac{1}{2 \times 4} + \frac{1}{4 \times 6} + \frac{1}{6 \times 8} + \cdot \cdot \cdot + \frac{1}{2022 \times 2024}$ ．

查看试题解析
13. 计算： $(1 - \frac{1}{2^{2}}) \times (1 - \frac{1}{3^{2}}) \times \cdot \cdot \cdot \times (1 - \frac{1}{2021^{2}}) \times (1 - \frac{1}{2022^{2}})$ ．

查看试题解析

14. 计算： $38 \times \frac{1}{4} + 17 \times 0.25 + 45 \times 25 %$

查看试题解析
15. 计算： $8 \times (- \frac{5}{3}) \times (- 0.25) \div (- \frac{5}{6})$ ；

查看试题解析
16. 计算： $(- 0.25) \times [(- 3) \times 8 \times (- 40) \times (- \frac{1}{3})] \times 12.5$

查看试题解析
17. 计算：

(1)、 $(- 3) \div (- 1 \frac{3}{4}) \times 0.75 \div (- \frac{3}{7}) \times (- 6)$ ；

(2)、 $(- \frac{1}{5}) \times (- 0.1) \div \frac{1}{25} \times (- 10)$ ；

查看试题解析

18. 计算 $(- \frac{1}{12}) \div (\frac{1}{3} - \frac{1}{4} + \frac{1}{6})$ 的值．

查看试题解析
19. 计算： $（ - \frac{7}{8} ） \div （ 1 \frac{3}{4} - \frac{7}{8} + \frac{7}{12} ）$ ．

查看试题解析
20. 计算： $50 \div (\frac{1}{3} - \frac{1}{4} + \frac{1}{12})$ ．

查看试题解析

21. 计算： $1 - 5 + 5^{2} - 5^{3} + 5^{4} - 5^{5} + \dots + 5^{2020} - 5^{2021} + 5^{2022} - \frac{5^{2023}}{6} =$ .

查看试题解析
22. 计算： $1 + 2 + 2^{2} + 2^{3} + 2^{4} + \dots + 2^{999}$

查看试题解析
23. 计算

(1)、 $1 + 7 + 7^{2} + 7^{3} + \dots \dots + 7^{2022}$ 的值．

(2)、 $1 + 2 \times \frac{1}{3} + 3 \times {(\frac{1}{3})}^{2} + 4 \times {(\frac{1}{3})}^{3} + \dots + 9 \times {(\frac{1}{3})}^{8} + 10 \times {(\frac{1}{3})}^{9}$ ．

查看试题解析

24. 计算： $36.2 \times 1.638 + {6.38}^{2}$ ．

查看试题解析
25. 用简便方法计算

(1)、 $6 \frac{35}{36} \times (- 6)$

(2)、 $999 \times 118 \frac{4}{5} + 333 \times (- \frac{3}{5}) - 999 \times 18 \frac{3}{5}$ .

查看试题解析
26. 简便计算：

(1)、 $\frac{1^{2} + 2^{2}}{1 \times 2} + \frac{2^{2} + 3^{2}}{2 \times 3} + \frac{3^{2} + 4^{2}}{3 \times 4} + \dots + \frac{2022^{2} + 2023^{2}}{2022 \times 2023}$ ；

(2)、 $(\frac{1}{9} + \frac{1}{10} + \frac{1}{11} + \frac{1}{12}) \times (\frac{1}{10} + \frac{1}{11} + \frac{1}{12} + \frac{1}{13}) - (\frac{1}{9} + \frac{1}{10} + \frac{1}{11} + \frac{1}{12} + \frac{1}{13}) \times (\frac{1}{10} + \frac{1}{11} + \frac{1}{12})$ ．

查看试题解析
27. 怎样简便怎样算

(1)、 $2021 \times 20222022 - 2022 \times 20212021$ ；

(2)、 $1 \frac{1}{2} + 2 \frac{1}{4} + 3 \frac{1}{8} + 4 \frac{1}{16} + 5 \frac{1}{32} + 6 \frac{1}{64}$

(3)、 $\frac{2015 + 2016 \times 2014}{2016 \times 2015 - 1}$

(4)、 $(\frac{9}{20} - \frac{11}{30} + \frac{13}{42} - \frac{15}{56} + \frac{17}{72}) \times \frac{121212}{131313}$

查看试题解析

28. 看图填空：如图，把一个面积为1的正方形等分成两个面积为 $\frac{1}{2}$ 的长方形，接着把面积为 $\frac{1}{2}$ 的长方形等分成两个面积为 $\frac{1}{4}$ 的长方形，再把面积为 $\frac{1}{4}$ 的长方形等分成面积为 $\frac{1}{8}$ 的长方形，如此进行下去……

(1)、试利用图形揭示的规律计算： $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} + \frac{1}{256} + \dots \frac{1}{2^{n}}$ ＝ ▲ ．
并使用代数方法证明你的结论．

(2)、请给利用图（2），再设计一个能求： $\frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + \frac{1}{2^{4}} + \dots + \frac{1}{2^{n}}$ 的值的几何图形．

查看试题解析
29. 数和形是数学的两个主要研究对象，我们经常运用数形结合、数形转化的方法解决一些数学问题．下面我们来探究“由数思形，以形助数”的方法在解决代数问题中的应用．
如图，将一个边长为1的正方形纸片分割成7个部分，部分①是边长为1的正方形纸片面积的一半，部分②是部分①面积的一半，部分③是部分②面积的一半，依次类推．

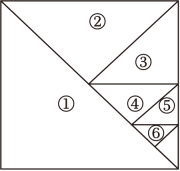(1)、图中阴影部分的面积为；

(2)、受此启发，得到 $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ⋯ + \frac{1}{2^{6}}$ ＝；

(3)、联系拓广，得到 $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ⋯ + \frac{1}{2^{n}}$ ＝（用含n的式子表示）；

(4)、迁移应用：得到 $\frac{2}{3} + \frac{1}{3} \times \frac{2}{3} + \frac{1}{3^{2}} \times \frac{2}{3} + \frac{1}{3^{3}} \times \frac{2}{3} + ⋯ + \frac{1}{3^{2023}} \times \frac{2}{3}$ ＝（直接写出答案即可）．

查看试题解析
30. 【阅读】求值 $1 + 2 + 2^{2} + 2^{3} + 2^{4} + \dots + 2^{10}$ ．

(1)、【运用】仿照此法计算：
解：设 $S = 1 + 2 + 2^{2} + 2^{3} + 2^{4} + \dots + 2^{10}$ ①
将等式①的两边同时乘以2得： $2 S = 2 + 2^{2} + 2^{3} + 2^{4} + 2^{5} + \dots + 2^{11}$ ②
由② $-$ ①得： $2 S - S = 2^{11} - 1$ ，
即： $S = 1 + 2 = 2^{2} + 2^{3} + 2^{4} + \dots + 2^{10} = 2^{11} - 1$ ，
$1 + 5 + 5^{2} + 5^{3} + 5^{4} + \dots + 5^{50}$ ；

(2)、【延伸】如图，将边长为1的正方形分成 $4$ 个完全一样的小正方形，得到左上角一个小正方形为 $S_{1}$ ，选取右下角的小正方形进行第二次操作，又得到左上角更小的正方形 $S_{2}$ ，依次操作 $2022$ 次，依次得到小正方形 $S_{1} 、 S_{2} 、 S_{3} 、 \dots 、 S_{2022}$ ．
完成下列问题：①小正方形 $S_{2022}$ 的面积等于 ▲ ；②求正方形 $S_{1} 、 S_{2} 、 S_{3} 、 \dots 、 S_{2022}$ 的面积和．

查看试题解析

【导学精练】初中数学七年级上册专题2.8.有理数的巧算（浙教版）

一、凑整法

二、拆项法

三、组合法

四、裂项相消法

五、相互转化法

六、倒数法

七、错位相减法

八、利用乘法分配律进行简算

九、利用图形进行简算