广东省深圳市南山实验教育集团麒麟中学2024-2025学年八年级上学期数学开学考试试卷
试卷更新日期:2024-09-23 类型:开学考试
一、选择题(共10小题,满分30分,每小题3分)
-
1. 下列运算正确的是( )A、5a2•a=5a3 B、(a﹣1)2=a2+1 C、 D、(4a+b)(b﹣4a)=16a2﹣b22. 肥皂泡膜是人眼能够分辨的最薄的东西之一,它的平均厚度约为700纳米,已知1纳米=10﹣9米,那么700纳米用科学记数法可表示为( )A、7×10﹣8 B、7×10﹣7 C、70×10﹣8 D、0.7×10﹣73. 下列事件中是必然事件的是( )A、床前明月光 B、大漠孤烟直 C、手可摘星辰 D、黄河入海流4. 根据下列已知条件,能够画出唯一△ABC的是( )
A、AB=5,BC=6,∠A=70° B、AB=5,BC=6,AC=13 C、∠A=50°,∠B=80°,AB=8 D、∠A=40°,∠B=50°,∠C=90°5. 如图,OC平分∠AOB,CM⊥OB于点M,CM=3,则点C到射线OA的距离为( )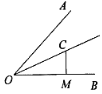 A、5 B、4 C、3 D、26.
A、5 B、4 C、3 D、26.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
 A、
A、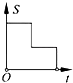 B、
B、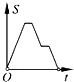 C、
C、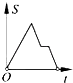 D、
D、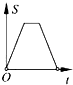 7. 如图,将一个直角三角形纸片 , 沿线段折叠,使点B落在处,若 , 则的度数为( )
7. 如图,将一个直角三角形纸片 , 沿线段折叠,使点B落在处,若 , 则的度数为( ) A、 B、 C、 D、8. 将一副直角三角板按如图所示摆放 , , , 则下列结论不正确的是( )
A、 B、 C、 D、8. 将一副直角三角板按如图所示摆放 , , , 则下列结论不正确的是( ) A、 B、 C、 D、9. 如图,△ABC的中线BD、CE相交于点O , OF⊥BC , 且BC=6,OF=2,则四边形ADOE的面积是( )
A、 B、 C、 D、9. 如图,△ABC的中线BD、CE相交于点O , OF⊥BC , 且BC=6,OF=2,则四边形ADOE的面积是( ) A、3 B、6 C、9 D、1210. 如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形拼接而成的.已知 , 正方形的面积为80.连接 , 交于点 , 交于点 , 连接 . 则图中阴影部分的面积之和为( ).
A、3 B、6 C、9 D、1210. 如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形拼接而成的.已知 , 正方形的面积为80.连接 , 交于点 , 交于点 , 连接 . 则图中阴影部分的面积之和为( ). A、8 B、12 C、16 D、20
A、8 B、12 C、16 D、20二、填空题(共5小题,满分15分,每小题3分)
-
11. 已知 , 则 .12. 如图,地板上每一个小正方形除颜色外都相同,向地板上随机掷一枚石子,石子落在阴影部分的概率是 .
 13. 长方形的周长为20cm , 其中一边为xcm(其中x>0),面积为ycm2 , 则这样的长方形中y与x的关系式可以写为 .14. 如图,直线l1 , l2 , l3分别过正方形ABCD的三个顶点A , D , C , 且相互平行,若l1 , l2的距离为1,l2 , l3的距离为2,则正方形的边长为 .
13. 长方形的周长为20cm , 其中一边为xcm(其中x>0),面积为ycm2 , 则这样的长方形中y与x的关系式可以写为 .14. 如图,直线l1 , l2 , l3分别过正方形ABCD的三个顶点A , D , C , 且相互平行,若l1 , l2的距离为1,l2 , l3的距离为2,则正方形的边长为 . 15. 阅读材料:整体代值是数学中常用的方法.例如“已知3a﹣b=2,求代数式6a﹣2b﹣1的值.”可以这样解:6a﹣2b﹣1=2(3a﹣b)﹣1=2×2﹣1=3.根据阅读材料,解决问题:若x=2是关于x的一元一次方程ax+b=3的解,则代数式4a2+4ab+b2+4a+2b﹣1的值是 .
15. 阅读材料:整体代值是数学中常用的方法.例如“已知3a﹣b=2,求代数式6a﹣2b﹣1的值.”可以这样解:6a﹣2b﹣1=2(3a﹣b)﹣1=2×2﹣1=3.根据阅读材料,解决问题:若x=2是关于x的一元一次方程ax+b=3的解,则代数式4a2+4ab+b2+4a+2b﹣1的值是 .三、解答题(共7小题,满分55分)
-
16.(1)、﹣12021﹣|﹣23|﹣(2020﹣π)0+(﹣)﹣3;(2)、(﹣3xy2)2•(﹣6x2y)÷(9x4y5);(3)、(a+2b+1)(a+2b﹣1);(4)、(简便运算)899×901+1.17. 先化简,再求值:[(2a+b)2﹣(2a+b)(2a﹣b)]÷(﹣b),其中a , b满足:|a﹣1|+(b+2)2=0.18. 如图所示,已知锐角∠AOB及一点P.
 (1)、过点P作OA、OB的垂线,垂足分别是M、N;(只作图,保留作图痕迹,不写作法)(2)、猜想∠MPN与∠AOB之间的关系,并证明.19. 如图,在一条笔直的东西方向的公路上有A、B两地,相距500米,且离公路不远处有一块山地C需要开发,已知C与A地的距离为300米,与B地的距离为400米,在施工过程中需要实施爆破,为了安全起见,爆破点C周围半径260米范围内不得进入.
(1)、过点P作OA、OB的垂线,垂足分别是M、N;(只作图,保留作图痕迹,不写作法)(2)、猜想∠MPN与∠AOB之间的关系,并证明.19. 如图,在一条笔直的东西方向的公路上有A、B两地,相距500米,且离公路不远处有一块山地C需要开发,已知C与A地的距离为300米,与B地的距离为400米,在施工过程中需要实施爆破,为了安全起见,爆破点C周围半径260米范围内不得进入. (1)、山地C距离公路的垂直距离为多少米?(2)、在进行爆破时, A、B两地之间的公路是否有危险需要暂时封锁?若需要封锁,请求出需要封锁的公路长.20. 小南一家到某度假村度假.小南和妈妈坐公交车先出发,爸爸自驾车沿着相同的道路后出发.爸爸到达度假村后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往度假村(取东西的时间忽略不计).如图是他们离家的距离s(km)与小南离家的时间t(h)的关系图.请根据图回答下列问题:
(1)、山地C距离公路的垂直距离为多少米?(2)、在进行爆破时, A、B两地之间的公路是否有危险需要暂时封锁?若需要封锁,请求出需要封锁的公路长.20. 小南一家到某度假村度假.小南和妈妈坐公交车先出发,爸爸自驾车沿着相同的道路后出发.爸爸到达度假村后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往度假村(取东西的时间忽略不计).如图是他们离家的距离s(km)与小南离家的时间t(h)的关系图.请根据图回答下列问题: (1)、图中的自变量是 , 因变量是 , 小南家到该度假村的距离是 km .(2)、小南出发 小时后爸爸驾车出发,爸爸驾车的平均速度为 km/h , 图中点A表示 .(3)、小南从家到度假村的路途中,当他与爸爸相遇时,离家的距离约是 km .21. 如果一个三角形被一条线段分割成两个等腰三角形,那么这种分割叫做等腰分割,这条线段称为这个三角形的等腰分割线.如图1,当△ABD和△ACD为等腰三角形时,AD为△ABC的等腰分割线.
(1)、图中的自变量是 , 因变量是 , 小南家到该度假村的距离是 km .(2)、小南出发 小时后爸爸驾车出发,爸爸驾车的平均速度为 km/h , 图中点A表示 .(3)、小南从家到度假村的路途中,当他与爸爸相遇时,离家的距离约是 km .21. 如果一个三角形被一条线段分割成两个等腰三角形,那么这种分割叫做等腰分割,这条线段称为这个三角形的等腰分割线.如图1,当△ABD和△ACD为等腰三角形时,AD为△ABC的等腰分割线. (1)、如图2,△ABC中,∠B=2∠C , 线段AC的垂直平分线ED交AC于点D , 交BC于点E . 求证:AE是△ABC的一条等腰分割线.(2)、如图3,在△ABC中,∠A=120°,∠B=20°,∠C=40°,请你用两种不同的方法完成△ABC的等腰分割,并直接写出每种分割之后两个等腰三角形的顶角度数.(3)、在△ABC中,AD为△ABC的等腰分割线,且AD=BD , ∠C=30°,请直接写出∠B的度数.22.
(1)、如图2,△ABC中,∠B=2∠C , 线段AC的垂直平分线ED交AC于点D , 交BC于点E . 求证:AE是△ABC的一条等腰分割线.(2)、如图3,在△ABC中,∠A=120°,∠B=20°,∠C=40°,请你用两种不同的方法完成△ABC的等腰分割,并直接写出每种分割之后两个等腰三角形的顶角度数.(3)、在△ABC中,AD为△ABC的等腰分割线,且AD=BD , ∠C=30°,请直接写出∠B的度数.22. (1)、问题发现:如图1,△ABC和△DCE均为等边三角形,当△DCA旋转至点A , D , E在同一直线上,连接BE , 易证△BCE≌△ACD , 则
(1)、问题发现:如图1,△ABC和△DCE均为等边三角形,当△DCA旋转至点A , D , E在同一直线上,连接BE , 易证△BCE≌△ACD , 则①线段AD、BE之间的数量关系是 ;
②∠BEC=;
(2)、拓展研究:如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A , D , E在同一直线上,若AE=15,DE=7,求AB的长度;(3)、探究发现:如图3,点P为等边三角形ABC内一点,且∠BPC=150°,∠DPB=30°,BP=6,CP=4,DP=8,求AD的长.