【提升版】北师大版数学八年级上册4.4一次函数的应用同步练习

试卷更新日期：2024-09-23 类型：同步测试

进入出卷网下载

一、选择题

1. 若直线 $y = k_{1} x + 2$ 与直线 $y = k_{2} x - 4$ 的交点在 $x$ 轴上，则 $\frac{k_{1}}{k_{2}}$ 的值为（）

A、2 B、 $- 2$ C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 甲从深圳匀速骑电动车到广州，乙从广州匀速骑摩托车到深圳，两人同时出发，到达目的地后，立即停止运动，甲、乙两人离深圳的距离 $y (k m)$ 与他们骑车的时间 $x (h)$ 之间的函数关系如图所示，则下列说法错误的是（）

A、深广两地的距离为 $120 k m$ B、甲的速度为 $20 k m / h$ C、乙的速度为 $30 k m / h$ D、乙运动 $3 h$ 到达深圳

查看试题解析
3. 已知一次函数 $y = k x + b (k \neq 0)$ 的图象过点 $(- 2 ， 7) ， (2 ， 3)$ ，则下列结论正确的是（）

A、该函数的图象与 $x$ 轴的交点坐标是 $(2 ， 0)$ B、将该函数的图象向下平移4个单位长度得 $y = - 2 x$ 的图象 C、若点 $(1 ， y_{1}) 、 (3 ， y_{2})$ 均在该函数图象上，则 $y_{1} < y_{2}$ D、该函数的图象经过第一、二、四象限

查看试题解析
4. 甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．则下列结论：
①A，B两城相距300千米；
②乙车比甲车晚出发1小时，却早到1小时；
③乙车出发后2.5小时追上甲车；
④当甲、乙两车相距50千米时，t= $\frac{5}{4}$ 或 $\frac{15}{4}$ ．
其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 一次函数y＝2x+m的图象经过两个点A（-1，y₁）和B（2，y₂），则y₁与y₂的大小关系是（）

A、y₁＜y₂ B、y₁＞y₂ C、当m＞0时，y₁＞y₂ D、当m＜0时，y₁＞y₂

查看试题解析
6. 一次函数 $y = k x + b$ 与 $y = m x + n$ 的图象如图所示，则下列说法不正确的是（）

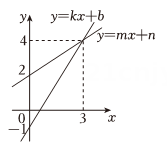A、 $b = - 1 ， n = 2$ B、这两个函数的图象与 $y$ 轴围成的三角形的面积为4. 5 C、关于 $x ， y$ 的方程组 ${\begin{array}{l} y = k x + b \\ y = m x + n \end{array}$ 的解为 ${\begin{array}{l} x = 3 \\ y = 4 \end{array}$ D、当 $x$ 从0开始增加时，函数 $y = k x + b$ 比 $y = m x + n$ 的值先达到3

查看试题解析
7. 甲无人机从地面起飞，乙无人机从距离地面20 $m$ 高的楼顶起飞，两架无人机同时匀速上升10s．甲、乙两架无人机所在的位置距离地面的高度y（单位： $m$ ）与无人机上升的时间x（单位：s）之间的关系如图所示， $10 s$ 时，两架无人机的高度差为（）

A、10 $m$ B、15 $m$ C、20 $m$ D、25 $m$

查看试题解析
8. 如图所示，已知点A坐标为 $(6 ， 0)$ ，直线 $y = x + b$ （ $b > 0$ ）与 $y$ 轴交于点 $B$ ，与 $x$ 轴交于点 $C$ ，连接 $A B$ ， $A B = 4 \sqrt{3}$ ，则 $O C$ 的长为（）

A、 $2 \sqrt{3}$ B、 $3 \sqrt{3}$ C、3 D、 $4 \sqrt{3}$

查看试题解析

二、填空题

9. 如图所示，在平面直角坐标系中，线段AB所在直线的函数表达式为y=-x+4，C是AO的中点，P是AB上一动点，则PO+PC的最小值是.

查看试题解析
10. 直线 $P Q ∥ x$ 轴，已知点 $P (5 ， - 3)$ ，则点 $Q$ 的纵坐标是．

查看试题解析
11. 声音在空气中传播的速度（简称声速） $y （ m / s ）$ 是空气温度 $t （ ℃ ）$ 的一次函数，若当空气温度为 $0 ℃$ 时，声速为 $330 m / s$ ；当空气温度为 $10 ℃$ 时，声速为 $336 m / s$ ，则声速y与温度t的函数关系式为．

查看试题解析
12. 如图1，11月10日晚，“深爱万物”—2023深圳人才嘉年华活动正式启动，千余架无人机在深圳人才公园上空上演“天空之舞”，为人才喝彩、向人才致敬．如图2的平面直角坐标系中，线段 $O A ， B C$ 分别表示1号、2号无人机在队形变换中飞行高度 $y_{1}$ ， $y_{2} (m)$ 与飞行时间 $x (s)$ 的函数关系，其中 $y_{2} = - 4 x + 150$ ，线段 $O A$ 与 $B C$ 相交于点P ， $A B ⊥ y$ 轴于点B ，点A的横坐标为25．则在第秒时1号和2号无人机在同一高度．

查看试题解析
13. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步 $500 m$ ，先到终点的人原地休息.已知甲先出发 $2 s$ .在跑步过程中，甲、乙两人的距离 $y (m)$ 与乙出发的时间 $t (s)$ 之间的关系如图所示，给出以下结论：① $a = 8$ ；② $b = 92$ ；③ $c = 123$ .其中正确的是.

查看试题解析

三、解答题

14. 某商店分两次购进 A、B两种商品进行销售，两次购进同一种商品的进价相同，具体情况如下表所示：

购进数量（件）
购进所需费用（元）
A
B
第一次
30
40
3800
第二次
40
30
3200

(1)、求A、B两种商品每件的进价分别是多少元？

(2)、商场决定A种商品以每件30元出售，B种商品以每件100元出售．为满足市场需求，需购进A、B两种商品共1000件，且A种商品的数量不少于B种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润．

查看试题解析
15. 甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（km）与甲车行驶的时间t（h）之间的函数关系如图所示．

(1)、A，B两城相距千米；

(2)、当1≤t≤4时，求乙车离开A城的距离y（km）与甲车行驶的时间t（h）之间的函数关系式；

(3)、乙车出发后小时追上甲车．

查看试题解析
16. 某通讯公司开展营销活动，设置了甲、乙两种手机资费套餐，手机资费 $y$ （元）与通话时间 $x$ （分）之间的关系如图所示．

(1)、说明线段 $A B$ 的实际意义；

(2)、求出乙套餐每月手机资费 $y$ （元）与通话时间 $x$ （分）之间的函数关系式；

(3)、结合图像，说明选择哪种手机资费套餐更合算．

查看试题解析
17. 如图，已知直线 $y = - \frac{4}{3} x + 8$ 与 $x$ 轴， $y$ 轴分别交于点 $A$ 和点 $B$ ， $M$ 为线段 $O B$ 上一点，若将 $△ A B M$ 沿 $A M$ 折叠，点 $B$ 恰好落在 $x$ 轴上的点 $B^{'}$ 处.

(1)、求 $A$ ， $B$ 两点的坐标.

(2)、求直线 $A M$ 的函数表达式.

查看试题解析
18. 如图，直线L₁： $y = - x + 2$ 与轴， $y$ 轴分别交于A，B两点，点P（ $m$ ， 3）为直线AB上一点，另一直线L₂： $y = k x + 4$ 经过点P．

(1)、求点A、B坐标；

(2)、求点P坐标和的值；

(3)、若点C是直线L₂与轴的交点，点Q是轴上一点，当△CPQ的面积等于3时，求出点Q的坐标

查看试题解析

	购进数量（件）		购进所需费用（元）
	A	B	购进所需费用（元）
第一次	30	40	3800
第二次	40	30	3200

【提升版】北师大版数学八年级上册4.4一次函数的应用 同步练习

一、选择题

二、填空题

三、解答题

【提升版】北师大版数学八年级上册4.4一次函数的应用同步练习