【导学精练】初中数学七年级上册专题2.3.有理数的乘法（浙教版）-在线组卷题库

1. 现有以下五个结论：①两个非负数的乘积一定是正数；②若两个数互为相反数，则它们相乘的积是负数；③任何一个有理数都可以在数轴上表示；④两个数的和为正数，则这两个数可能异号；⑤几个有理数相乘，负因数个数为奇数则乘积为负数，其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 若 $a b c = 0$ ，则下列选项正确的是（　　）

A、a ， b ， c没有一个为0 B、a ， b ， c只有一个为0 C、a ， b ， c至少一个为0 D、a ， b ， c三个都为0

查看试题解析
3. 下列说法中正确的有（　　）
①同号两数相乘，符号不变；②异号两数相乘，积取负号；③数a、b互为相反数，它们的积一定为负；④四个有理数相乘，若有三个负因数，则积为负。

A、1个 B、2个 C、3个 D、4个

查看试题解析

4. 下列式子中，积的符号为负的是（）

A、 $(- \frac{1}{3}) \times (+ \frac{1}{4}) \times (- 6)$ B、 $(- 9) \times (+ \frac{1}{8}) \times (- \frac{4}{7}) \times (+ 7) \times (- \frac{1}{3})$ C、 $(- 3) \times (- \frac{1}{2}) \times (+ 7) \times 0$ D、 $(- \frac{1}{5}) \times (+ 6) \times (- \frac{2}{3}) \times (- 5) \times (- \frac{1}{2})$

查看试题解析
5. 下列算式中，积为负数的是（）

A、 $0 \times (- 5)$ B、 $4 \times (- 0.2) \times (- 10)$ C、 $(- 1.5) \times (- 2)$ D、 $(- 3) \times (- \frac{1}{5}) \times (- \frac{2}{3})$

查看试题解析
6. 如图， $A ， B$ 两点在数轴上表示的数分别是 $a ， b$ ，下列式子成立的是（）

A、 $a b > 0$ B、 $a + b > 0$ C、 $(a - 1) (b + 1) < 0$ D、 $(a + 1) (b - 1) > 0$

查看试题解析

7. $(- 3) \times (- 4)$ 的值是（）

A、12 B、7 C、 $- 12$ D、 $- 7$

查看试题解析
8. 把 $- 6$ 表示成两个整数的积，共出现的可能性有（）

A、2种 B、3种 C、4种 D、5种

查看试题解析
9. 计算： $4 \times (- \frac{3}{2})$ ＝．

查看试题解析
10. 计算： $- 4 \frac{2}{3} \times (- 2 \frac{1}{7}) =$ ．

查看试题解析
11. 下列计算结果最大的是（）

A、 $(- 1) \times 3 \times 4 \times (- 2)$ B、 $(- 5) \times (- 3) \times 4 \times (- 2)$ C、 $2 \times (- 6) \times (- 8) \times (- 4)$ D、 $2024 \times (- 13) \times (- 14) \times 0$

查看试题解析

12. 阅读与思考

下面是小宇同学的数学小论文，请仔细阅读并完成相应的计算．

逆用乘法分配律解题

我们知道，乘法分配律是 $a (b + c) = a b + a c$ ，反过来 $a b + a c = a (b + c)$ ．这就是说，当 $a b + a c$ 中有相同的a时，我们可以逆用乘法分配律得到 $a b + a c = a (b + c)$ ，进而可使运算简便．例如：计算 $- \frac{5}{8} \times 23 - \frac{5}{8} \times 17$ ，若利用先乘后减显然很繁琐，注意到两项都有 $- \frac{5}{8}$ ，因此逆用乘法分配律可得 $- \frac{5}{8} \times 23 - \frac{5}{8} \times 17 = - \frac{5}{8} \times (23 + 17) = - \frac{5}{8} \times 40 = - 25$ ，这样计算就简便得多

计算：

(1)、

- 29 \times 588 + 28 \times 588

；

(2)、

- 2023 \times \frac{3}{7} + 2023 \times (- \frac{6}{7}) + 2023 \times \frac{2}{7}

；

(3)、

(- 47.65) \times 2 \frac{6}{11} + (- 37.15) \times (- 2 \frac{6}{11}) + 10.5 \times (- 7 \frac{5}{11})

．

查看试题解析

13. 用简便方法计算：

(1)、 $4 \times (- 198) \times (- 0.25) \times \frac{1}{99}$

(2)、 $(- \frac{7}{6} + \frac{3}{4} - \frac{1}{12}) \times (24)$

(3)、 $- 5 \times (- 7 \frac{1}{3}) + 7 \times (- 7 \frac{1}{3}) - (- 12) \times (- 7 \frac{1}{3})$

(4)、 $99 \frac{71}{72} \times (- 36)$

查看试题解析
14. 给下面的计算过程标明理由：
$(- 36) \times (\frac{1}{3} - \frac{4}{9} + \frac{5}{12} - \frac{3}{4})$
$= (- 36) \times \frac{1}{3} + 36 \times \frac{4}{9} - 36 \times \frac{5}{12} + 36 \times \frac{3}{4}$ （                 ）
$= - 12 + 16 - 15 + 27$ （                 ）
$= - 12 - 15 + 16 + 27$ （                 ）
$= (- 12 - 15) + (16 + 27)$
$= - 27 + 43$

查看试题解析
15. 计算：

(1)、 $(- \frac{9}{4}) \times (- 2.3) \times (+ \frac{8}{9})$

(2)、 $(\frac{7}{9} - \frac{5}{12} + 2 - \frac{11}{6}) \times (- 36)$

(3)、 $- 8 \times (- \frac{15}{29}) + 12 \times (- \frac{15}{29}) - 4 \times (- \frac{15}{29})$

查看试题解析

16. 某工艺坊加工一件艺术品，完成该任务共需 $A$ ， $B$ ， $C$ ， $D$ ， $E$ ， $F$ 六道工序，其中 $A$ ， $B$ 是前期准备阶段， $C$ ， $D$ ， $E$ 是中期制作阶段， $F$ 为最后的扫尾阶段，三个阶段不能改变顺序，也不能同时进行，但各阶段内的几个工序可以同时进行，完成各道工序所需时间如下表所示：
阶段
准备阶段
中期制作阶段
扫尾阶段
工序
$A$
$B$
$C$
$D$
$E$
$F$
所需时间/分钟
$11$
$15$
$20$
$17$
$6$
$3$
加工时间每缩短一分钟需要增加投入费用/元
$100$
$70$
$100$
$80$
$50$
不能缩短
在不考虑其它因素的前提下，加工该件艺术品最少需要分钟；现因情况有变，需将加工时间缩短到 $30$ 分钟．每道工序加工时间每缩短一分钟需要增加投入费用如上表，则所增加的投入最少是元．

查看试题解析
17. 萧红中学九年级12支班级篮球队预计在三月份举行校级篮球友谊赛，球队进行单循环比赛（参加比赛的每两支球队之间都要进行一场比赛），则总的比赛场数为场．

查看试题解析
18. 如图，一玻璃柜的主视图形状是长（AB）1.5米、宽（BC）1米的矩形，现在需要在木框架间嵌入玻璃，已知木框架宽为0.1m，则需要的玻璃总面积为平方米．

查看试题解析

19. 根据以下素材，探索完成任务．

如何规划游玩路线？
素材1	温州轨道交通实行里程分段计价票制，起步价 $2$ 元，可乘坐 $4 k m$ （含 $4 k m$ ）， $4$ 至 $28 k m$ （含 $28 k m$ ）每 $1$ 元可乘 $4 k m$ （不足 $4 k m$ 按 $1$ 元算）．如：桐岭站到动车南站共 $5.3 k m$ ，收费 $3$ 元．部分站点距离见下图（单位： $k m$ ）
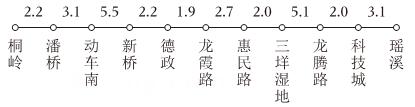
素材2	一名成年乘客可免费携带一名身高不足 $1.2$ 米（含 $1.2$ 米）的儿童乘车．
素材3	小明一家四口将乘坐轻轨出游．小明家住在新桥站附近，家庭成员如下：小明（身高 $1.5$ 米）、弟弟（身高 $1.1$ 米）、爸爸、妈妈．
问题解决
分析规划	任务1	从新桥站到桐岭站为 ▲ $k m$ ，单人单程乘坐需车费 ▲ 元．
	任务2	小明一家乘坐轻轨从新桥站到三垟湿地站，需要多少车费．
确定方案	任务3	小明一家从新桥站出发，计划共用 $30$ 元车费出行（往返），请你为小明一家规划一个尽可能远的游玩站点，并说明理由．

查看试题解析

20. 规定 $a \otimes b = a b - 1$ ，则 $(- 2) \otimes (- 3) \otimes (- 4)$ 的值等于（）

A、5 B、 $- 21$ C、 $- 7$ D、 $- 21$ 或 $- 7$

查看试题解析
21. 若定义一种新运算，规定 $|\begin{array}{l} a & b \\ c & d \end{array}| = a d - b c$ ，则 $|\begin{array}{l} - 1 & - 2 \\ 3 & 4 \end{array}| =$ ．

查看试题解析
22. 定义一种新运算“ $\otimes$ ”，规定： $a \otimes b = 2 a - 3 b$ 等式右边的运算就是加、减、乘、除四则运算，例如： $2 \otimes (- 3) = 2 \times 2 - 3 \times (- 3) = 4 + 9 = 13$ ， $1 \otimes 2 = 2 \times 1 - 3 \times 2 = 2 - 6 = - 4$ ．则 $(- 1) \otimes [3 \otimes (- 2)]$ 的值是（）．

A、 $- 2$ B、 $- 18$ C、 $- 28$ D、 $- 38$

查看试题解析
23. 小尚同学与小志同学约定了一种新运算：对于任意有理数 $a$ 和 $b$ ，规定 $a ☆ b = a b (b + 1)$ ．小尚同学尝试计算 $2 ☆ (- 3) = 2 \times (- 3) \times [(- 3) + 1] = 12$ ，现在请小志同学计算 $(- 2) ☆ 7 =$ ．

查看试题解析
24. 记符号 $[x]$ 表示不超过x的最大整数，如 $[3] = 3$ ， $[2.9] = 2$ ， $[- 1.5] = - 2$ ．

(1)、分别写出 $[4]$ 和 $[- 2.1]$ 的值；

(2)、计算： $[- 0.2] \times [4.5] \times [- 3]$ ．

查看试题解析

25. 2023年5月24日全球贸易投资促进峰会在北京举行，本次峰会主题为“坚定信心合作共赢，共建开放型世界经济”，那么2023的相反数的倒数是（　　）

A、 $\frac{1}{2023}$ B、 $- 2023$ C、 $- \frac{1}{2023}$ D、2023

查看试题解析
26. 如果a大于b ，那么a的倒数小于b的倒数，下列举例能说明这种说法错误的是（）

A、 $a = 2, b = 1$ B、 $a = - 2, b = - 1$ C、 $a = 2, b = - 1$ D、 $a = \frac{1}{2}, b = \frac{1}{3}$

查看试题解析
27. 下列语句说法正确的个数是（）

(1)、几个数相乘，积的符号与负因数的个数有关，当负因数为奇数个时，积为负，当负因数为偶数个时，积为正．（2）除以一个数等于乘以这个数的倒数．（3）加上一个数等于减去这个数的相反数．（4）如果a大于b ，那么a的倒数大于b的倒数．（5）一个数大于另一个数的绝对值，则这个数一定是正数

A、1个 B、2个 C、3个 D、4个

查看试题解析
28. 做一做：
①5的倒数是； ② $2 \frac{2}{3}$ 的倒数是； ③ $0.1$ 的倒数是；
④ $- 3.75$ 的倒数是； ⑤ $- 3$ 的倒数是； ⑥ $- 0.15$ 的倒数是．

查看试题解析
29. 下列说法正确的是（）

A、两个正数互为倒数，其中一个数必大于1 B、一个假分数的倒数一定小于本身 C、若一个数的倒数是它本身，那么这个数一定是1 D、若两个数互为倒数，那么它们的积一定是1

查看试题解析
30. 若 $m n = 1$ ，则下列说法正确的是（）

A、 $m$ 与 $n$ 互为倒数 B、 $m$ 与 $n$ 互为相反数 C、 $m$ 与 $n$ 相等 D、 $| m |$ 与 $| n |$ 相等

查看试题解析

【导学精练】初中数学七年级上册专题2.3.有理数的乘法（浙教版）

一、有理数乘法法则的辨析

二、利用有理数乘法的符号辨别

三、有理数的乘法运算

四、有理数乘法运算律

五、有理数乘法的实际应用

六、有理数乘法的新定义问题

七、倒数的概念与运用

阶段	准备阶段		中期制作阶段			扫尾阶段
工序	$A$	$B$	$C$	$D$	$E$	$F$
所需时间/分钟	$11$	$15$	$20$	$17$	$6$	$3$
加工时间每缩短一分钟需要增加投入费用/元	$100$	$70$	$100$	$80$	$50$	不能缩短