【基础版】北师大版数学八年级上册4.4一次函数的应用 同步练习
试卷更新日期：2024-09-22 类型：同步测试
一、选择题
-
1. 直线的图象与轴的交点坐标为（ ）A、 B、 C、 D、2. 对于一次函数 ， 结论如下：
①函数的图象不经过第三象限；②函数的图象与x轴的交点坐标是
③将函数的图象向下平移2个单位长度可以得到的图象；
④若两点 ， 在该函数图象上，则 ． 其中正确的结论有（ ）
A、1个 B、2个 C、3个 D、4个3. 如图所示，反映了天利公司某种产品的销售收入与销售量的关系，反映了该种产品的销售成本与销售量的关系．根据图象提供信息，下列说法正确的是（ ）
A、当销售量为2吨时，销售成本是2000元 B、销售成本是5000元时，该公司的该产品盈利 C、当销售量为5吨时，该公司的该产品盈利1000元 D、的函数表达式为二、填空题
-
4. 在平面直角坐标系中，一次函数y=+1的图象与y轴交点坐标为.5. 若直线 与 轴的交点坐标为 则关于 的方程 的解是 ．6. 如图是A，B两种手机套餐每月资费y(元)与通话时间x(分钟)对应的函数图象，若小红每月通话时间大约为500分钟，则从A，B两种手机资费套餐中选择套餐更合适．
7. 在平面直角坐标系中，一次函数 与 的图象的位置关系为.8. 元旦期间，胡老师开车从扬州到相距150千米的老家探亲，如果油箱里剩余油量 y（升）与行驶里程 x（千米）之间是一次函数关系，其图象如图所示，那么胡老师到达老家时，油箱里剩余油量是升．
三、解答题
-
9. 如图，把一些相同规格的碗整齐地叠放在水平桌面上，这摞碗的高度随着碗的数量变化而变化的情况如表格所示：
碗的数量（只） 1 2 3 4 5 ······ 高度（cm） 4 5.2 6.4 7.6 8.8 ······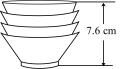 
(1)、上述两个变量之间的关系中，哪个是自变量？哪个是因变量？(2)、用h（cm）表示这摞碗的高度，用（只）表示这摞碗的数量，请用含有的代数式表示h；(3)、若这摞碗的高度为11.2cm，求这摞碗的数量.10. 如图，直线与直线相交于点 ．
(1)、求b，m的值；(2)、垂直于x轴的直线交直线于C，D两点，若线段CD长为6，求点D的坐标．11. 清德铺位于清徐县徐沟镇正南5公里，该村种植红薯由来已久，据传从清光绪时就开始享誉龙城，2018年获国家农产品地理标志登记保护.红薯丰收时节，某农户启动线上销售，每千克红薯的定价为3元，当销售量不超过10千克时，每笔订单均收取6元的快递费；当销售量超过10千克时，免快递费.设每笔线上红薯订单的销售量为千克，每笔订单的总收款额为元.
(1)、当时，与之间的函数关系式为；当时，与之间的函数关系式为；
(2)、一笔10千克的线上红薯订单，总收款额为多少元？(3)、若一笔订单的总收款额为108元，求这笔订单的销售量.12. 共享电动车是一种新理念下的交通工具：主要面向～的出行距离．现有、两种品牌的共享电动车，收费与骑行时间之间的函数关系如图所示，其中品牌收费方式对应 ， 品牌的收费方式对应 ．
(1)、品牌每分钟收费元；(2)、求品牌的函数关系式；(3)、如果小明每天早上需要骑行品牌或品牌的共享电动车去工厂上班，已知两种品牌共享电动车的平均行驶速度均为 ， 小明家到工厂的距离为 ， 那么小明选择哪个品牌的共享电动车更省钱呢？13. 已知两地相距 ， 甲、乙两人沿同一条公路从地出发匀速运动到地，先到地的人原地休息，甲开轿车，乙骑摩托车．已知乙先出发，然后甲再出发．设在这个过程中，甲、乙两人的距离与乙离开地的时间（）之间的函数关系如图所示．
(1)、第一次相遇的时间在乙出发小时．(2)、求线段对应的函数表达式．(3)、当甲、乙两人只有一人在行驶，且两人相距时，求此时乙行驶的时间．