【培优版】北师大版数学八年级上册4.3一次函数的图象 同步练习
试卷更新日期:2024-09-22 类型:同步测试
一、选择题
-
1. 如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC , 线段PC绕点P顺时针旋转90°至线段PD , 过点D作直线AB⊥x轴,垂足为B , 直线AB与直线y=x交于点A , 且BD=2AD , 连接CD , 直线CD与直线y=x交于点Q , 则点Q的坐标为( )
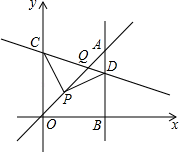 A、( , ) B、(3,3) C、( , ) D、( , )2. 定义,图象与x轴有两个交点的函数y=叫做关于直线x=m的对称函数,它与x轴负半轴交点记为A,与x轴正半轴交点记为B例如:如图:直线l:x=1,关于直线l的对称函数y=与该直线l交于点C,当直线y=x与关于直线x=m的对称函数有两个交点时,则m的取值范围是( )
A、( , ) B、(3,3) C、( , ) D、( , )2. 定义,图象与x轴有两个交点的函数y=叫做关于直线x=m的对称函数,它与x轴负半轴交点记为A,与x轴正半轴交点记为B例如:如图:直线l:x=1,关于直线l的对称函数y=与该直线l交于点C,当直线y=x与关于直线x=m的对称函数有两个交点时,则m的取值范围是( ) A、0≤m≤ B、-2<m≤ C、-2<m≤2 D、-4<m<03. 如图,在平面直角坐标系中,点P是正比例函数y=x图象上的一点,点A的坐标为(0,1),点B的坐标为(4,1),当PB-PA取最大值时,点P的坐标为( )
A、0≤m≤ B、-2<m≤ C、-2<m≤2 D、-4<m<03. 如图,在平面直角坐标系中,点P是正比例函数y=x图象上的一点,点A的坐标为(0,1),点B的坐标为(4,1),当PB-PA取最大值时,点P的坐标为( ) A、(1,2) B、(-0.5,-0.5) C、( +3, -3) D、(-2,-2)4. 甲、乙两车分别从A,B两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为 ,甲、乙两车离AB中点C的路程 千米 与甲车出发时间 时 的关系图象如图所示,则下列说法错误的是( )
A、(1,2) B、(-0.5,-0.5) C、( +3, -3) D、(-2,-2)4. 甲、乙两车分别从A,B两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为 ,甲、乙两车离AB中点C的路程 千米 与甲车出发时间 时 的关系图象如图所示,则下列说法错误的是( ) A、A,B两地之间的距离为180千米 B、乙车的速度为36千米 时 C、a的值为 D、当乙车到达终点时,甲车距离终点还有30千米5. A、B两地相距2400米,甲、乙两人从起点A地匀速步行去终点B地,已知甲先出发4分钟,在整个步行过程中,甲、乙两人之间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论中,其中正确的结论有( ):
A、A,B两地之间的距离为180千米 B、乙车的速度为36千米 时 C、a的值为 D、当乙车到达终点时,甲车距离终点还有30千米5. A、B两地相距2400米,甲、乙两人从起点A地匀速步行去终点B地,已知甲先出发4分钟,在整个步行过程中,甲、乙两人之间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论中,其中正确的结论有( ):①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
 A、1 B、2 C、3 D、46. 八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
A、1 B、2 C、3 D、46. 八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )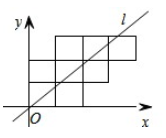 A、
A、 B、
B、 C、
C、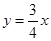 D、y=x
7. 下列对一次函数y=ax+4x+3a﹣2(a为常数,a≠﹣4)的图象判断正确的是( )A、图象一定经过第二象限 B、若a>0,则其图形一定过第四象限 C、若a>0,则y的值随x的值增大而增大 D、若a<4,则其图象过一、二、四象限8. 如图,直线y=x+2与y轴相交于点A0 , 过点A0作轴的平行线交直线y=0.5x+1于点B1 , 过点 B1作轴的平行线交直线y=x+2于点A1 , 再过点作轴的平行线交直线y=0.5x+1于点B2 , 过点 B2作轴的平行线交直线y=x+2于点A2 , …,依此类推,得到直线y=x+2上的点A1 , A2 , A3 , …,与直线y=0.5x+1上的点B1 , B2 , B3 , …,则A7B8的长为( )
D、y=x
7. 下列对一次函数y=ax+4x+3a﹣2(a为常数,a≠﹣4)的图象判断正确的是( )A、图象一定经过第二象限 B、若a>0,则其图形一定过第四象限 C、若a>0,则y的值随x的值增大而增大 D、若a<4,则其图象过一、二、四象限8. 如图,直线y=x+2与y轴相交于点A0 , 过点A0作轴的平行线交直线y=0.5x+1于点B1 , 过点 B1作轴的平行线交直线y=x+2于点A1 , 再过点作轴的平行线交直线y=0.5x+1于点B2 , 过点 B2作轴的平行线交直线y=x+2于点A2 , …,依此类推,得到直线y=x+2上的点A1 , A2 , A3 , …,与直线y=0.5x+1上的点B1 , B2 , B3 , …,则A7B8的长为( ) A、64 B、128 C、256 D、512
A、64 B、128 C、256 D、512二、填空题
-
9. 如图,直线 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为 .
 10. 一次函数y=(2m﹣6)x+5中,y随x的增大而减小,则m的取值范围是 .11. 如果不论k为何值,一次函数y= 的图象都经过一定点, 则该定点的坐标是 .12. 已知一次函数(k是常数且)的图象始终经过点 , 则a的值为 .13. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在一三象限角平分线上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn , 则第4个正方形的边长是 , Sn的值为.
10. 一次函数y=(2m﹣6)x+5中,y随x的增大而减小,则m的取值范围是 .11. 如果不论k为何值,一次函数y= 的图象都经过一定点, 则该定点的坐标是 .12. 已知一次函数(k是常数且)的图象始终经过点 , 则a的值为 .13. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在一三象限角平分线上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn , 则第4个正方形的边长是 , Sn的值为.
三、解答题
-
14. 如图,直线y=kx+b与x轴、y轴分别交于点A(4,0),B(0,4),点P在x轴上运动,连接PB,将△OBP沿直线BP折叠,点O的对应点记为0'
 (1)、填空:k=;b=。(2)、若点O'恰好落在直线AB上,求△OBP的面积;(3)、将线段PB绕点P顺时针旋转45°得到线段PB',直线PB'与直线AB的交点为Q,在点P的运动过程中,是否存在某一位置,使得△PBQ为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由。15. 如图,已知一次函数的图象与x轴交于点 , 交y轴于点B,
(1)、填空:k=;b=。(2)、若点O'恰好落在直线AB上,求△OBP的面积;(3)、将线段PB绕点P顺时针旋转45°得到线段PB',直线PB'与直线AB的交点为Q,在点P的运动过程中,是否存在某一位置,使得△PBQ为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由。15. 如图,已知一次函数的图象与x轴交于点 , 交y轴于点B, (1)、求m的值与点B的坐标;(2)、点是平面直角坐标系内一动点,若面积为12,求点P的坐标(3)、若点P在x轴上,且为等腰三角形,请直接写出点P的坐标.16. 如图,在平面直角坐标系xOy中,直线y=2x+2与y轴交于点A,与x轴交于点B.直线l⊥x轴负半轴于点C,点D是直线l上一点且位于x轴上方.已知CO=CD=4.
(1)、求m的值与点B的坐标;(2)、点是平面直角坐标系内一动点,若面积为12,求点P的坐标(3)、若点P在x轴上,且为等腰三角形,请直接写出点P的坐标.16. 如图,在平面直角坐标系xOy中,直线y=2x+2与y轴交于点A,与x轴交于点B.直线l⊥x轴负半轴于点C,点D是直线l上一点且位于x轴上方.已知CO=CD=4.
(1)、求经过A,D两点的直线的函数关系式和点B的坐标;
(2)、在直线l上是否存在点P使得△BDP为等腰三角形,若存在,直接写出P点坐标,若不存在,请说明理由.17. 在平面直角坐标系xOy中,点A、B分别在y轴和x轴上,已知点A(0,4).以AB为直角边在AB左侧作等腰直角△ABC,∠CAB=90°. (1)、当点B在x轴正半轴上,且AB=8时
(1)、当点B在x轴正半轴上,且AB=8时①求AB解析式;
②求C点坐标;
(2)、当点B在x轴上运动时,连接OC,求AC+OC的最小值及此时B点坐标.18. 如图1,在同一平面直角坐标系中,直线:与直线:相交于点 , 与x轴交于点 , 直线与轴交于点. (1)、填空: = , = , = ;(2)、如图2,点为线段上一动点,将△沿直线翻折得到△ , 线段交轴于点.
(1)、填空: = , = , = ;(2)、如图2,点为线段上一动点,将△沿直线翻折得到△ , 线段交轴于点.① 当点落在轴上时,求点的坐标;
② 若△为直角三角形,求点的坐标.