【提升版】北师大版数学八年级上册4.3一次函数的图象同步练习

试卷更新日期：2024-09-22 类型：同步测试

进入出卷网下载

一、选择题

1. 已知一次函数 $y = m n x$ 与 $y = m x + n$ （ $m$ ， $n$ 为常数，且 $m n \neq 0$ ），则它们在同一平面直角坐标系内的图象可能为（）

A、 B、 C、 D、

查看试题解析
2. 一条直线y=kx+b，其中k+b= $- 2022$ ， kb= $2021$ ，那么该直线经过（）

A、第二、四象限 B、第一、二、三象限 C、第一、三象限 D、第二、三、四象限

查看试题解析
3. 关于函数 $y = - 2 x - 1$ ，下列结论正确的是（）

A、图象必经过点 $(- 2 ， 1)$ B、y随x的增大而增大 C、当 $x > \frac{1}{2}$ 时， $y < 0$ D、图象经过第一、二、三象限

查看试题解析
4. 在学习了用描点法画函数图象之后，小马同学对某个一次函数列表取对应值如下：
x
…
-2
-1
0
1
2
…
y
…
-5
-3
-1
0
3
…
他在最后描点连线时发现有一个点明显不对，这个点是（）．

A、 $(- 1 ， - 3)$ B、 $(0 ， - 1)$ C、 $(1 ， 0)$ D、 $(2 ， 3)$

查看试题解析
5. 关于函数 $y = k x + k - 2$ ，给出下列说法正确的是：（）
①当 $k \neq 0$ 时，该函数是一次函数；
②若点 $A (m - 1 ， y_{1}) ， B (m + 3 ， y_{2})$ 在该函数图象上，且 $y_{1} < y_{2}$ ，则 $k > 0$ ；
③若该函数不经过第四象限，则 $k > 2$ ；
④该函数恒过定点 $(- 1 ， - 2)$ ．

A、①②④ B、①③④ C、②③④ D、①②③

查看试题解析
6. 如图，在平面直角坐标系中有一个 $3 \times 3$ 的正方形网格，其右下角格点（小正方形的顶点） $A$ 的坐标为 $(- 1 ， 1)$ ，左上角格点 $B$ 的坐标为 $(- 4 ， 4)$ ，若分布在直线 $y = - k x - k$ 两侧的格点数相同，则 $k$ 的取值可以是（）.

A、 $\frac{5}{2}$ B、 $\frac{7}{4}$ C、2 D、 $\frac{3}{2}$

查看试题解析
7. 一次函数 $y_{1} = k x + b$ 与 $y_{2} = m x + n$ 的图象如图所示，下列选项正确的是（）
①对于函数 $y_{1} = k x + b$ 来说， $s$ 随 $t$ 的增大而减小；
②函数 $y = k x + n$ 的图象不经过第一象限；
③ $2 k - 2 m = n - b$

A、①② B、①③ C、②③ D、①②③

查看试题解析
8. 已知过点 $（ 2 ， 3 ）$ 的直线 $y = a x + b （ a \neq 0 ）$ 不经过第四象限．设 $S = a + 2 b$ ，则（）

A、 $S$ 有最大值 $\frac{3}{2}$ B、 $S$ 有最小值 $\frac{3}{2}$ C、 $S$ 有最大值 $6$ D、 $S$ 有最小值 $6$

查看试题解析

二、填空题

9. 若点 $A (2 ， a + 1)$ ，点 $B (4 ， a)$ 是一次函数 $y = k x + 1$ 图象上的两点，则 $k$ 的值为．

查看试题解析
10. 在平面直角坐标系中，已知点 $A (1 ， 4)$ ，点 $B (3 ， 1)$ ，点 $M$ 的坐标为 $(- 1 ， m)$ ，当 $M A + M B$ 的值最小时 $m$ 的值为.

查看试题解析
11. 关于x的函数y＝（m+1）x﹣（4m﹣3）的图象在第一、二、四象限，那么m的取值范围是.

查看试题解析
12. 一次函数 $y = (k^{2} + 1) x - 2$ 的函数值 $y$ 随自变量 $x$ 的增大而（填“增大”或“减小”）

查看试题解析
13.
如图，点M是直线y=2x+3上的动点，过点M作MN垂直于x轴于点N，y轴上是否存在点P，使△MNP为等腰直角三角形，请写出符合条件的点P的坐标．

查看试题解析

三、解答题

14. 已知 $y$ 关于 $x$ 的一次函数 $y = k x + b (k \neq 0)$ ．当 $x = 4$ 时， $y = 6$ ；当 $x = 2$ 时， $y = 2$ ．

(1)、求 $k, b$ 的值；

(2)、若 $A (m, y_{1}), B (m + 1, y_{2})$ 是该函数图象上的两点，求证： $y_{2} - y_{1} = k$ ．

查看试题解析
15. 已知 $y$ 是关于 $x$ 的一次函数，如表列出了这个函数部分的对应值：
$x$
$- 3$
1
2
$n$
$y$
0
$m$
$- 1$
$- 4$

(1)、求这个一次函数的表达式．

(2)、求 $m$ ， $n$ 的值．

(3)、已知点 $A (x_{1}$ ， $y_{1})$ 和点 $B (x_{2}$ ， $y_{2})$ 在该一次函数图象上，设 $t = \frac{y_{1} - y_{2}}{x_{1} - x_{2}}$ ，判断正比例函数 $y = (t - 3) x$ 的图象是否有可能经过第一象限，并说明理由．

查看试题解析
16. 已知一次函数y＝（m+1）x+3﹣m ．

(1)、若该函数时一次函数，则m应满足什么条件；

(2)、在（1）的前提下，若其图像不经过第四象限，求m的取值范围；

(3)、在（1）的前提下，若点A（a ， b），B（a+1，c）在其图象上，求证：c-b-m=1

查看试题解析

17. 某公交车每天的支出费用为

600

元，每天的乘车人数

x (

人

)

与每天利润

(

利润

=

票款收入

-

支出费用

) y (

元

)

的变化关系如下表所示

(

每位乘客的乘车票价固定不变

)

：

$x ($ 人 $)$	$\dots$	$200$	$250$	$300$	$350$	$400$	$\dots$
$y ($ 元 $)$	$\dots$	$- 200$	$- 100$	$0$	$100$	$200$	$\dots$

(1)、观察表中数据可知，若要保证不亏本，该公交车每天乘客应达到多少人？

(2)、请你估计一天乘客人数为

500

人时，利润是多少？

(3)、写出

y

与

x

的关系表达式．

查看试题解析

18.
如图，直线l₁在平面直角坐标系中，直线l₁与y轴交于点A，点B（﹣3，3）也在直线l₁上，将点B先向右平移1个单位长度，再向下平移2个单位长度得到点C，点C恰好也在直线l₁上．
（1）求点C的坐标和直线l₁的解析式；
（2）若将点C先向左平移3个单位长度，再向上平移6个单位长度得到点D，请你判断点D是否在直线l₁上；
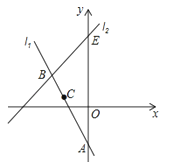
（3）已知直线l₂：y=x+b经过点B，与y轴交于点E，求△ABE的面积．

查看试题解析

x	…	-2	-1	0	1	2	…
y	…	-5	-3	-1	0	3	…

$x$	$- 3$	1	2	$n$
$y$	0	$m$	$- 1$	$- 4$

【提升版】北师大版数学八年级上册4.3一次函数的图象 同步练习

一、选择题

二、填空题

三、解答题

【提升版】北师大版数学八年级上册4.3一次函数的图象同步练习