中考数学复习-几何综合复习卷
试卷更新日期:2024-09-22 类型:复习试卷
一、单选题(每题3分,共30分)
-
1. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、一组对边平行,另一组对边相等的四边形是平行四边形 C、对角线互相垂直平分的四边形是菱形 D、一组邻边相等,并且有一个内角为直角的四边形是正方形2. 如图,点 在直线 上, ,那么下列说法错误的是( )
 A、 与 相等 B、 与 互余 C、 与 互补 D、 与 互余3. 如图,AB∥CD , ∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD= ( )
A、 与 相等 B、 与 互余 C、 与 互补 D、 与 互余3. 如图,AB∥CD , ∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD= ( ) A、110° B、115° C、125° D、130°4. 如图:有两条平行小路 ,这两条小路分别与一条公路 在 两处相交,并且相交的角度 ,现在想经过 处修一条水渠,使水渠与公路平行,那 的度数应该是( )
A、110° B、115° C、125° D、130°4. 如图:有两条平行小路 ,这两条小路分别与一条公路 在 两处相交,并且相交的角度 ,现在想经过 处修一条水渠,使水渠与公路平行,那 的度数应该是( ) A、120° B、30° C、60° D、80°5. 将一副三角板ABC如图放置,使点A在DE上,BC//DE,其中,则∠E=30°,则∠AFC的度数是( )
A、120° B、30° C、60° D、80°5. 将一副三角板ABC如图放置,使点A在DE上,BC//DE,其中,则∠E=30°,则∠AFC的度数是( ) A、45° B、50° C、60° D、75°6. 下列命题中假命题是( )A、任意两个等腰直角三角形都相似 B、任意两个含36°内角的等腰三角形相似 C、任意两个等边三角形都相似 D、任意两个直角边之比为1:2的直角三角形相似7. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1 , 第二次将点A向右移动6个单位长度到达点A2 , 第三次将点A2向左移动9个单位长度到达点A3 , 按照这种移动规律移动下去,第n次移动到点An , 如果点An与原点的距离不小于20,那么n的最小值是( )
A、45° B、50° C、60° D、75°6. 下列命题中假命题是( )A、任意两个等腰直角三角形都相似 B、任意两个含36°内角的等腰三角形相似 C、任意两个等边三角形都相似 D、任意两个直角边之比为1:2的直角三角形相似7. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1 , 第二次将点A向右移动6个单位长度到达点A2 , 第三次将点A2向左移动9个单位长度到达点A3 , 按照这种移动规律移动下去,第n次移动到点An , 如果点An与原点的距离不小于20,那么n的最小值是( )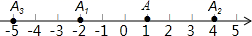 A、12 B、13 C、14 D、15
A、12 B、13 C、14 D、15二、填空题(每题3分,共18分)
-
8. 若∠α=30.2°,则∠α的补角度数为(用“°、'”表示).9. 在数轴上,与表示数-2的点距离是3的点所表示的数是.10. 如图,将周长为10的 沿 边向右平移4个单位,得到 则四边形 的周长为 .
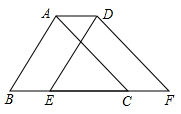 11. 如图,已知 , 、 为 上的两点, 、 为 上的两点,延长 于点 , 平分 ,点 在直线 上,且 平分 ,若 .则下列结论:① ;② ;③ ;④设 , ;⑤ 的度数为50°.其中正确结论为 . (填序号)
11. 如图,已知 , 、 为 上的两点, 、 为 上的两点,延长 于点 , 平分 ,点 在直线 上,且 平分 ,若 .则下列结论:① ;② ;③ ;④设 , ;⑤ 的度数为50°.其中正确结论为 . (填序号)
三、作图题(共2题,共16分)
-
12. 在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.已知三角形ABC的三个顶点都在格点上.(1)、按下列要求画图:过点B和一格点D画AC的平行线BD,过点C和一格点E画BC的垂线CE,并在图中标出格点D和E;(2)、求三角形ABC的面积.
 13. 如图,已知四点A、B、C、 , 请用尺规作图完成.(保留画图痕迹)
13. 如图,已知四点A、B、C、 , 请用尺规作图完成.(保留画图痕迹) (1)、画直线;(2)、画射线;(3)、连接;(4)、在线段上取点 , 使的值最小,你的依据是_▲_.
(1)、画直线;(2)、画射线;(3)、连接;(4)、在线段上取点 , 使的值最小,你的依据是_▲_.四、解答题(共7题,共62分)
-
14. 如图,如果AB//CD,平分交于点 , 交的延长线于点 , .试说明:AD//BC.
 15. 如图,已知 , , 平分 , 平分 . 求的度数.
15. 如图,已知 , , 平分 , 平分 . 求的度数.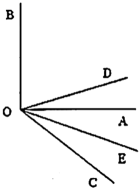
五、实践探究题(共2题,共24分)
-
16. 如图(a)所示,将一把含30°角的直角三角板ABC的BC边放置于长方形直尺DEFG的边上.
 (1)、填空:°,°.(2)、如图(b)所示,现把三角板绕点B逆时针旋转n°,当 , 且点C恰好落在DG边上时,① ▲ °, ▲ °;(结果用含n的代数式表示)
(1)、填空:°,°.(2)、如图(b)所示,现把三角板绕点B逆时针旋转n°,当 , 且点C恰好落在DG边上时,① ▲ °, ▲ °;(结果用含n的代数式表示)②若恰好是的倍,求n的值.
(3)、如图(a)所示放置的三角板ABC , 现将射线BF绕点B以2°/s的速度逆时针旋转得到射线BM , 同时射线QA绕点Q以3°/s的速度顺时针旋转得到射线QN , 当射线QN旋转至与QB重合时,则射线BM , QN均停止转动,设旋转时间为ts.①在旋转过程中,若射线BM与射线QN相交,设交点为P . 当时,则 ▲ .
②在旋转过程中,是否存在?若存在,求出此时t的值;若不存在,请说明理由.
17. (1)、问题情境:
(1)、问题情境:如图1,已知 AB∥CD,∠APC=108°.求∠PAB+∠PCD的度数.
经过思考,小敏提出思路:如图2,过点 P 作PE∥AB,根据平行线的有关性质,可得∠PAB+∠PCD= °.
(2)、问题迁移:如图3,AD∥BC,点 P 在射线OM 上运动,∠ADP=α,∠BCP=β.
当点 P 在A,B两点之间运动时,∠CPD,α,β之间有何数量关系? 请说明理由.
(3)、当点 P 在A,B 两点外侧运动时(点 P 与点A,B,O不重合),请直接写出∠CPD,α,β之间的数量关系.(4)、问题拓展:如图4, -An是一条折线段.
依据此图信息,把你所发现的结论用数学式子表达出来: