苏科版数学八年级上册第三章测试卷

试卷更新日期：2024-09-21 类型：单元试卷

进入出卷网下载

一、选择题

1. 一根旗杆在离地面3米处断裂，旗杆顶部落在离旗杆底部4米处，旗杆折断之前的高度是（）

A、5米 B、7米 C、8米 D、9米

查看试题解析
2. 如图，是一张直角三角形的纸片，两直角边 $A C = 6, B C = 8$ ，现将 $△ A B C$ 折叠，使点B点A重合，折痕为DE，则BD的长为（）

A、7 B、 $\frac{25}{4}$ C、6 D、 $\frac{11}{2}$

查看试题解析
3. 在Rt△ABC中，∠C＝90°，a＝12，b＝16，则c的长为（）

A、26 B、18 C、20 D、21

查看试题解析
4. 下列几组数中，不能作为直角三角形三边的是（）

A、1， $\sqrt{2}$ ， $\sqrt{3}$ B、7，24，25 C、4，5，6 D、 $\frac{3}{5}$ ， $\frac{4}{5}$ ，1

查看试题解析
5. 如图，有两棵树分别用线段AB和CD表示，树高AB＝15米，CD＝7米，两树间的距离BD＝6米，一只鸟从一棵树的树梢（点A）飞到另一棵树的树梢（点C），则这只鸟飞行的最短距离AC＝（）

A、6米 B、8米 C、10米 D、12米

查看试题解析
6. 如图，在锐角△ABC中，∠ACB＝50°；边AB上有一定点P，M、N分别是AC和BC边上的动点，当△PMN的周长最小时，∠MPN的度数是（）

A、50° B、60° C、70° D、80°

查看试题解析
7. 如图，等腰直角△ABC中，AC=BC ， BE平分∠ABC ， AD⊥BE的延长线于点D ，若AD=2，则△ABE的面积为（）．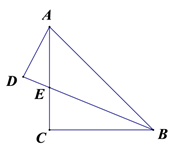

A、4 B、6 C、2 $\sqrt{3}$ D、2 $\sqrt{5}$

查看试题解析
8. 如图，在 $△ A B C$ 中， $A B = A C$ ， AD，CE是 $△ A B C$ 的两条中线，P是AD上的一个动点，则下列线段的长等于 $B P + E P$ 最小值的是（）

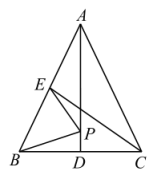A、AC B、BC C、AD D、CE

查看试题解析

二、填空题

9. 直角三角形两直角边长分别为5和12，则它斜边上的高为．

查看试题解析
10. 如图， $△ A B C$ 中， $A B = A C$ ， $B C = 5$ ， $S_{△ A B C} = 15$ ， $A D ⊥ B C$ 于点D， $E F$ 垂直平分 $A B$ ，交 $A C$ 于点F，在 $E F$ 上确定一点P，使 $P B + P D$ 最小，则这个最小值为．

查看试题解析
11. 如图甲是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，在 $R t △ A B C$ 中，若直角边 $A C = 6$ ， $B C = 5$ ，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图乙所示的“数学风车”，则这个风车的外围周长（图乙中的实线）是．

查看试题解析
12. 如图，有两棵树，一棵高12米，另一棵高7米，两树相距12米，一只小鸟从一棵树的树梢 $A$ 飞到另一棵树的树梢 $B$ ，则小鸟至少要飞行米．

查看试题解析
13. 如图，将一根长12厘米的筷子置于底面直径为6厘米，高为8厘米的圆柱形杯子中，则筷子露在杯子外面的长度至少为厘米.

查看试题解析
14. 如图，Rt△ABC的面积为20cm² ，在AB的同侧，分别以AB，BC，AC为直径作三个半圆，则阴影部分的面积为.

查看试题解析
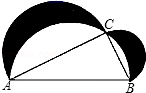15. 在△ABC中，∠C=90°，AB=5，则AB²+AC²+BC²= ．

查看试题解析

三、解答题

16. 如图，折叠矩形的一边 $A D$ ，使点 $D$ 落在 $B C$ 边的点 $F$ 处，已知AB=8cm，BC=10cm，求 $E C$ 的长

查看试题解析
17. 如图，学校有一块三角形空地ABC，计划将这块三角形空地分割成四边形ABDE和△EDC，分别摆放“秋海棠”和“天竺葵”两种不同的花卉，经测量，∠EDC=90°，DC=3，CE=5，BD=7，AB=8，AE=1，求四边形ABDE的面积．

查看试题解析
18. 阅读下列解题过程：
已知a、b、c为 $△ A B C$ 的三边长，且满足 $a^{2} c^{2} - b^{2} c^{2} = a^{4} - b^{4}$ ，试判断 $△ A B C$ 的形状.
解：因为 $a^{2} c^{2} - b^{2} c^{2} = a^{4} - b^{4}$ ，         ①
所以 $c^{2} (a^{2} - b^{2}) = (a^{2} - b^{2}) (a^{2} + b^{2})$ .        ②
所以 $c^{2} = a^{2} + b^{2}$ .                ③
所以 $△ A B C$ 是直角三角形.        ④
回答下列问题：

(1)、上述解题过程，从哪一步开始出现错误？该步的序号为；

(2)、错误的原因为；

(3)、请你将正确的解答过程写下来.

查看试题解析

四、综合题

19. 如图，一个梯子 $A B$ 长25米，顶端 $A$ 靠在墙 $A C$ 上（墙与地面垂直），这时梯子下端 $B$ 与墙角 $C$ 距离为7米．

(1)、求梯子顶端 $A$ 与地面的距离 $A C$ 的长；

(2)、若梯子的顶端 $A$ 下滑到 $E$ ，使 $A E = 4$ ，求梯子的下端 $B$ 滑动的距离 $B D$ 的长．

查看试题解析
20. 如图，已知△ABC中，∠B=90°，AB=8cm，BC=6cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．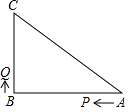

(1)、当t=2秒时，求PQ的长；

(2)、求出发时间为几秒时，△PQB是等腰三角形？

(3)、若Q沿B→C→A方向运动，则当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．

查看试题解析
21. 台风是一种自然灾害，它以台风中心为圆心在周围上百千米的范围内形成极端气候，有极强的破坏力，如图，有一台风中心沿东西方向 $A B$ 由 $A$ 行驶向 $B$ ，已知点 $C$ 为一海港，且点 $C$ 与直线 $A B$ 上的两点 $A$ ， $B$ 的距离分别为 $A C = 300 k m$ ， $B C = 400 k m$ ，又 $A B = 500 k m$ ，以台风中心为圆心周围 $250 k m$ 以内为受影响区域．

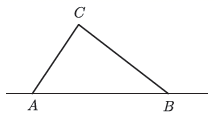(1)、求 $∠ A C B$ 的度数．

(2)、海港 $C$ 受台风影响吗？为什么？

(3)、若台风的速度为20千米/小时，当台风运动到点 $E$ 处时，海港 $C$ 刚好受到影响，当台风运动到点 $F$ 时，海港 $C$ 刚好不受影响，即 $C E = C F = 250 k m$ ，则台风影响该海港持续的时间有多长？

查看试题解析
22. 在四边形 $A B C D$ 中， $Δ O A B$ 和 $Δ O C D$ 有公共顶点O，且 $Δ O A B ≌ Δ O C D$ .

(1)、如图1，O是边 $B C$ 上的一点.若 $A D ∥ B C$ .求证： $A O = D O$ .

(2)、如图1，O是边 $B C$ 上的一点.若 $∠ A O D = 80 °$ ，连接 $A C ， B D$ ，交点为E，求 $∠ D E C$ 的度数.

(3)、如图2，B、O、C三点不在一条线上，且 $∠ A O B = 90 °$ ，满足 $A D^{2} + B C^{2} = 50 ， A O = 3$ ，求 $Δ O A B$ 的面积.

查看试题解析
23. 在 $Δ A B C$ 中， $A B = A C$ ， $D$ 是射线 $B C$ 上的一点，过点 $D$ 分别作 $D E ⊥ A B$ 于点 $E$ ， $D F ⊥ A C$ 于点 $F$ ．

(1)、如图1，若 $D$ 是 $B C$ 边上的中点，求证： $D E = D F$ ．

(2)、过点 $B$ 作 $B G ⊥ A C$ 于点 $G$ ．
①如图2，若 $D$ 是 $B C$ 边上的任意一点，求证： $B G = D E + D F$ ；

②若点 $D$ 是射线 $B C$ 上一点， $A B = 5$ ， $B C = 6$ ， $D F = 2$ ，求 $D E$ 的长度．

查看试题解析