苏科版数学八年级上册第二章测试卷
试卷更新日期:2024-09-21 类型:单元试卷
一、选择题
-
1. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性,下列汉字是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,屋顶钢架外框是等腰三角形,其中 , 工人师傅在焊接立柱时,只用找到的中点 , 这就可以说明竖梁垂直于横梁了,工人师傅这种操作方法的依据是( )
2. 如图,屋顶钢架外框是等腰三角形,其中 , 工人师傅在焊接立柱时,只用找到的中点 , 这就可以说明竖梁垂直于横梁了,工人师傅这种操作方法的依据是( )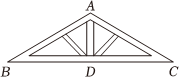 A、等边对等角 B、等角对等边
A、等边对等角 B、等角对等边
C、垂线段最短 D、等腰三角形“三线合一”3. 三条公路将A、B、C三个村庄连成一个如图的三角形区域,如果在这个区域内修建一个公园,要使公园到三个村庄的距离相等,那么这个公园应建的位置是的( ) A、三条高线的交点 B、三边垂直平分线的交点 C、三条角平分线的交点 D、三条中线的交点4. 如图,在中, , 点D是BC上一点,BD的垂直平分线交AB于点E,将沿AD折叠,点C恰好与点E重合,则等于( )
A、三条高线的交点 B、三边垂直平分线的交点 C、三条角平分线的交点 D、三条中线的交点4. 如图,在中, , 点D是BC上一点,BD的垂直平分线交AB于点E,将沿AD折叠,点C恰好与点E重合,则等于( )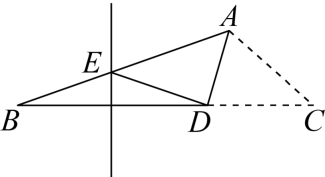 A、19° B、20° C、24° D、25°5. 如图, 是等边三角形, ,则 的度数为( )
A、19° B、20° C、24° D、25°5. 如图, 是等边三角形, ,则 的度数为( ) A、50° B、55° C、60° D、65°6. 如图所示,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:
A、50° B、55° C、60° D、65°6. 如图所示,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③DM平分∠EDF;④AB+AC=2AE.
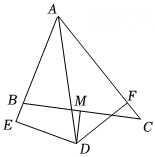
其中正确的有( )
A、1个 B、2个 C、3个 D、4个7. 如图,过边长为的等边三角形的边上一点 , 作于点为延长线上一点,当时,交于 , 则的长为( ) A、 B、 C、 D、不能确定8. 如图,在中,的垂直平分线与的外角平分线交于点D , 于点E , 交的延长线于点F , 则下列结论:①;②;③;④若 , , 则 , 其中一定成立的有( )
A、 B、 C、 D、不能确定8. 如图,在中,的垂直平分线与的外角平分线交于点D , 于点E , 交的延长线于点F , 则下列结论:①;②;③;④若 , , 则 , 其中一定成立的有( )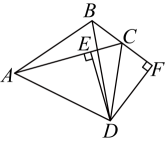 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 如图中, , 平分 , , , 则的面积是.
 10. 如图,在△ABC中,BI,CI分别平分∠ABC,∠ACF,直线DE过点I,且DE∥BC,BD=8 cm,CE=5 cm,则DE= .
10. 如图,在△ABC中,BI,CI分别平分∠ABC,∠ACF,直线DE过点I,且DE∥BC,BD=8 cm,CE=5 cm,则DE= . 11. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是.
11. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是. 12. 小明将两把完全相同的长方形直尺如图放置在上,两把直尺的接触点为P , 边与其中一把直尺边缘的交点为C , 点C、P在这把直尺上的刻度读数分别是2、5,则的长度是 .
12. 小明将两把完全相同的长方形直尺如图放置在上,两把直尺的接触点为P , 边与其中一把直尺边缘的交点为C , 点C、P在这把直尺上的刻度读数分别是2、5,则的长度是 . 13. 已知等腰三角形的一边长为4,另一边长为8,则这个等腰三角形的周长为 .14. 等腰三角形有一个角是36°,则它的顶角度数是 .15. 如图,△ABC中,AB=BC,∠ABC=120°,E是线段AC上一点,连接BE并延长至D,连接CD,若∠BCD=120°,AB=2CD,AE=9,则线段CE长为 .
13. 已知等腰三角形的一边长为4,另一边长为8,则这个等腰三角形的周长为 .14. 等腰三角形有一个角是36°,则它的顶角度数是 .15. 如图,△ABC中,AB=BC,∠ABC=120°,E是线段AC上一点,连接BE并延长至D,连接CD,若∠BCD=120°,AB=2CD,AE=9,则线段CE长为 . 16. 如图,在中, , , 的垂直平分线交于点 , 交于点 , 在直线上存在一点 , 使、、三点构成的的周长最小,则的周长最小值为 .
16. 如图,在中, , , 的垂直平分线交于点 , 交于点 , 在直线上存在一点 , 使、、三点构成的的周长最小,则的周长最小值为 . 17. 如图所示,在等腰中,为的中点,点在上, , 若点是等腰的腰上的一点,则当为等腰三角形时,的度数是.
17. 如图所示,在等腰中,为的中点,点在上, , 若点是等腰的腰上的一点,则当为等腰三角形时,的度数是. 18. 如图,过边长为2的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连接PQ交AC边于D,则下面结论:①PE=2AE;②D为PQ的中点;③CQ=2AE;④CQ+2CD=2;其中正确的结论有: .
18. 如图,过边长为2的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连接PQ交AC边于D,则下面结论:①PE=2AE;②D为PQ的中点;③CQ=2AE;④CQ+2CD=2;其中正确的结论有: .
三、作图题
-
19. 如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点)和直线l.
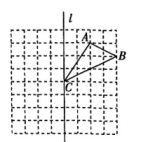 (1)、在直线l上找一点P,使点P到边AB,BC的距离相等;(2)、画出△ABC关于直线l对称的图形△A1B1C1;再将△A1B1C1向下平移4个单位长度,画出平移后得到的图形△A2B2C2;(3)、结合轴对称变换和平移变换的有关性质,两个对应图形△ABC和△A2B2C2的对应点所具有的性质是
(1)、在直线l上找一点P,使点P到边AB,BC的距离相等;(2)、画出△ABC关于直线l对称的图形△A1B1C1;再将△A1B1C1向下平移4个单位长度,画出平移后得到的图形△A2B2C2;(3)、结合轴对称变换和平移变换的有关性质,两个对应图形△ABC和△A2B2C2的对应点所具有的性质是(A)对应点连线互相平行.
(B)对应点连线被直线l垂直平分.
(C)对应点连线被直线l平分或与直线l重合.
四、解答题
-
20. 如图,为任意三角形,以边、为边分别向外作等边三角形和等边三角形 , 连接、并且相交于点 .
 (1)、求证:;(2)、 .21. 如图,在△ABC中,是的中点, , , 垂足分别是、 , 且 .
(1)、求证:;(2)、 .21. 如图,在△ABC中,是的中点, , , 垂足分别是、 , 且 .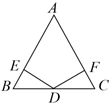 (1)、求证: .(2)、连接AD,求证:AD⊥BC.22. 如图,在△ABC中,AB=AC, BC=6,AM平分∠BAC,D为AC的中点,且DM= AC,E为BC延长线上一点,且CE= BC.
(1)、求证: .(2)、连接AD,求证:AD⊥BC.22. 如图,在△ABC中,AB=AC, BC=6,AM平分∠BAC,D为AC的中点,且DM= AC,E为BC延长线上一点,且CE= BC.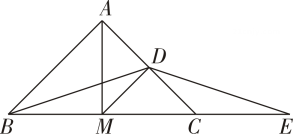 (1)、求ME的长;(2)、求证:△DBE是等腰三角形。23. 如图,中, , , 于 , 平分分别与 , 交于点 , .
(1)、求ME的长;(2)、求证:△DBE是等腰三角形。23. 如图,中, , , 于 , 平分分别与 , 交于点 , . (1)、求证:是等边三角形;(2)、若 , 求的长24. 在等边△ABC中,点D是边BC上一点.作射线AD , 点B关于射线AD的对称点为点E . 连接CE并延长,交射线AD于点F .
(1)、求证:是等边三角形;(2)、若 , 求的长24. 在等边△ABC中,点D是边BC上一点.作射线AD , 点B关于射线AD的对称点为点E . 连接CE并延长,交射线AD于点F .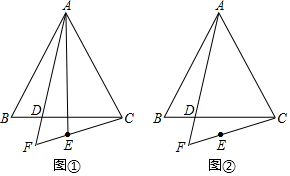 (1)、如图①,连接AE ,
(1)、如图①,连接AE ,①AE与AC的数量关系是 ▲ ;
②设∠BAF=a , 用a表示∠BCF的大小;
(2)、如图②,用等式表示线段AF , CF , EF之间的数量关系,并证明.
-

