苏科版数学八年级上册第一章测试卷
试卷更新日期:2024-09-19 类型:单元试卷
一、选择题(每题2分,共16分)
-
1. 下列命题中是真命题的是( )A、相等的角是对顶角 B、同旁内角相等,两直线平行 C、全等三角形的对应边相等 D、如果 , 那么2. 如图,小敏做了一个角平分仪 , 其中 , , 将仪器上的点A与的顶点R重合,调整和 , 使它们分别落在角的两边上,过点A、C画一条射线 , 就是的平分线.此角平分仪的画图原理是( )
 A、 B、 C、 D、3. 如图,是的角平分线, , 垂足为 , //交的延长线于点 , 若恰好平分 , . 给出下列四个结论:①;②//;③;④ . 其中正确的结论共有( )
A、 B、 C、 D、3. 如图,是的角平分线, , 垂足为 , //交的延长线于点 , 若恰好平分 , . 给出下列四个结论:①;②//;③;④ . 其中正确的结论共有( ) A、4个 B、3个 C、2个 D、1个4. 如图,在△ABC中,AB=AC,BE、CF是中线,则由( )可得△AFC≌△AEB.
A、4个 B、3个 C、2个 D、1个4. 如图,在△ABC中,AB=AC,BE、CF是中线,则由( )可得△AFC≌△AEB. A、SSS B、SAS C、AAS D、ASA5. 如图,已知平分 , 于 , , 则下列结论:①;②;③;④;其中正确结论的个数是( )
A、SSS B、SAS C、AAS D、ASA5. 如图,已知平分 , 于 , , 则下列结论:①;②;③;④;其中正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个6. 如图,在三边都不相等的中, , 垂足为M, , 垂足为N,且 , Q在AC上, , 下列结论:①;②;③;④ . 其中正确的有( )
A、1个 B、2个 C、3个 D、4个6. 如图,在三边都不相等的中, , 垂足为M, , 垂足为N,且 , Q在AC上, , 下列结论:①;②;③;④ . 其中正确的有( ) A、1个 B、2个 C、3个 D、4个7. 如图,已知中, , , 是高和的交点,则线段的长度为( )
A、1个 B、2个 C、3个 D、4个7. 如图,已知中, , , 是高和的交点,则线段的长度为( ) A、2 B、4 C、5 D、不能确定
A、2 B、4 C、5 D、不能确定二、填空题(每题2分,共16分)
-
8. 如图,在中, , D,E分别是 , 上的点.若 , 则 .
 9. 如图,点B、E、C、F在一条直线上,AB∥DE,且AB=DE,请添加一个条件 , 使△ABC≌△DEF.
9. 如图,点B、E、C、F在一条直线上,AB∥DE,且AB=DE,请添加一个条件 , 使△ABC≌△DEF. 10. 如图, , 点A,D,B,C分别在直线MN与PQ上,点在AB上, , , 则.
10. 如图, , 点A,D,B,C分别在直线MN与PQ上,点在AB上, , , 则. 11. 如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接并延长到D,使;连接并延长到E,使 , 由和全等得到 . 那么判定其全等的依据是(用三个字母表示).
11. 如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接并延长到D,使;连接并延长到E,使 , 由和全等得到 . 那么判定其全等的依据是(用三个字母表示). 12. 如图,在 △ABC 中,BE平分 ∠ABC , AE⊥BE 于点E, △BCE 的面积为2,则 △ABC 的面积是.
12. 如图,在 △ABC 中,BE平分 ∠ABC , AE⊥BE 于点E, △BCE 的面积为2,则 △ABC 的面积是. 13. 如图,在Rt△ABC中,∠BAC=90°,AB=AC , 点D为BC上一点,连接AD . 过点B作BE⊥AD于点E , 过点C作CF⊥AD交AD的延长线于点F . 若BE=4,CF=1,则EF的长度为 .
13. 如图,在Rt△ABC中,∠BAC=90°,AB=AC , 点D为BC上一点,连接AD . 过点B作BE⊥AD于点E , 过点C作CF⊥AD交AD的延长线于点F . 若BE=4,CF=1,则EF的长度为 .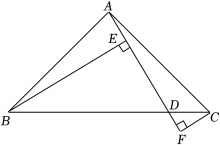 14. 如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF= .
14. 如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF= .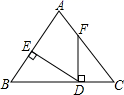 15. 如图,在△ABC中,AB=AC , AD平分∠BAC , DE⊥AB于点E , BF⊥AC于点F , DE=1.3cm , 则BF=cm .
15. 如图,在△ABC中,AB=AC , AD平分∠BAC , DE⊥AB于点E , BF⊥AC于点F , DE=1.3cm , 则BF=cm .
三、作图题(8分)
-
16. 如图,在中, .
 (1)、尺规作图,在上求作一点 , 使不要求写作法,保留作图痕迹;请你根据所学的三角形全等的有关知识,作图依据是 提示:、、、(2)、若(1)中 , , 求的度数.
(1)、尺规作图,在上求作一点 , 使不要求写作法,保留作图痕迹;请你根据所学的三角形全等的有关知识,作图依据是 提示:、、、(2)、若(1)中 , , 求的度数.四、解答题(共2题,共16分)
-
17. 已知:AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E,BD、CE相交于点F,
 (1)、如图1,求证:BE=CD.(2)、如图2,连接AF,在不添加任何辅助线的情况下,请直接写出图2中所有的全等三角形.18. 如图, , 垂足分别为 .
(1)、如图1,求证:BE=CD.(2)、如图2,连接AF,在不添加任何辅助线的情况下,请直接写出图2中所有的全等三角形.18. 如图, , 垂足分别为 . (1)、求证:;(2)、若 , 求四边形的面积.
(1)、求证:;(2)、若 , 求四边形的面积.五、综合题(共5题,共44分)
-
19. 如图,中, , , , , 的角平分线交于点G,作 ,
 (1)、求证:(2)、如图连接交于E.求证:(3)、若 , , 求的面积.20. 如图,在 中,按以下步骤作图:
(1)、求证:(2)、如图连接交于E.求证:(3)、若 , , 求的面积.20. 如图,在 中,按以下步骤作图:
①以点B为圆心,任意长为半径作弧,分别交BA,BC于点M,N;再以点N为圆心,MN长为半径作弧交前面的弧于点F,作射线BF交AC的延长线于点E.
②以点B为圆心,BA长为半径作弧交BE于点D,连接CD.请你观察图形,解答下列问题.
(1)、由尺规作图可证得 ,依据是;(2)、求证: ;(3)、若 , ,求∠ACB的度数.21. 如图,在中, , , 为边的中点,过点A作交的延长线于点平分交于点 , 为边上一点,连接 , 且 . 求证: (1)、 ;(2)、 .22. 在中, , , 过点C作直线 , 于点M,于点N.
(1)、 ;(2)、 .22. 在中, , , 过点C作直线 , 于点M,于点N.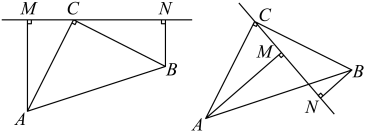 (1)、若在外(如图1),求证:;(2)、若与线段相交(如图2),且 , , 则 .23.
(1)、若在外(如图1),求证:;(2)、若与线段相交(如图2),且 , , 则 .23. (1)、如图1,在四边形ABCD中,AB=AD , ∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD , 线段EF、BE、FD之间的关系是;(不需要证明)(2)、如图2,在四边形ABCD中,AB=AD , ∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD , (1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.(3)、如图3,在四边形ABCD中,AB=AD , ∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD , (1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
(1)、如图1,在四边形ABCD中,AB=AD , ∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD , 线段EF、BE、FD之间的关系是;(不需要证明)(2)、如图2,在四边形ABCD中,AB=AD , ∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD , (1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.(3)、如图3,在四边形ABCD中,AB=AD , ∠B+∠D=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD , (1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.
-