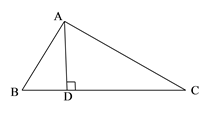苏科版数学八上第一章全等三角形单元测试卷
试卷更新日期:2024-09-19 类型:单元试卷
一、选择题
-
1. 如图,在中, , 平分交于点D , 平分交于点E , , 交于点F . 则下列说法正确的有( )
①;②;③若 , 则;④ .
A、1个 B、2个 C、3个 D、4个2. 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=S△ABP,其中正确的是( ) A、①③ B、①②④ C、①②③ D、②③3. 如图,在四边形中, , 若的平分线交于点 , 连接 , 且平分 , 则下列结论:①;②为的中点;③;④ , 其中正确的是( ).
A、①③ B、①②④ C、①②③ D、②③3. 如图,在四边形中, , 若的平分线交于点 , 连接 , 且平分 , 则下列结论:①;②为的中点;③;④ , 其中正确的是( ). A、①②③ B、①③④ C、②③④ D、①②③④4. 如图,已知是的平分线, , 若 , 则△ABC的面积等于( )
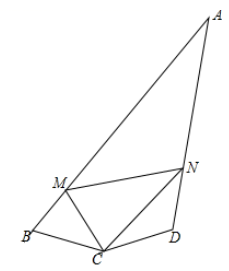
A、①②③ B、①③④ C、②③④ D、①②③④4. 如图,已知是的平分线, , 若 , 则△ABC的面积等于( ) A、 B、 C、 D、不能确定5. 如图,交于点M,交于点D,交于点N, , , , 给出下列结论:①;②;③;④ . 其中正确的结论有( )
A、 B、 C、 D、不能确定5. 如图,交于点M,交于点D,交于点N, , , , 给出下列结论:①;②;③;④ . 其中正确的结论有( ) A、4个 B、3个 C、2个 D、1个6. 如图,在△OAB和△OCD中,OA=OB , OC=OD , OA>OC , ∠AOB=∠COD=30°,如图,连接AC , BD交于点M , AC与OD相交于E , BD与OA相交于F , 连接OM . 则下列结论中:①AC=BD;②∠AMB=30°;③△OEM≌△OFM;④MO平分∠BMC . 正确的个数有( )
A、4个 B、3个 C、2个 D、1个6. 如图,在△OAB和△OCD中,OA=OB , OC=OD , OA>OC , ∠AOB=∠COD=30°,如图,连接AC , BD交于点M , AC与OD相交于E , BD与OA相交于F , 连接OM . 则下列结论中:①AC=BD;②∠AMB=30°;③△OEM≌△OFM;④MO平分∠BMC . 正确的个数有( ) A、1个 B、2个 C、3个 D、4个7. 已知AD是△ABC中BC边上的中线,AB=10,AC=6,则AD的取值范围是( )A、4<AD<16 B、2<AD<8 C、4<AD<10 D、8≤AD≤168. 如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当时间t为( )s时,能够使△BPE与△CQP全等.
A、1个 B、2个 C、3个 D、4个7. 已知AD是△ABC中BC边上的中线,AB=10,AC=6,则AD的取值范围是( )A、4<AD<16 B、2<AD<8 C、4<AD<10 D、8≤AD≤168. 如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当时间t为( )s时,能够使△BPE与△CQP全等. A、1 B、1或4 C、1或2 D、3
A、1 B、1或4 C、1或2 D、3二、填空题
-
9. 如图,在 中, 厘米, , 厘米,点 为 的中点.如果点 在线段 上以4厘米/秒的速度由 点向 点运动,同时,点 在线段 上由 点向 点运动.当点 的运动速度为厘米/秒时,能够在某一时刻使 与 全等.
 10. 如图,在中,是高, , , 在边上取点 , 连接 , , 若 , , 则 .
10. 如图,在中,是高, , , 在边上取点 , 连接 , , 若 , , 则 . 11. 三个全等三角形按如图的形式摆放,则的度数是.
11. 三个全等三角形按如图的形式摆放,则的度数是. 12. 如图,点O在直线m上,在m的同侧有A,B两点,∠AOB=90°,OA=10cm,OB=8cm,点P以2cm/s的速度从点A出发沿A—O—B路径向终点B运动,同时点Q以1cm/s的速度从点B出发沿B—O—A路径向终点A运动,两点都要到达相应的终点时才能停止运动,分别过点P,Q作PC⊥m于点 C,QD⊥m 于点C,QD⊥m于点D.若△OPC与△OQD全等,则点Q运动的时间是秒.
12. 如图,点O在直线m上,在m的同侧有A,B两点,∠AOB=90°,OA=10cm,OB=8cm,点P以2cm/s的速度从点A出发沿A—O—B路径向终点B运动,同时点Q以1cm/s的速度从点B出发沿B—O—A路径向终点A运动,两点都要到达相应的终点时才能停止运动,分别过点P,Q作PC⊥m于点 C,QD⊥m 于点C,QD⊥m于点D.若△OPC与△OQD全等,则点Q运动的时间是秒. 13. 如图,中, , , 是的角平分线, , 则的最大值为 .
13. 如图,中, , , 是的角平分线, , 则的最大值为 . 14. 如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形,画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画个.
14. 如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形,画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画个.
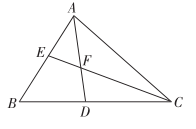
 15. 如图,△ABC中,AD、BD、CD分别平分△ABC的外角∠CAE、内角∠ABC、外角∠ACF,AD∥BC.以下结论:①∠ABC=∠ACB;②∠ADC+∠ABD=90°;③BD平分∠ADC;④2∠BDC=∠BAC.其中正确的结论有 . (填序号)
15. 如图,△ABC中,AD、BD、CD分别平分△ABC的外角∠CAE、内角∠ABC、外角∠ACF,AD∥BC.以下结论:①∠ABC=∠ACB;②∠ADC+∠ABD=90°;③BD平分∠ADC;④2∠BDC=∠BAC.其中正确的结论有 . (填序号)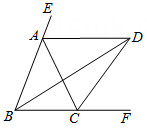 16. 如图,在△ABC中,BD、CE是△ABC的角平分线,BD,CE交于点O.过点O作OF⊥BC,垂足为F,若∠BAC=120°,OD•OE=12,BC−BE−CD=5,则OF=.
16. 如图,在△ABC中,BD、CE是△ABC的角平分线,BD,CE交于点O.过点O作OF⊥BC,垂足为F,若∠BAC=120°,OD•OE=12,BC−BE−CD=5,则OF=. 17. 如图,D为等腰Rt△ABC的斜边AB的中点,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G,交BC的延长线于H,则以下结论:①BE=CG;②DF=DH;③BH=CF;④AF=CH.其中正确的是.
17. 如图,D为等腰Rt△ABC的斜边AB的中点,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G,交BC的延长线于H,则以下结论:①BE=CG;②DF=DH;③BH=CF;④AF=CH.其中正确的是. 18. 如图, ,点 是边 上的点, 平分 , 平分 ,有下列结论:① ,② 为 的中点,③ ,④ ,其中正确的有.(填序号)
18. 如图, ,点 是边 上的点, 平分 , 平分 ,有下列结论:① ,② 为 的中点,③ ,④ ,其中正确的有.(填序号)
三、证明题
-
19. 如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,BE=DF,CE=CF.求证:AE=AF.
 20. 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一动点,延长BD交CE于E,且CE⊥BD,若BD平分∠ABC,求证:CE= BD
20. 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一动点,延长BD交CE于E,且CE⊥BD,若BD平分∠ABC,求证:CE= BD 21. 如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .
21. 如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .