新人教版七年级上学期数学第六章质量高阶检测
试卷更新日期:2024-09-13 类型:单元试卷
一、选择题(每题3分)
-
1. 两个角的和与这两个角的差互补,则这两个角( ).A、一个是锐角,一个是钝角 B、都是钝角 C、都是直角 D、必有一个是直角2. 下列四个正方体的展开图中,能折叠成如图所示的正方体的是( )
 A、
A、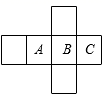 B、
B、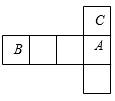 C、
C、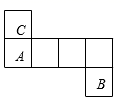 D、
D、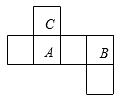 3. 如果线段AB=13cm,MA+MB=17 cm,那么下面说法中正确的是( ).A、M点在线段AB上 B、M点在直线AB上 C、M点在直线AB外 D、M点可能在直线AB上,也可能在直线AB外4. 如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
3. 如果线段AB=13cm,MA+MB=17 cm,那么下面说法中正确的是( ).A、M点在线段AB上 B、M点在直线AB上 C、M点在直线AB外 D、M点可能在直线AB上,也可能在直线AB外4. 如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( ) A、点A B、点B C、AB之间 D、BC之间5. 在数轴上,点M、N分别表示数m,n.则点M、N之间的距离为 .已知点A,B,C,D在数轴上分别表示的数为a,b,c,d.且 ,则线段的长度为( )A、4.5 B、1.5 C、6.5或1.5 D、4.5或1.56. 如图,点 为线段 外一点,点 , , , 为 上任意四点,连接 , , , ,下列结论错误的是( )
A、点A B、点B C、AB之间 D、BC之间5. 在数轴上,点M、N分别表示数m,n.则点M、N之间的距离为 .已知点A,B,C,D在数轴上分别表示的数为a,b,c,d.且 ,则线段的长度为( )A、4.5 B、1.5 C、6.5或1.5 D、4.5或1.56. 如图,点 为线段 外一点,点 , , , 为 上任意四点,连接 , , , ,下列结论错误的是( ) A、以 为顶点的角共有15个 B、若 , ,则 C、若 为 中点, 为 中点,则 D、若 平分 , 平分 , ,则7. 如图,AB=30,C为射线AB上一点,BC比AC的4倍少20,P、Q两点分别从AB两点同时出发分别以2单位/秒和l单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:①BC=2AC;②运动过程中,QM的长度保持不变;③AB=4NQ;④当BQ=PB时,t=12.其中正确结论的个数是( )
A、以 为顶点的角共有15个 B、若 , ,则 C、若 为 中点, 为 中点,则 D、若 平分 , 平分 , ,则7. 如图,AB=30,C为射线AB上一点,BC比AC的4倍少20,P、Q两点分别从AB两点同时出发分别以2单位/秒和l单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:①BC=2AC;②运动过程中,QM的长度保持不变;③AB=4NQ;④当BQ=PB时,t=12.其中正确结论的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(每题3分)
-
8. 如图,将一段长为100cm绳子AB拉直铺平后折叠(绳子无弹性,折叠处长度忽略不计),使绳子与自身一部分重叠.若将绳子AB沿N点折叠后,点B落在处(点始终在点A右侧),在重合部分上沿绳子垂直方向剪断,将绳子分为三段,若这三段的长度由短到长的比为2∶3∶5,BN的值可能为 .
 9. 已知 , , , 则锐角的度数 .10. 如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是 .
9. 已知 , , , 则锐角的度数 .10. 如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是 . 11. 如图,点在线段的延长线上,且线段 , 第一次操作:分别取线段和的中点 , ;第二次操作:分别取线段和的中点 , ;第三次操作:分别取线段和的中点 , ;连续这样操作次,则 .
11. 如图,点在线段的延长线上,且线段 , 第一次操作:分别取线段和的中点 , ;第二次操作:分别取线段和的中点 , ;第三次操作:分别取线段和的中点 , ;连续这样操作次,则 .
三、解答题
-
12. 如图1,一个边长为2cm的立方体按某种方式展开后,恰好能放在一个长方形内.
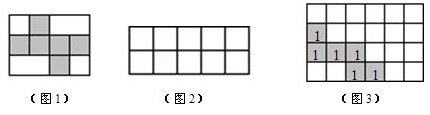 (1)、计算图1长方形的面积;(2)、小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);(3)、如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.13.
(1)、计算图1长方形的面积;(2)、小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);(3)、如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.13.如图①、②、③、④四个图形都是平面图形,观察图②和表中对应数值,探究计数的方法并解答下面的问题.
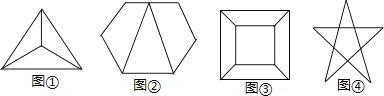
(1)数一数每个图各有多少顶点、多少条边、这些边围成多少区域,将结果填入下表:
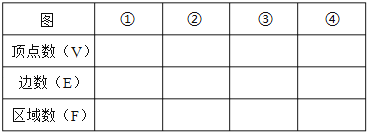
(2)根据表中的数值,写出平面图的顶点数、边数、区域数之间的关系;
(3)如果一个平面图形有20个顶点和11个区域,求这个平面图形的边数.
14. 下面是宿州市某集团校社团活动中一个数学兴趣小组研究的“数学实践活动”中三角尺中的数学问题. (1)、如图1,将两块直角三角尺的直角顶点C叠放在一起,.
(1)、如图1,将两块直角三角尺的直角顶点C叠放在一起,.①若 , 则 ▲ °;..
若 , 则 ▲ °;
②猜想与之间的数量关系,并说明理由;
(2)、如图2,若是两个同样的直角三角尺,将它们的锐角顶点A重合在一起, , 直接写出与之间的数量关系.15. 【问题情境】小圣所在的综合实践小组准备制作一些无盖纸盒收纳班级讲台上的粉笔.

【操作探究】
(1)、图1中的哪些图形经过折叠能围成无盖正方体纸盒?(填序号).(2)、小圣所在的综合实践小组把折叠成6个棱长都为的无盖正方体纸盒摆成如图2所示的几何体.①请计算出这个几何体的体积;
②如果在这个几何体上再添加一些相同的正方体纸盒,并保持从上面看到的形状和从左面看到的形状不变,最多可以再添加 个正方体纸盒.
16. 新定义:如果两个角的和为 , 我们称这两个角互为“兄弟角”.已知 , 与互为“兄弟角”,与互余. (1)、如图,当点在的内部,且点 , 点在的同侧时:
(1)、如图,当点在的内部,且点 , 点在的同侧时:①若 , 则______°.
②若 , 射线在内部,且满足 , 求的度数(用含的式子表示).
(2)、直接写出所有可能的度数:______(可用含的式子表示).17. 探究题:如图①,已知线段AB=14cm,点C为AB上的一个动点,点D、E分别是AC和BC的中点. (1)、若点C恰好是AB中点,则DE=cm;(2)、若AC=4cm,求DE的长;(3)、试利用“字母代替数”的方法,设AC=a cm请说明不论a取何值(a不超过14cm),DE的长不变;(4)、知识迁移:如图②,已知∠AOB=120°,过角的内部任一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE=60°与射线OC的位置无关.
(1)、若点C恰好是AB中点,则DE=cm;(2)、若AC=4cm,求DE的长;(3)、试利用“字母代替数”的方法,设AC=a cm请说明不论a取何值(a不超过14cm),DE的长不变;(4)、知识迁移:如图②,已知∠AOB=120°,过角的内部任一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE=60°与射线OC的位置无关.