【培优版】浙教版数学九上3.3 垂径定理 同步练习
试卷更新日期：2024-09-10 类型：同步测试
一、选择题
-
1. 如图，⊙O的直径CD垂直弦AB于点E，且CE=2，DE=8，则AB的长为（ ）
A、2 B、4 C、6 D、82. 如图，AB是的弦，AB的长为6，P是上一个动点(不与点A，B重合).过点O作AP于点 ， 作于点 ， 则CD的长为（ ）
A、1 B、2 C、3 D、43. 数学活动课上，同学们要测一个如图所示的残缺圆形工件的半径，小明的解决方案是：在工件圆弧上任取两点A ， B ， 连接AB ， 作AB的垂直平分线CD交AB于点D ， 交于点C ， 测出AB＝40cm ， CD＝10cm ， 则圆形工件的半径为（ ）
A、50cm B、35cm C、25cm D、20cm4. 如图，这是一种用于液体蒸馏或分馏物质的玻璃容器——蒸馏瓶，其底部是圆球形．球的半径为 ， 瓶内液体的最大深度 ， 则截面圆中弦的长为（ ）
A、 B、 C、 D、5. 如何只用一张矩形纸条和刻度尺测量出一次性纸杯杯口的直径?小聪同学想到了如下方法：如图所示，将纸条拉直紧贴杯口上，纸条的上下边沿分别与杯口相交于A，B，C，D四点，利用刻度尺量得该纸条宽为3.5cm，AB=3cm，CD=4cm，则纸杯的直径为（ ）
A、4cm B、5cm C、6cm D、7cm6. 我国明代科学家徐光启在《农政全书》中描绘了一种我国古代常用的水利灌溉工具——筒车，如图，筒车盛水桶的运行轨道是以轴心为圆心的圆，已知圆心在水面的上方，的半径长为5米，被水面截得的弦长为8米，点是运行轨道的最低点，则点到弦的距离为（ ）
A、5米 B、4米 C、3米 D、2米7. 如图，M为弦上的一点，连接过点M作交圆O于点C ． 若 ， 则的长为 （ ）
A、5 B、6 C、 D、8. 如图，AB为⊙O的直径，弦CD⊥AB于点F，OE⊥AC于点E，若OE＝3，OB＝5，则CD的长度是（ ）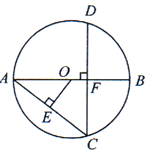
A、9.6 B、4 C、5 D、10二、填空题
-
9. 如图，在⊙O中，直径AB⊥CD于点E ， CD＝6，BE＝1，则弦AC的长为 ．
10. “青山绿水，畅享生活”，人们经常将圆柱形竹筒改造成生活用具，图1所示是一个竹筒水容器，图为该竹筒水容器的截面．已知截面的半径为 ， 开口宽为 ， 这个水容器所能装水的最大深度是 ．
11. 如图，以G（0，3）为圆心，半径为6的圆与x轴交于A ， B两点，与y轴交于C ， D两点，点E为⊙G上一动点，CF⊥AE于F ， 点E在G的运动过程中，线段FG的长度的最小值为 ．
12. 如图1是一款轴对称“磁悬浮地漏”无水时的示意图，它由一个圆弧形密封盖与两个磁体组成（下侧磁体固定不动），连接杆EF与地面BD垂直，排水口 ， 密封盖最高点E到地面的距离为6mm，整个地漏的高度EG＝75mm（G为磁体底部中点），密封盖被磁体顶起将排水口密封，所在圆的半径为 mm；当有水时如图2所示，密封盖下移排水，当密封盖下沉至最低处时，点M'恰好落在BG中点，若点M'到E'F'的距离为36mm，则密封盖下沉的最大距离为 mm．
三、解答题
-
13.(1)、如图，在中， ， 将绕点逆时针旋转得到 ， 求的度数；
(2)、下图是某学校人行过道中的一个以为圆心的圆形拱门，路面的宽为 ， 高为 ， 求圆形拱门所在圆的半径．
14. 如图①是从正面看到的一个面碗的形状示意图．是⊙O的一部分． D是AB的中点，连接OD，与弦AB交于C．连接OA、OB．已知AB=24cm．碗深CD=8cm，问⊙O的半径OA是多少？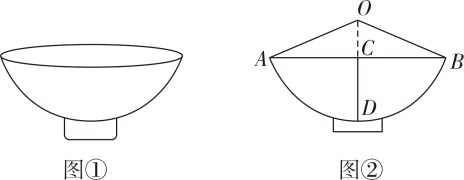
15. 如图，要把破残的圆片复制完整，已知弧上三点A、B、C.
(1)、用尺规作图法，找出弧BAC所在圆的圆心O；(保留作图痕迹，不写作法)(2)、设△ABC为等腰三角形，底边BC=10 cm，腰AB=6 cm，求圆片的半径R；(结果保留根号)(3)、若在(2)题中的R满足n＜R＜m(m、n为正整数)，试估算m和n的值.16. 如图，已知⊙O的弦AB垂直平分半径OC ， 连接AO并延长交⊙O于点E ， 连接DE ， 若AB＝4 ，请完成下列计算
(1)、求⊙O的半径长；(2)、求DE的长．四、实践探究题
-
17. 《九章算术》是中国传统数学重要的著作，奠定了中国传统数学的基本框架．《九章算术》中记载(如图①)：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，间径几何？”
阅读完这段文字后，聪聪画出了一个圆柱截面示意图(如图②)，其中BO⊥CD于点A，求“间径”就是要求⊙O的直径．根据上面记载的文字，发现AB= 寸，CD= 寸(一尺等于十寸)．运用有关知识即可解决这个问题．请你补全题目条件，并帮助聪聪求出⊙O的直径．
18. 根据背景素材，探索解决问题．测算石拱桥拱圈的半径
素材1
某数学兴趣小组测算一座石拱桥拱圈的半径（如图1），石拱桥由矩形的花岗岩叠砌而成，上、下的花岗岩错缝连接（花岗岩的各个顶点落在上、下花岗岩各边的中点，如图2所示）．
素材2
通过观察发现A，B，C三个点都在拱圈上，A是拱圈的最高点，且在两块花岗岩的连接处，B，C两个点都是花岗岩的顶点（如图3）．
素材3
如果没有带测量工具，那么可以用身体的“尺子”来测，比如前臂长（包括手掌、手指）（如图4），利用该方法测得一块花岗岩的长和宽（如图5）．
问题解决
任务1
获取数据
通过观察、计算B，C两点之间的水平距离及铅垂距离（高度差）．
任务2
分析计算
通过观察、计算石拱桥拱圈的半径．
注：测量、计算时，都以“肘”为单位．