【提升版】浙教版数学九上3.3 垂径定理 同步练习
试卷更新日期:2024-09-10 类型:同步测试
一、选择题
-
1. 如图,⊙O的直径 垂直于弦 ,垂足为 .若 , ,则 的长是( )
 A、4 B、 C、2 D、2. 《九章算术》是我国古代著名数学著作,书中记载:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图, 为 的直径,弦 于 , 寸, 寸,求直径 的长.”则 ( )
A、4 B、 C、2 D、2. 《九章算术》是我国古代著名数学著作,书中记载:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图, 为 的直径,弦 于 , 寸, 寸,求直径 的长.”则 ( ) A、 寸 B、 寸 C、 寸 D、 寸3. ⊙O的半径为5,M是圆外一点,MO=6,∠OMA=30°,则弦AB的长为( )
A、 寸 B、 寸 C、 寸 D、 寸3. ⊙O的半径为5,M是圆外一点,MO=6,∠OMA=30°,则弦AB的长为( )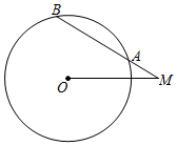 A、4 B、6 C、6 D、84. 半径等于4的圆中,垂直平分半径的弦长为( )A、 B、 C、 D、5. 如图,⊙O的弦CD交直径AB于E,OD=DE,CE:DE=3:5,若OE=5,则CD的长为( )
A、4 B、6 C、6 D、84. 半径等于4的圆中,垂直平分半径的弦长为( )A、 B、 C、 D、5. 如图,⊙O的弦CD交直径AB于E,OD=DE,CE:DE=3:5,若OE=5,则CD的长为( )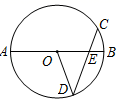 A、4 B、4 C、3 D、36. 如图,的半径为5,弦 , 点C在弦AB上,延长CO交于点D,则CD的取值范围是( )
A、4 B、4 C、3 D、36. 如图,的半径为5,弦 , 点C在弦AB上,延长CO交于点D,则CD的取值范围是( )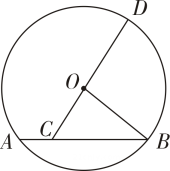 A、 B、 C、 D、7. 如图,的半径弦于点E , C是上一点, , 的最大值为18,则的长为( )
A、 B、 C、 D、7. 如图,的半径弦于点E , C是上一点, , 的最大值为18,则的长为( ) A、8 B、6 C、4 D、28. A、C是以半径为6的圆的圆周上的两点,为的中点,以线段BA,BC为邻边作菱形ABCD,顶点恰好为该圆直径的三等分点,则该菱形的边长为( )A、或 B、或 C、或 D、或
A、8 B、6 C、4 D、28. A、C是以半径为6的圆的圆周上的两点,为的中点,以线段BA,BC为邻边作菱形ABCD,顶点恰好为该圆直径的三等分点,则该菱形的边长为( )A、或 B、或 C、或 D、或二、填空题
-
9. 如图,已知的两弦相交于E , 且点A为的中点,若 , 则的度数为 .
 10. 如图,某地新建一座石拱桥,桥拱是圆弧形,它的跨度AB为60m, 拱高CD为10m, 则桥拱所在圆的半径长为
10. 如图,某地新建一座石拱桥,桥拱是圆弧形,它的跨度AB为60m, 拱高CD为10m, 则桥拱所在圆的半径长为
 11. 如图,都是的半径,交于点D . 若 , 则的长为
11. 如图,都是的半径,交于点D . 若 , 则的长为 12. 如图,已知圆O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP的长为.
12. 如图,已知圆O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP的长为.
三、解答题
-
13. 石拱桥是我国古代人民勤劳和智慧的结晶(如图①),赵州桥是我国古代石拱桥的代表,图②是根据该石拱桥画出的几何图形,桥的主桥拱是圆弧形,表示为 , 桥的跨度(弧所对的弦长) , 设所在圆的圆心为O , , 为半径,半径 , 垂足为D.拱高(弧的中点到弦的距离) .
 (1)、直接写出与的数量关系;(2)、求这座石拱桥主桥拱的半径.14. HUAWEIMate60Pro于8月29日上市,该系列完成了核心技术领域从0到1的跃迁,让无数国人为之自豪并被赞誉为“争气机”.手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量.圆弧对应的弦AB长80mm,弓形高CD长14mm求半径OA的长.
(1)、直接写出与的数量关系;(2)、求这座石拱桥主桥拱的半径.14. HUAWEIMate60Pro于8月29日上市,该系列完成了核心技术领域从0到1的跃迁,让无数国人为之自豪并被赞誉为“争气机”.手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量.圆弧对应的弦AB长80mm,弓形高CD长14mm求半径OA的长.
四、综合题

