【培优版】浙教版数学九上3.2 图形的旋转 同步练习
试卷更新日期:2024-09-10 类型:同步测试
一、选择题
-
1. 如图,将绕点顺时针旋转得到 , 并使点的对应点点落在直线上,连接 , 若 , 则的长为( )
 A、 B、15 C、 D、172. 如图,中, , 将绕点顺时针旋转得到 , 使点的对应点恰好落在边上,、交于点 . 若 , 则的度数是( )(用含的代数式表示)
A、 B、15 C、 D、172. 如图,中, , 将绕点顺时针旋转得到 , 使点的对应点恰好落在边上,、交于点 . 若 , 则的度数是( )(用含的代数式表示) A、 B、 C、 D、3. 如图,在中, , 点P是边上任意一点,将绕点C逆时针旋转得到 , 点P的对应点为点Q,连接 , 若 , 则的度数是( )
A、 B、 C、 D、3. 如图,在中, , 点P是边上任意一点,将绕点C逆时针旋转得到 , 点P的对应点为点Q,连接 , 若 , 则的度数是( ) A、 B、 C、 D、4. 如图,正方形的边长为4, , 将绕点按顺时针方向旋转得到 . 若 , 则的长为( )
A、 B、 C、 D、4. 如图,正方形的边长为4, , 将绕点按顺时针方向旋转得到 . 若 , 则的长为( )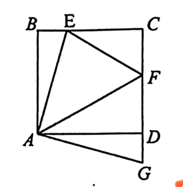 A、3 B、 C、 D、45. 如图,将含有角的直角三角板放置在平面直角坐标系中,在x轴上,若 , 将三角板绕原点O顺时针旋转 , 则点A的对应点的坐标为( )
A、3 B、 C、 D、45. 如图,将含有角的直角三角板放置在平面直角坐标系中,在x轴上,若 , 将三角板绕原点O顺时针旋转 , 则点A的对应点的坐标为( )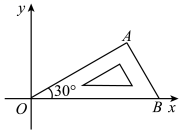 A、 B、 C、 D、6. 如图,正方形的顶点、在上,顶点、在内,将正方形绕点顺时针旋转 , 使点落在上.若正方形的边长和的半径相等,则旋转角度等于( )
A、 B、 C、 D、6. 如图,正方形的顶点、在上,顶点、在内,将正方形绕点顺时针旋转 , 使点落在上.若正方形的边长和的半径相等,则旋转角度等于( ) A、 B、 C、 D、7. 如图,平行四边形ABCD中,AB=16,AD=12,∠A=60°,E是边AD上一点,且AE=8,F是边AB上的一个动点,将线段EF绕点E逆时针旋转60°,得到EG , 连接BG、CG , 则BG+CG的最小值是( )
A、 B、 C、 D、7. 如图,平行四边形ABCD中,AB=16,AD=12,∠A=60°,E是边AD上一点,且AE=8,F是边AB上的一个动点,将线段EF绕点E逆时针旋转60°,得到EG , 连接BG、CG , 则BG+CG的最小值是( ) A、4 B、4 C、4 D、48. 如图,∠MAN=60°,点B、C分别在AM、AN上,AB=AC , 点D在∠MAN内部、△ABC外部,连接BD、CD、AD . 下列结论:①DB+DC≥DA;②S△BDC≤BD•DC;③若DB=m , DC=n , 则S△ADB≤+mn . 其中错误的结论个数为( )个.
A、4 B、4 C、4 D、48. 如图,∠MAN=60°,点B、C分别在AM、AN上,AB=AC , 点D在∠MAN内部、△ABC外部,连接BD、CD、AD . 下列结论:①DB+DC≥DA;②S△BDC≤BD•DC;③若DB=m , DC=n , 则S△ADB≤+mn . 其中错误的结论个数为( )个. A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
9. 如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为 .
 10. 如图,的顶点在抛物线上,将绕点顺时针旋转 , 得到 , 边与该抛物线交于点 , 则点的坐标为 .
10. 如图,的顶点在抛物线上,将绕点顺时针旋转 , 得到 , 边与该抛物线交于点 , 则点的坐标为 .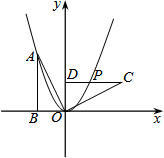 11. 如图,点A , C分别是y轴,x轴正半轴上的动点, , 将线段绕点A顺时针旋转60°得到线段 , 则的最小值是 .
11. 如图,点A , C分别是y轴,x轴正半轴上的动点, , 将线段绕点A顺时针旋转60°得到线段 , 则的最小值是 . 12. 如图,在Rt△ABC中,∠B=90°,AB=4,BC=6,点D在BC边上,将点A绕点D顺时针旋转90°得到点E,连接DE,CE.当△DCE是等腰三角形时,BD的长为 .
12. 如图,在Rt△ABC中,∠B=90°,AB=4,BC=6,点D在BC边上,将点A绕点D顺时针旋转90°得到点E,连接DE,CE.当△DCE是等腰三角形时,BD的长为 .
三、解答题
-
13. 已知线段和点 , 将线段绕点逆时针旋转 , 得到线段 , 将线段绕点顺时针旋转 , 得到线段 , 连接为的中点,连接 .
 (1)、如图1,点在线段上,依题意补全图1,直接写出的度数;(2)、如图2,点在线段的上方,写出一个的度数,使得成立,并证明.14. 如图,中, , 将绕点A逆时针旋转得到 , 与交于点D , 与交于点E , 与交于点F , 当B、D、F重合时停止旋转.
(1)、如图1,点在线段上,依题意补全图1,直接写出的度数;(2)、如图2,点在线段的上方,写出一个的度数,使得成立,并证明.14. 如图,中, , 将绕点A逆时针旋转得到 , 与交于点D , 与交于点E , 与交于点F , 当B、D、F重合时停止旋转. (1)、证明:在旋转过程中;(2)、如图1,当平分时,证明:;(3)、如图2,若 , , 在旋转过程中,当是等腰三角形时,求该等腰三角形底边的长度.
(1)、证明:在旋转过程中;(2)、如图1,当平分时,证明:;(3)、如图2,若 , , 在旋转过程中,当是等腰三角形时,求该等腰三角形底边的长度.四、实践探究题
-
15. 如图
图1
 图2
图2  图3
图3 (1)、【特例感知】如图 , 点是正方形对角线上一点,于点 , 于点.
(1)、【特例感知】如图 , 点是正方形对角线上一点,于点 , 于点.①求证:四边形是正方形;
②= ▲ ;
(2)、【规律探究】将正方形绕点旋转得到图 , 连接 , , .的比值是否会发生变化?说明理由;
(3)、【拓展应用】如图 , 在图的基础上,点 , , 分别是 , , 的中点;四边形是否是正方形?说明理由.16. 综合与探究. (1)、【问题情境】
(1)、【问题情境】数学活动课上,老师带领同学们一起探索旋转的奥秘.老师出示了一个问题:如图1所示,在中, , , 点是边上一点(),连接AD,将△ABD绕着点A按逆时针方向旋转,使AB与AC重合,得到△ACE.
连接 , 试判断的形状,并说明理由;
(2)、【深入探究】希望小组受此启发,如图2,在线段上取一点 , 连接 , 使得 , 连接 , 发现和有一定的关系,猜想两者的数量关系,并说明理由;
(3)、智慧小组在图2的基础上继续探究,发现 , , 三条线段之间也有一定的数量关系,请写出它们的数量关系,并说明理由.五、综合题
-
17. 综合与实践:如图(1),已知点E为正方形对角线上一动点(不与点C重合),连接 .
 (1)、实践与操作:在图中,画出以点B为旋转中心,将线段逆时针旋转的线段 , 并且连接 .(2)、观察与猜想:
(1)、实践与操作:在图中,画出以点B为旋转中心,将线段逆时针旋转的线段 , 并且连接 .(2)、观察与猜想:观察图(1),猜想并推理可以得到以下结论:
结论1,和之间的位置关系是;
结论2,和之间的数量关系是 .
(3)、探究与发现:①如图(2),若点E在延长线上时,(2)中的两个结论是否仍然成立,说明理由.
②如图(2),若 , , 请直接写出的长.
18. 如图①所示,将一个边长为2的正方形和一个长为2、宽为1的长方形拼在一起,构成一个大的长方形 . 现将小长方形绕点C顺时针旋转至长方形 , 旋转角为 .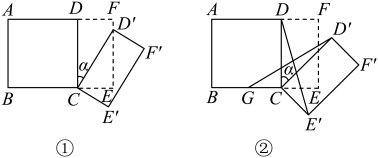 (1)、当点恰好落在边上时,求旋转角的值;(2)、如图②,G为中点,且 , 求证:;(3)、小长方形绕点C顺时针旋转一周的过程中,与能否全等?若能,直接写出旋转角的值;若不能,说明理由.
(1)、当点恰好落在边上时,求旋转角的值;(2)、如图②,G为中点,且 , 求证:;(3)、小长方形绕点C顺时针旋转一周的过程中,与能否全等?若能,直接写出旋转角的值;若不能,说明理由.