人教版九年级上学期数学第二十四章质量检测（初阶）
试卷更新日期：2024-09-09 类型：单元试卷
一、选择题
-
1. 如图，P为⊙O外一点，PA、PB分别切⊙O于点A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA＝6，则△PCD的周长为（ ）
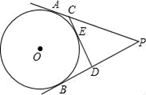A、8 B、6 C、12 D、102. 如图，四边形内接于 ， 若 ， 则的度数为（ ）
A、 B、 C、 D、3. 如图，已知是半的直径，是弦，切于点 ， 交的延长线于点 ， ， 则（ ）
A、 B、 C、 D、4. 如图，△ABC内接于⊙O，DE，FG是⊙O的弦，AB＝DE，FG＝AC．下列结论：①DE+FG＝BC；②+＝；③∠DOE+∠FOG＝∠BOC；④∠DEO+∠FGO＝∠BAC．其中所有正确结论的序号是（ ）
A、①②③④ B、②③ C、②④ D、②③④二、填空题
-
5. 一座拱桥的轮廓是一段半径为的圆弧（如图所示），桥拱和路面之间用数根钢索垂直相连，其正下方的路面长度为 ， 那么这些钢索中最长的一根为 ．
6. 若⊙O的半径为3，点P为平面内一点，OP＝2，那么点P在⊙O（填“上”、“内部”或“外部”）7. 如图，在正中，Q是边中点，P是边上任意一点，连接 ， 并使的延长线交的外角平分线于点G， ， 的外心在该三角形的内部，则的取值范围是 ．
三、解答题
-
8. 如图，为的直径，弦与交于点E， ， ．
(1)、求的度数；(2)、若 ， 求的长．9. 如图是一根圆形下水管道的横截面，管内有少量的污水，此时的水面宽为米，污水的最大深度为米．
(1)、求此下水管横截面的半径：(2)、随着污水量的增加，水位又被抬升米，求此时水面的宽度增加了多少？10. 如图，A是⊙O上一点，BC是直径，点D在⊙O上且平分 ．
(1)、连接AD ， 求∠BAD的度数；(2)、若 ， AB＝8，求AC的长．11. 已知是的直径，点D是延长线上一点， ， 是的弦， ．
(1)、求证：直线是的切线；(2)、若 ， 垂足为M ， 的半径为10，求的长．12. 如图 ， 小吴同学在陶艺课中为八角花盆制作“圆形托盘”，已知八角花盆底部截面是一个正八边形（如图），请根据下列信息解决问题．
(1)、求八角花盆底部截面正八边形一个内角的度数；(2)、若八角花盆底部截面正八边形的边长是 ， 小吴同学制作的圆形托盘半径是 ， 问：这个托盘是否适用于此八角花盆？（图中边长的数据为近似值，供选用）13. 如图1，圆形拱门屏风是家庭中常见的装饰隔断，既美观又实用，彰显出中国元素的韵味．如图2是一款拱门的示意图，其中C为的中点，D为拱门最高点，线段经过圆心O ， 已知拱门的半径为 ， 拱门最下端 ．
(1)、求拱门最高点D到地面的距离；(2)、现需要给房间内搬进一张长和宽均为、高为的桌子，已知搬桌子的两名工人在搬运时所抬高度相同，且高度为 ， 判断搬运该桌子时是否能够通过拱门．（参考数据：）