【培优版】北师大版数学八年级上册 4.1 函数 同步练习
试卷更新日期:2024-09-09 类型:同步测试
一、选择题
-
1. 下列曲线中不能表示y是x的函数的是( )A、
 B、
B、 C、
C、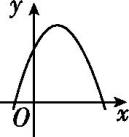 D、
D、 2. 函数自变量的取值范围是( )A、 B、 C、且 D、且3. 根据图中的程序,当输入x =3时,输出的结果y =( )
2. 函数自变量的取值范围是( )A、 B、 C、且 D、且3. 根据图中的程序,当输入x =3时,输出的结果y =( )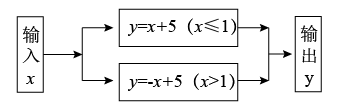 A、2 B、8 C、8或2 D、164. 杆秤是我国传统的计重工具.数学兴趣小组利用杠杆原理自制了一个如图1所示的无刻度简易杆秤.在量程范围内,之间的距离l与重物质量m的关系如图2所示,下列说法不正确的是( )
A、2 B、8 C、8或2 D、164. 杆秤是我国传统的计重工具.数学兴趣小组利用杠杆原理自制了一个如图1所示的无刻度简易杆秤.在量程范围内,之间的距离l与重物质量m的关系如图2所示,下列说法不正确的是( )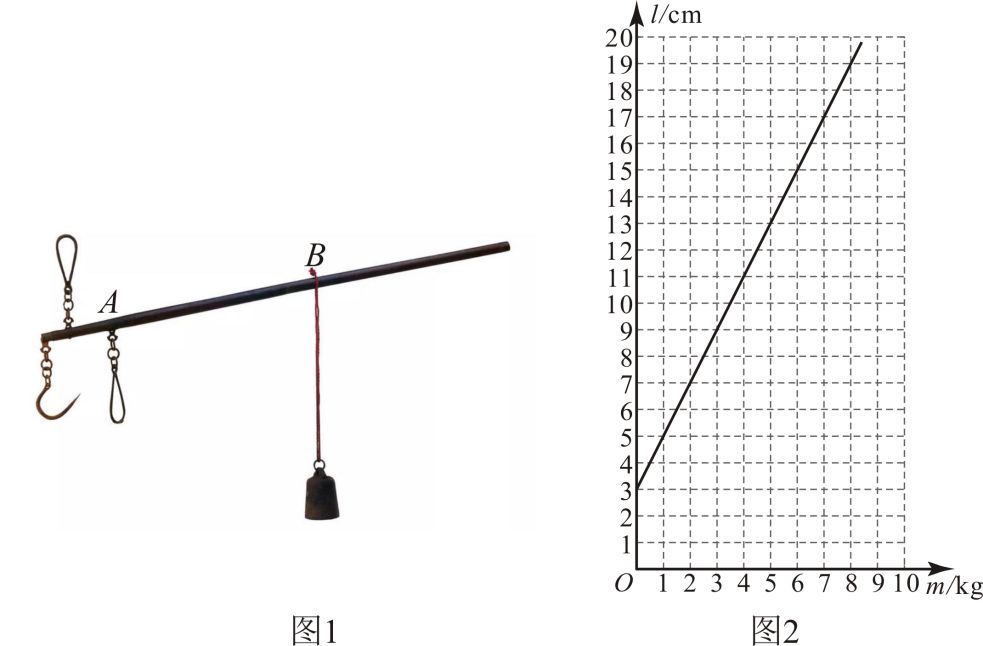 A、在量程范围内,质量m越大,之间的距离l越大; B、未挂重物时,之间的距离l为; C、当之间的距离l为时,重物质量m为; D、在量程范围内,重物质量m每增加 , 之间的距离l增加 .5. 如图(1),四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图(2)所示,当P运动到BC中点时,△APD的面积为( )
A、在量程范围内,质量m越大,之间的距离l越大; B、未挂重物时,之间的距离l为; C、当之间的距离l为时,重物质量m为; D、在量程范围内,重物质量m每增加 , 之间的距离l增加 .5. 如图(1),四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图(2)所示,当P运动到BC中点时,△APD的面积为( )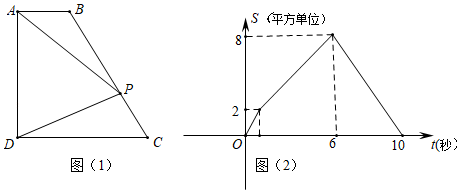 A、4 B、5 C、6 D、76. 如图①,在矩形中,动点从出发,以恒定的速度,沿方向运动到点处停止.设点运动的路程为 . 面积为 , 若与的函数图象如图②所示,则矩形的面积为( )
A、4 B、5 C、6 D、76. 如图①,在矩形中,动点从出发,以恒定的速度,沿方向运动到点处停止.设点运动的路程为 . 面积为 , 若与的函数图象如图②所示,则矩形的面积为( ) A、36 B、54 C、72 D、817. 高空抛物极其危险,是我们必须杜绝的行为.忽略空气阻力的影响,高空抛物的物体所在高度(单位:m)和下落的时间(单位:s)近似满足自由落体公式 , 其中 , 那么从高空抛物到落地的时间与从高空抛物到落地的时间之比的值为( )A、 B、 C、 D、8. 某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
A、36 B、54 C、72 D、817. 高空抛物极其危险,是我们必须杜绝的行为.忽略空气阻力的影响,高空抛物的物体所在高度(单位:m)和下落的时间(单位:s)近似满足自由落体公式 , 其中 , 那么从高空抛物到落地的时间与从高空抛物到落地的时间之比的值为( )A、 B、 C、 D、8. 某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):温度/℃
﹣20
﹣10
0
10
20
30
声速/m/s
318
324
330
336
342
348
下列说法错误的是( )
A、在这个变化中,自变量是温度,因变量是声速 B、温度越高,声速越快 C、当空气温度为20℃时,声音5s可以传播1740m D、当温度每升高10℃,声速增加6m/s二、填空题
-
9. 函数的自变量x的取值范围是 .10. 某图书出租店图书的租金y(元)与出租的天数x(天)之间的函数图象如图所示,结合图象计算可知:两天后每过一天租金增加元.
 11. 已知函数y= , 当x=时,y= .12. 两地相距的路程为240千米,甲、乙两车沿同一线路从 地出发到 地,分别以一定的速度匀速行驶,甲车先出发40分钟后,乙车才出发.途中乙车发生故障,修车耗时20分钟,随后,乙车车速比发生故障前减少了10千米/小时(仍保持匀速前行),甲、乙两车同时到达 地.甲、乙两车相距的路程 (千米)与甲车行驶时间 (小时)之间的关系如图所示,求乙车修好时,甲车距 地还有千米.
11. 已知函数y= , 当x=时,y= .12. 两地相距的路程为240千米,甲、乙两车沿同一线路从 地出发到 地,分别以一定的速度匀速行驶,甲车先出发40分钟后,乙车才出发.途中乙车发生故障,修车耗时20分钟,随后,乙车车速比发生故障前减少了10千米/小时(仍保持匀速前行),甲、乙两车同时到达 地.甲、乙两车相距的路程 (千米)与甲车行驶时间 (小时)之间的关系如图所示,求乙车修好时,甲车距 地还有千米. 13. 如图1,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水, 时注满水槽,水槽内水面的高度 与注水时间 之间的函数图象如图2所示.如果将正方体铁块取出,又经过秒恰好将水槽注满.
13. 如图1,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水, 时注满水槽,水槽内水面的高度 与注水时间 之间的函数图象如图2所示.如果将正方体铁块取出,又经过秒恰好将水槽注满.
三、解答题
-
14. 在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.
所挂物体
质量x/kg
0
1
2
3
4
5
弹簧长度
y/cm
18
20
22
24
26
28
①上述反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?②当所挂重物为3kg时,弹簧有多长?不挂重物呢?③若所挂重物为6kg时(在弹簧的允许范围内),你能说出此时弹簧的长度吗?
15. 汽车以70km/h的速度由A地驶往相距360km的B地,设汽车行驶的时间为t(h),离B地的距离为s(km).(1)、写出s关于t的函数表达式.(2)、写出自变量t的取值范围.(3)、求当t=2h时的函数值,并说明它的实际意义.16. 一水池的容积是 , 现蓄水 , 用水管以的速度向水池注水,直到注满为止.(1)、蓄水量与注水时间之间的关系式为.(2)、当时,.(3)、要注满水池容积的水,需要多少小时?17. 在一次实验中,小明把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.所挂物体质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
18
20
22
24
26
28
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当所挂物体重量为3千克时,弹簧多长?不挂重物时呢?
(3)若所挂重物为7千克时(在允许范围内),你能说出此时的弹簧长度吗?
18. 甲、乙两人从学校出发,沿相同的线路跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向体育馆,如图是甲、乙两人在跑步的全过程中经过的路程(米)与甲出发的时间(秒)的函数图象,请根据题意解答下列问题: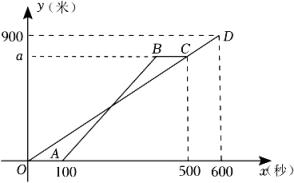 (1)、在跑步的全过程中,甲共跑了 米,甲的速度为 米/秒;(2)、乙最早出发时跑步的速度为 米/秒,乙在途中等候甲的时间为 秒;(3)、乙出发 秒后与甲第一次相遇;(4)、x=秒时,甲乙两人相距50米.
(1)、在跑步的全过程中,甲共跑了 米,甲的速度为 米/秒;(2)、乙最早出发时跑步的速度为 米/秒,乙在途中等候甲的时间为 秒;(3)、乙出发 秒后与甲第一次相遇;(4)、x=秒时,甲乙两人相距50米.