【培优卷】湘教版（2024）七年级上册4.1立体图形与平面图形 同步练习

试卷更新日期：2024-09-08 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 下列几何体的表面中，不含有曲面的是（　　）
    A、圆柱 B、四棱柱 C、圆锥 D、球体

    查看试题解析

  • 2. 下列几何体的展开图中，能围成四棱锥的是（    ）
    A、 B、 C、 D、

    查看试题解析

  • 3.  某几何体的表面展开图如图所示，这个几何体是（    ）

    A、圆柱 B、长方体 C、四棱锥 D、五棱锥

    查看试题解析

  • 4. 如图，下列四个图形是由①圆柱，②正方体，③三棱柱，④四棱锥的四个已知的立体图形展开得到的，则对应的标号依次是（ ）

    A、①②③④ B、②①③④ C、③②①④ D、④②①③

    查看试题解析

  • 5. 如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“我”字一面的相对面上的字是（   ）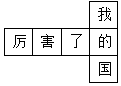

    A、厉 B、害 C、了 D、国

    查看试题解析

  • 6. 小欣同学用纸（如图）折成了个正方体的盒子，里面放了一瓶墨水，混放在下面的盒子里，只凭观察，选出墨水在哪个盒子中（    ）

    A、 B、 C、 D、

    查看试题解析

  • 7. 如图，是一个正方体的展开图，若相对面上的两个数互为相反数，则代数式2(a−b2)−3(b2+c)的值是（ ）

    A、6 B、−6 C、18 D、−18

    查看试题解析

  • 8. 如图是一个粉笔盒的表面展开图，若字母A表示粉笔盒的上盖，B表示侧面，则底面在表面展开图中的位置是（   ）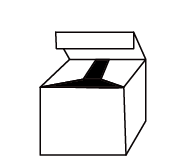

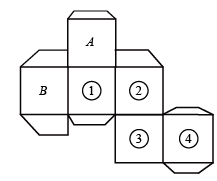    A、① B、② C、③ D、④

    查看试题解析

二、填空题

  • 9. 一个长方体，表面全部涂上红色后，被分割成若干个体积都等于 1 立方厘米的小正方体。如果在这些小正方体中， 不带红色的小正方体的个数等于 7 ， 那么两面带红色的小正方体的个数等于。

    查看试题解析

  • 10. 如图，四边形ABCD去掉∠C后，剩下的新图形是边形．

    查看试题解析

  • 11. 有一个正方体，六个面上分别写有数字1，2，3，4，5，6，如图是我们能看到的三种情况，如果记6的对面数字为a，2的对面数字为b，那么a+b的值为.

    查看试题解析

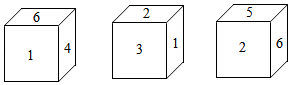  • 12. 某个长方体的展开图如图所示，各个面．上分别标有1~6的不同数字，若将其围成长方体，则这个长方体有公共顶点的三个面上的数字之和最大是 ．

    查看试题解析

  • 13. 如图，小强用5个大小一样的正方形制成如图所示的拼接图形（阴影部分），若在图中只添加一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子，这样的拼接方式有种．

    查看试题解析

三、解答题

  • 14.

    观察下图，思考问题：

    (1)、你认识上面的图片中的哪些物体？

    (2)、这些物体的表面形状类似与哪些几何体？说说你的理由。

    (3)、你能再举出一些常见的图形吗？​

    查看试题解析

  • 15. 李明同学设计了某个产品的正方体包装盒如图所示，由于粗心少设计了其中一个顶盖，请你把它补上，使其成为一个两面均有盖的正方体盒子．

    (1)、共有______种弥补方法；
    (2)、任意画出一种成功的设计图（在图中补充）；
    (3)、在你帮忙设计成功的图中，请把－6，8，10，－10，－8，6这些数字分别填入六个小正方形中，使得折成的正方体相对面上的两个数互为相反数．（直接在图中填上）

    查看试题解析

  • 16. 图①，图②，图③均为5×5的正方形网格，分别在3个网格中选择2个空白的正方形涂上阴影，使它们与图中四个有阴影的正方形共同构成一个正方体的表面展开图，并且3种方法得到的展开图不相同.

    查看试题解析

  • 17. 如图1，该三棱柱的高为9cm ， 底面是一个每条边长都为5cm的三角形．

      

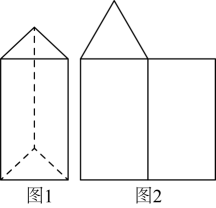    (1)、这个三棱柱有个面，有条棱．
    (2)、如图2，这是该三棱柱的表面展开图的一部分，请将它补充完整．
    (3)、这个三棱柱的侧面积是cm2 ， 要将该三棱柱的表面沿某些棱剪开，展开成一个平面图形，需剪开棱的棱长的和的最大值为cm ．

    查看试题解析

  • 18. 我校七年级（3）班数学活动小组的同学用纸板制作长方体包装盒，其平面展开图和相关尺寸如下，其中阴影部分为内部粘贴角料（单位：毫米）．

      

    (1)、此长方体包装盒的体积为立方毫米（用含x ， y的式子表示）．
    (2)、若内部粘贴角料的面积占长方体表面纸板面积的110 ， 则当x=5 ， y=15时，制作这样一个长方体共需要纸板多少平方毫米？

    查看试题解析

  • 19. 如图所示，若将类似于a、b、c、d四个图的图形称做平面图，则其顶点数、边数与区域数之间存在某种关系．观察图b和表中对应的数值，探究计数的方法并作答．

    (1)、数一数每个图中各有多少个顶点、多少条边，这些边围出多少个区域并填表：

    图

     a

    b

     c

     d

     顶点数（S）

     7

     边数（M）

     9

     区域数（N）

     3

    (2)、根据表中数值，写出平面图的顶点数、边数、区域数之间的一种关系；
    (3)、如果一个平面图有20个顶点和11个区域，那么利用（2）中得出的关系可知这个平面图有条边．

    查看试题解析

  • 20. 某“综合实践”小组开展了“长方体纸盒的制作”实践活动，他们利用边长为a（cm）的正方形纸板制作出两种不同方案的长方体盒子（图1为无盖的长方体纸盒，图2为有盖的长方体纸盒）．

    【操作一】根据图1方式制作一个无盖的长方体盒子．方法：先在纸板四角剪去四个同样大小边长为b（cm）的小正方形，再沿虚线折合起来．

    (1)、【问题解决】若a＝12cm，b＝3cm，则长方体纸盒的底面积为 ；
    (2)、【操作二】根据图2方式制作一个有盖的长方体纸盒．方法：先在纸板四角剪去两个同样大小边长为b（cm）的小正方形和两个同样大小的小长方形，再沿虚线折合起来．
    【拓展延伸】若a＝12cm，b＝2cm，该长方体纸盒的体积为 ；
    (3)、现有两张边长a均为30cm的正方形纸板，分别按图1、图2的要求制作无盖和有盖的两个长方体盒子，若b＝5cm，求无盖盒子的体积是有盖盒子体积的多少倍？

    查看试题解析