【培优卷】湘教版（2024）七年级上册第二章代数式单元测试

试卷更新日期：2024-09-08 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列用数学式子表示数量关系不正确的是（）

A、a与b的差的2倍，表示为 $a - b \times 2$ B、x的2倍与y的 $\frac{1}{3}$ 的和，表示为 $2 x + \frac{1}{3} y$ C、比x的 $\frac{3}{2}$ 倍大5的数，表示为 $\frac{3}{2} x + 5$ D、比x的3倍小6的数，表示为3x－6

查看试题解析
2. 下列说法正确的是（）

A、﹣πab的次数为3 B、2a+ab﹣12是二次三项式 C、 $\frac{a b}{5}$ 的系数为5 D、﹣a³b和ab³同类项

查看试题解析
3. 已知式子 $y^{2} - 2 y + 6$ 的值为 $8$ ，那么式子 $- 2 y^{2} + 4 y + 5$ 的值为（）

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
4. 多项式x⁵y²+2x⁴y³﹣3x²y²﹣4xy是（　　）

A、按x的升幂排列 B、按x的降幂排列 C、按y的升幂排列 D、按y的降幂排列

查看试题解析
5. 如图，是一个数据运算程序，如果开始输入的x的值为10，那么第1次输出的结果是5，返回进行第二次运算，则第2次输出的结果是16，……以此类推，第2023次输出的结果是（　　）

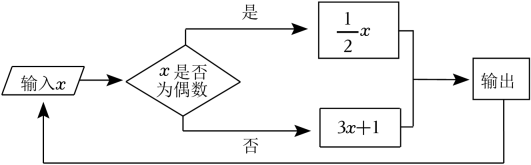A、16 B、8 C、4 D、2

查看试题解析
6. 已知 $a_{1} = 3 ， a_{2} = \frac{1}{1 - a_{1}} ， a_{3} = \frac{1}{1 - a_{2}} ， a_{4} = \frac{1}{1 - a_{3}} ， \cdot \cdot \cdot$ ，依此类推，则 $a_{2024}$ 等于（）．

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、3

查看试题解析
7. 已知一个多项式与 $(2 x^{2} + 3 x - 4)$ 的和为 $(2 x^{2} + x - 2)$ ，则此多项式是（）

A、 $2 x + 2$ B、 $- 2 x + 2$ C、 $- 2 x - 2$ D、 $2 x - 2$

查看试题解析
8. 如图，一个大正方形的四个角落分别放置了四张大小不同的正方形纸片，其中1号，2号两张正方形纸片既不重叠也无空隙．已知1号正方形边长为a ， 2号正方形边长为b ，则阴影部分的周长是（）

A、2a+2b B、4a+2b C、2a+4b D、3a+3b

查看试题解析
9. 将四张边长各不相同的正方形纸片按如图方式放入长方形 $A B C D$ 内（相邻纸片之间互不重叠也无缝隙），未被四张正方形纸片覆盖的部分用阴影表示．若要知道右上角与左下角阴影部分的周长的差，则只需测量编号为____的一个正方形的边长．（填编号）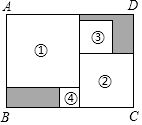

A、① B、② C、③ D、④

查看试题解析
10. 对任意代数式，每个字母及其左边的符号（不包括括号外的符号）称为一个数，如： $a - (b + c) - (- d - e)$ ，其中称 $a$ 为“数1”， $b$ 为“数2”， $+ c$ 为“数3”， $- d$ 为“数4”， $- e$ 为“数5”，若将任意两个数交换位置，则称这个过程为“换位思考”，例如：对上述代数式的“数1”和“数5”进行“换位思考”，得到： $- e - (b + c) - (- d + a)$ ，则下列说法中正确的个数是（）
①代数式 $(a - b) + (c - d) - e$ 进行一次“换位思考”，化简后只能得到1种结果②代数式 $a - (b + c - d - e)$ 进行一次“换位思考”，化简后可能得到5种结果③代数式 $a + [b - (c - d - e)]$ 进行一次“换位思考”，化简后可能得到7种结果④代数式 $a - [b + c - (d - e)]$ 进行一次“换位思考”，化简后可能得到8种结果

A、0 B、2 C、3 D、4

查看试题解析

二、填空题（每题3分，共18分）

11. 请你写出一个只含有字母 $a$ ， $b$ ，且它的系数为 $- 3$ 、次数为 $3$ 的单项式．

查看试题解析
12. 若 $2 a^{m + 1} b^{2}$ 与 $- 3 a^{3} b^{n}$ 是同类项，则 $m + n$ 的值为．

查看试题解析
13. 已知关于x，y的代数式ax²+2x+x²﹣3y²﹣bx+4y﹣5的值与x的取值无关，则a﹣b= ．

查看试题解析
14. 小程做一道题“已知两个多项式 $A$ ， $B$ ，计算 $A - B$ ”，小程误将 $A - B$ 看成了 $A + B$ ，求得的结果是 $9 x^{2} - 2 x + 7$ ．若 $B = x^{2} + 3 x - 2$ ，则 $A - B =$ ．

查看试题解析
15. 如图所示，在长方形 $A B C D$ 中， $A D = 3 A B$ ，在它内部有三个小正方形，正方形 $A E F G$ 的边长为m，正方形 $G B I H$ 的边长为n，则阴影部分的周长为（用含m，n的代数式表示）．

查看试题解析
16. 已知有理数a，b，c在数轴上对应点分别为A，B，C，点A，B在数轴上的位置如图所示．若 $|b| = 5, A C = 2$ ，则 $a + b - c$ 的值为．

查看试题解析

三、解答题（共9题，共72分）

17. 化简：

(1)、 $2 x^{2} - 2 x + 4 x^{2} - x$

(2)、 $3 a^{2} - [2 a - (\frac{1}{2} a - 3) + 2 a^{2}]$

查看试题解析
18. 先化简，再求值： $\frac{1}{2} x - 2 (x - \frac{1}{3} y^{2}) + (- \frac{3}{2} x + \frac{1}{3} y^{2}) ，$ 其中 $x = \frac{2}{3} ， y = - 2.$

查看试题解析
19.

(1)、已知 $A = 3 x - 4 x y + 2 y$ ，小明在计算 $2 A - B$ 时，误将其按 $2 A + B$ 计算，结果得到 $7 x + 4 x y - y$ ．求多项式 $B$ ，并计算出 $2 A - B$ 的正确结果．

(2)、已知 $A = b y^{2} - a y - 1$ ， $B = 2 y^{2} + 3 a y - 10 y + 3$ ．若多项式 $2 A - B$ 的值与字母 $y$ 的取值无关，求 $a$ 、 $b$ 的值．

查看试题解析
20. 阅读计算 $(- 3 x^{3} + 5 x^{2} - 7) + (2 x - 3 + 3 x^{2})$ 时，可列竖式（如图）

小明认为，整式的加减实际上就是合并同类项，而合并同类项的关键是合并各同类项的系数，因此，可以把上题的竖式简化为右上图形式，所以，原式 $= - 3 x^{3} + 8 x^{2} + 2 x - 10$ ．
根据阅读材料解答下列问题：已知： $A = 2 x^{4} - 3 - x - 3 x^{3}$ ， $B = x^{3} - x^{2} + 2 x$ ．

(1)、将A按x的降幂排列：；

(2)、请仿照小明的方法计算： $A - B$ ；

(3)、请写出一个多项式C：，使其与B的和是四次三项式．

查看试题解析
21. 阅读材料：“如果代数式 $5 a + 3 b$ 的值为 $- 4$ ，那么代数式 $2 (a + b) + 4 (2 a + b)$ 的值是多少？”
我们可以这样来解：原式 $= 2 a + 2 b + 8 a + 4 b = 10 a + 6 b$ ．把式子 $5 a + 3 b = - 4$ 两边同乘以2，得 $10 a + 6 b = - 8$ ．
仿照上面的解题方法，完成下面的问题：

(1)、已知 $a^{2} + a = 2$ ，求 $a^{2} + a + 2024$ 的值；

(2)、已知 $a - b = - 4$ ，求 $3 (a - b) - a + b + 9$ 的值；

(3)、已知 $a^{2} + 2 a b = - 2$ ， $a b - b^{2} = - 4$ ，求 $2 a^{2} + 5 a b - b^{2}$ 的值．

查看试题解析
22. 探索代数式a²-2ab+b²与代数式（a-b）²的关系．

(1)、当a＝2，b＝1时分别计算两个代数式的值．

(2)、当a＝3，b＝-2时分别计算两个代数式的值．

(3)、你发现了什么规律？

(4)、利用你发现的规律计算：2023²-2×2023×2022+2022² ．

查看试题解析
23. 阅读理解：若在一个两位正整数N的个位数字与十位数字之间添上数字6，组成一个新的三位数，我们称这个三位数为N的“至善数”，如34的“至善数为364”；若将一个两位正整数M加6后得到一个新数，我们称这个新数为M的“明德数”，如34的“明德数为40”.

(1)、30的“至善数”是， “明德数”是.

(2)、求证：对任意一个两位正整数A，其“至善数”与“明德数”之差能被9整除；

(3)、若一个两位正整数B的明德数的各位数字之和是B的至善数各位数字之和的一半，求B的最大值.

查看试题解析

24. 滴滴快车是一种便捷的出行工具，计价规则如下表：

计费项目	里程费	时长费	远途费
单价	$1.8$ 元/公里	$0.45$ 元/分钟	$0.4$ 元/公里
注：车费由里程费、时长费、远途费三部分构成，其中里程费按行车的实际里程计算：时长费按行车的实际时间计算；远途费的收取方式为：行车里程10公里以内（含10公里）不收远途费，超过10公里的，超出部分每公里收 $0.4$ 元．

(1)、若小东乘坐滴滴快车，行车里程为15公里，行车时间为20分钟，则需付车费多少元?

(2)、若小明乘坐滴滴快车，行车里程为

a

公里，行车时间为

b

分钟，则小明应付车费多少元（用含

a

、

b

的代数式表示，并化简）?

(3)、小王与小张各自乘坐滴滴快车，行车里程分别为

9.5

公里与

14.5

公里，但下车时两人所付车费相同，那么这两辆滴滴快车的行车时间相差多少分钟?

查看试题解析

25. 我市某小区居民使用自来水2023年标准缴费如下（水费按月缴纳）：
用户月用水量
单价
不超过 $12 m^{3}$ 的部分
$a$ 元 $/ m^{3}$
超过 $12 m^{3}$ 但不超过 $20 m^{3}$ 的部分
$1.5 a$ 元 $/ m^{3}$
超过 $20 m^{3}$ 的部分
$2 a$ 元 $/ m^{3}$

(1)、当 $a = 2$ 时，
①某户1月份用了 $3 m^{3}$ 的水，求该户1月份应缴纳的水费__________元．
②某户4月份用了 $13 m^{3}$ 的水，求该户4月份应缴纳的水费__________元．
③某户8月份用了 $23 m^{3}$ 的水，求该户8月份应缴纳的水费__________元．

(2)、设某户月用水量为 $n m^{3}$ ，当 $n > 20$ 时，该户应缴纳的水费为__________元（用含 $a$ ， $n$ 的式子表示）．

(3)、当 $a = 2$ 时，甲、乙两户一个月共用水 $40 m^{3}$ ，已知甲户缴纳的水费超过了24元，设甲户这个月用水 $x m^{3}$ ，试求甲，乙两户一个月共缴纳的水费（用含 $x$ 的式子表示）

查看试题解析

用户月用水量	单价
不超过 $12 m^{3}$ 的部分	$a$ 元 $/ m^{3}$
超过 $12 m^{3}$ 但不超过 $20 m^{3}$ 的部分	$1.5 a$ 元 $/ m^{3}$
超过 $20 m^{3}$ 的部分	$2 a$ 元 $/ m^{3}$

【培优卷】湘教版（2024）七年级上册第二章 代数式 单元测试

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共9题，共72分）

【培优卷】湘教版（2024）七年级上册第二章代数式单元测试