【基础卷】湘教版（2024）七年级上册第二章代数式单元测试

试卷更新日期：2024-09-08 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列代数式书写规范的是（　　）

A、8x²y B、1 $\frac{2}{3}$ b C、ax3 D、2m÷n

查看试题解析
2. 某电子产品原价为m ， 9月迎来开学季，商家开展“教育优惠”活动，现售价为 $0.8 m - 100$ 则下列说法中，符合题意的是（）

A、原价减100元后再打8折 B、原价打8折后再减100元 C、原价打2折后再减100元 D、原价减100元后再打2折

查看试题解析
3. 随着服装市场竞争日益激烈，某品牌服装专卖店一款服装按原售价降价 $30 %$ ，现售价为 $a$ 元，则原售价为（）

A、 $(a - 30 %)$ 元 B、 $(a + 30 %)$ 元 C、 $\frac{10}{7} a$ 元 D、 $\frac{7}{10} a$ 元

查看试题解析
4. 已知 $x - 2 y = - 1$ ，则 $- 4 x + 8 y + 15$ 的值是（　　）

A、11 B、14 C、10 D、19

查看试题解析
5. 如图所示是一个计算机程序图，如果开始输入 $x = 0$ ，那么最后输出的结果为（　　）

A、 $- 2$ B、1 C、 $- 5$ D、 $- 1$

查看试题解析
6. 如果a与 $- 3$ 互为相反数，那么 $a + 4 =$ （）

A、 $- 7$ B、1 C、 $\frac{1}{2}$ D、7

查看试题解析
7. 下列代数式中，是次数为3的单项式的是（）

A、 $- m^{3} n$ B、3 C、 $4 t^{3} - 3$ D、 $\frac{x^{2} y}{2}$

查看试题解析
8. 下列计算正确的是（）

A、 $m^{2} n - 2 m n^{2} = - m n^{2}$ B、 $5 y^{2} - 2 y^{2} = 3$ C、 $7 a + a = 7 a^{2}$ D、 $3 a b + 2 a b = 5 a b$

查看试题解析
9. 与 $- 2 (a + b)$ 相等的是（）

A、 $- 2 a - b$ B、 $- 2 a + b$ C、 $- 2 a - 2 b$ D、 $- 2 a + 2 b$

查看试题解析
10. 某商店在甲批发市场以每包 $a$ 元的价格购进 $35$ 包茶叶，又在乙批发市场以每包 $b (a > b)$ 元的价格购进同样的茶叶 $25$ 包，如果以每包 $\frac{1}{3} (2 a + b)$ 元的价格全部卖出这种茶叶，那么这家商店在这次交易中（）

A、盈利了 B、亏损了 C、不盈不亏 D、不能确定

查看试题解析

二、填空题（每题3分，共18分）

11. 为了帮助地震灾区重建家园，某班全体师生积极捐款，捐款金额共3150元，其中5名教师人均捐款a元，则该班学生共捐款元（用含有a的代数式表示）．

查看试题解析
12. 若某三位数的个位数字为a，十位数字为b，百位数字为c，则这个三位数可表示为．

查看试题解析
13. 某品牌电脑原售价降低M元之后，又降价 $10 %$ ，现售价N元，则该电脑原售价为元

查看试题解析
14. 若 $a - 3 b = - 5$ ，则 $2 {(a - 3 b)}^{2} + 3 b - a - 15 =$ ．

查看试题解析
15. 多项式 $\frac{5 x^{2} - 2}{7}$ 的常数项是．

查看试题解析
16. 若关于 $x$ 的两个多项式 $x^{3} - 8 x^{2} + x + 2$ 与 $2 x^{3} + 2 m x - 3 x - 1$ 的和为三次三项式，则 $m$ 的值为．

查看试题解析

三、解答题（共9题，共72分）

17. 下列代数式中哪些是单项式？哪些是多项式？分别填入所属的圈中，指出其中各单项式的系数；多项式中哪个次数最高？次数是多少？
$- 15 a^{2} b$ ， $\frac{3 x^{2}}{π}$ ， $2 x - 3 y$ ， $4 a^{2} b^{2} - 4 a b + b^{2}$ ， $- a$ ， $x^{3} + 2 y - x$ .

查看试题解析
18. 多项式 $- 2 + x^{n - 1} y + x^{n - 1} - n x^{2} y^{n - 1}$ 是关于x、y的四次三项式.

(1)、求m和 $n$ 的值；

(2)、将这个多项式按字母 $x$ 的降排列，并直接写出它的常数项.

查看试题解析
19. 化简下列各式：

(1)、（2a﹣b）﹣（2b+3a）﹣2（a﹣2b）；

(2)、（4x²﹣3x+1）﹣2（x²+2x﹣1）．

查看试题解析
20. 某同学做一道数学题，已知两个多项式 $A 、 B$ ，其中 $B = 2 x^{2} y - 3 x y + 2 x + 5$ ，试求 $A + B$ ．这位同学把 $A + B$ 误看成 $A - B$ ，结果求出的答案为 $4 x^{2} y + x y - x - 4$ ．

(1)、请你替这位同学求出 $A + B$ 的正确答案；

(2)、若 $A - 3 B$ 的值与 $x$ 的取值无关，求 $y$ 的值．

查看试题解析
21. 如图，这是一套商品房的平面图 $($ 阴影部分 $) ($ 单位： $m)$ ．

(1)、求这套房子的总面积 $($ 用含 $x$ 、 $y$ 的式子表示 $)$ ；

(2)、若 $x = 5$ ， $y = 8$ ，且房价为每平方米 $3.2$ 万元，求购买这套房子共需要多少万元？

查看试题解析

22. 滴滴快车是一种便捷的出行工具，计价规则如表：

计费项目	里程费	时长费	远途费
单价	1.8元/公里	0.3元/分钟	0.8元/公里
注：车费由里程费、时长费、远途费三部分构成，其中里程费按行车的实际里程计算，时长费按行车的实际时间计算，远途费的收取方式为：行车里程7公里以内（含7公里）不收远途费，超过7公里的，超出部分每公里加收0.8元．

小明与小亮各自乘坐滴滴快车，到同一地点约见，已知到达约见地点时他们的实际行车里程分别为6公里与8.5公里．设小明乘车时间为x分钟，小亮乘车时间为y分钟．

(1)、则小明乘车费为元（用含x的代数式表示），小亮乘车费为元（用含y的代数式表示）；

(2)、若小明比小亮少支付3元钱，问小明与小亮的乘车时间哪个多？多几分钟？

查看试题解析

23. 如图所示，某数学活动小组编制了一道有理数混合运算题，即输入一个有理数，按照自左向右的顺序运算，可得计算结果，其中“”表示一个有理数.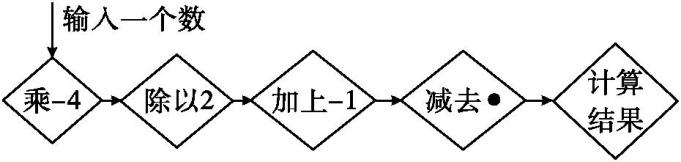

(1)、若表示2，输入的数为-3，求计算结果；

(2)、若计算结果为8，且输入的数是4，则表示的数是多少?

(3)、若输入的数为a，表示的数为b，当计算结果为0时，求出a与b之间的数量关系.

查看试题解析
24. 某校举行了“喜迎二十大”知识竞赛，并设立了一、二、三等奖，根据设奖情况买了50件奖品，其中二等奖奖品的件数比一等奖奖品件数的2倍少8件，各种奖品的单价如下表所示：

一等奖奖品
二等奖奖品
三等奖奖品
单价（单位：元）
15
12
8
数量（单位：件）
x
m
n

(1)、求表格中m ， n的值（用含x的式子表示）；

(2)、用含x的式子表示购买这50件奖品所需总费用（化成最简）；

(3)、若一等奖奖品购买了10件，求该校购买这50件奖品共花费多少元?

查看试题解析
25. 某大型商场销售一种茶具和茶碗，茶具每套定价300元，茶碗每只定价40元，“双十一”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案：
方案一：买一套茶具送2只茶碗；
方案二：茶具和茶碗都按定价的八五折付款．
现在某客户要到商场购买茶具20套，茶碗 $x (x > 40)$ 只．

(1)、分别用含有 $x$ 的代数式表示用两种方案购买所需的费用；

(2)、当 $x = 50$ 时，客户选用哪种方案比较实惠？请说明理由．

查看试题解析

	一等奖奖品	二等奖奖品	三等奖奖品
单价（单位：元）	15	12	8
数量（单位：件）	x	m	n

【基础卷】湘教版（2024）七年级上册第二章 代数式 单元测试

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共9题，共72分）

【基础卷】湘教版（2024）七年级上册第二章代数式单元测试