【培优卷】湘教版（2024）七年级上册2.2代数式的值同步练习

试卷更新日期：2024-09-08 类型：同步测试

进入出卷网下载

一、选择题

1. 若代数式 $x^{2} - 3 x$ 的值为 $- 2$ ，则 $2 x^{2} - 6 x - 8$ 的值为（）

A、12 B、4 C、 $- 4$ D、 $- 12$

查看试题解析
2. 当x＝2时，代数式x³+mx³+x-1的值为10，则x＝-2时，x³+mx³+x-1的值为（　　）

A、10 B、-10 C、-11 D、-12

查看试题解析
3. 已知|x|＝3，|y|＝5，且|x+y|＝x+y ，则x﹣y的值为（）

A、±2 B、±2或±8 C、﹣2或﹣8 D、﹣2或8

查看试题解析
4. 若 $| a | = 5$ ， $| b | = 3$ ，那么 $a \times b$ 的值有（）个

A、2 B、3 C、4 D、5

查看试题解析
5. 如图是一个运算程序，若第1次输入 $a$ 的值为16，则第2024次输出的结果是（）

A、1 B、2 C、4 D、8

查看试题解析
6. 已知代数式 $3 x^{2} - 3 x + 2$ 的值为 $7$ ，则代数式 $- x^{2} + x$ 的值为（）

A、 $- \frac{5}{3}$ B、 $\frac{5}{3}$ C、 $5$ D、 $- 5$

查看试题解析
7. 若 $x - 3 y = - 4$ ，则 $(x - 3 y)^{2} + 2 x - 6 y - 10$ 的值为（）

A、 $14$ B、 $2$ C、 $- 18$ D、 $- 2$

查看试题解析
8. 若2023×7=x，则下列代数式可以表示2023×5是（　　）

A、 $x + 4046$ B、 $x - 4046$ C、 $x - 2$ D、 $x + 2$

查看试题解析

二、填空题

9. 当 $x = 1$ 时， $k x + b$ 的值为6，则 $3 - k - b$ 的值是．

查看试题解析
10. 如果实际值为a ，测量值为b ，我们把 $| a - b |$ 称为绝对误差， $\frac{| a - b |}{a}$ 称为相对误差．若有种零件实际长度为 $10.0 c m$ ，测量得 $9.9 c m$ ，则测量所产生的相对误差是．

查看试题解析
11. 赋值法是给代数式中的某些字母赋予一定的特殊值，从而解决问题的一种方法，已知 ${(2 x - 3)}^{2} = a x^{2} + b x + c$ ．例如：给 $x$ 赋值使 $x = 0$ ﹐则可求得 $c = 9$ ；给 $x$ 赋值使 $x = 1$ ，则可求得 $a + b + c = 1$ ；给 $x$ 赋值使 $x = - 1$ ，则可以求得代数式 $a - b$ 的值为．

查看试题解析
12. 在如图程序中，“ ”处x前面的系数由于乱码无法显示．已知输入2023时，输出结果为5，则输入 $- 2023$ 时，输出结果为．

查看试题解析
13. 如图，将两张边长分别为5和4的正方形纸片分别按图①和图②两种方式放置在长方形内（图①和图②中两张正方形纸片均有部分重叠），未被这两张正方形纸片覆盖的部分用阴影表示．若长方形中边 $A B$ ， $A D$ 的长度分别为 $m ， n$ ．设图①中阴影部分面积为 $S_{1}$ ，图②中阴影部分面积为 $S_{2}$ ，当 $m - n = 4$ 时， $S_{1} - S_{2}$ 的值为．

查看试题解析

三、解答题

14. 已知 $|a| = 2$ ， $|b| = 5$ ．

(1)、若 $a < b$ ，求 $a^{2} + b$ 的值；

(2)、若 $|a - b| = a - b$ ，求 $a + b$ 的值．

查看试题解析
15. 九龙商场电器销售一种微波炉和电磁炉.微波炉每台定价700元，电磁炉每台定价200元.国庆节期间商场决定开展促销活动，活动期间向客户提供两种优惠方案.
方案一：参加“买1送1”活动，买一台微波炉送一台电磁炉；
方案二：参加“8折优惠”活动，微波炉和电磁炉都按定价的80%付款.
现某客户要到该卖场购买微波炉20台，电磁炉 $x$ 台（ $x > 20$ ）.

(1)、若该客户按方案一购买，需付款元.（用含 $x$ 的代数式表示），若该客户按方案二购买，需付款元.（用含 $x$ 的代数式表示）

(2)、若 $x = 50$ ，通过计算说明此时按哪种方案购买较为合算？

(3)、当 $x = 50$ 时，你能给出一种更为省钱的购买方案吗？试写出你的购买方案.

查看试题解析
16. 我们知道： $10 a + 2 a - a = (10 + 2 - 1) a = 11 a$ ，类似地，若我们把 $(x + y)$ 看成一个整体，则有 $10 (x + y) + 2 (x + y) - (x + y) = (10 + 2 - 1) (x + y) = 11 (x + y)$ ，这种解决问题的方法渗透了数学中的“整体思想”．“整体思想”是中学数学解题中的一种重要的思想方法，其应用极为广泛．请运用“整体思想”解答下面的问题：

(1)、把 ${(m - n)}^{2}$ 看成一个整体，合并 $3 {(m - n)}^{2} - \frac{1}{2} {(m - n)}^{2} + 2 {(m - n)}^{2}$ ；

(2)、已知： $x^{2} + 2 y = 3$ ，求代数式 $- 3 x^{2} - 6 y + 2$ 的值；

(3)、已知 $a - 2 b = 3$ ， $2 b - c = - 5$ ， $c - d = 9$ ，求 $(a - c) + (2 b - d) - (2 b - c)$ 的值．

查看试题解析
17. 综合与实践
问题情境：
在数学活动课上，老师让同学们制作了一些边长为 $20 c m$ 的正方形纸片，并要求各个小组利用这些纸片研究数学问题．
实践操作：

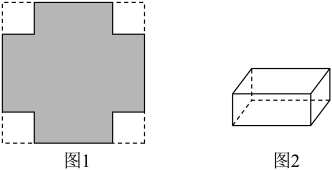(1)、勤勉小组提出：将如图1所示的纸片的四个角各剪去一个相同的正方形，得到图1中的阴影部分，若剪去的小正方形的边长为 $x c m$ ，请计算阴影部分的面积S（用含 $x$ 的式子表示），并求出当 $x = 3$ 时，阴影部分的面积；

(2)、创新小组将图1中的阴影部分折成一个无盖的长方体盒子，如图2，请求出折成的长方体盒子的容积V（用含 $x$ 的式子表示），并求出当 $x = 3$ 时，折成的长方体盒子的容积．

查看试题解析
18. 综合与实践
某兴趣小组利用长为a厘米，宽为b厘米的长方形纸板制作长方体纸盒，做了以下尝试：（纸板厚度及接缝处忽略不计）

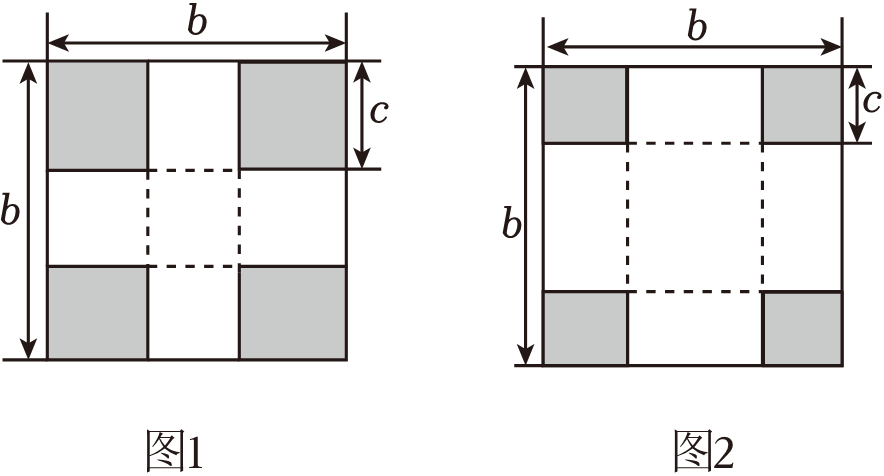(1)、如图1，若a=b，先在纸板四角剪去4个同样大小边长为c厘米的小正方形，再沿虚线折起来就可以做成一个无盖的正方体纸盒．此时，b与c的数量关系为．

(2)、如图2，若a=b，先在纸板四角剪去4个同样大小边长为c厘米的小正方形，再沿虚线折起来就可以做成一个无盖的长方体纸盒，为了使纸盒底面更加牢固且达到废物利用的目的，将剪下的四个小正方形平铺在盒子的底面，要求既不重叠又恰好铺满．此时，b与c的数量关系为．

(3)、若a=20，b=12，在纸板四角剪去4个同样大小边长为c厘米的小正方形，恰好可以制作成一个无盖的长方体纸盒．请你通过列表研究，c取何整数时，所得长方体的体积V最大？
c/cm

V/cm³

查看试题解析

c/cm
V/cm³

【培优卷】湘教版（2024）七年级上册2.2代数式的值 同步练习

一、选择题

二、填空题

三、解答题

【培优卷】湘教版（2024）七年级上册2.2代数式的值同步练习