【培优版】新北师大版（2024）数学七年级上册第四章 平面基本图形 章节测试卷
试卷更新日期：2024-09-07 类型：单元试卷
一、选择题(本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）
-
1. OB是∠AOC内部一条射线，OM是∠AOB平分线，ON是∠AOC平分线，OP是∠NOA平分线，OQ是∠MOA平分线，则∠POQ：∠BOC＝（ ）
A、1：2 B、1：3 C、2：5 D、1：42. 平面内的9条直线任两条都相交，交点数最多有m个，最少有n个，则m+n等于（ ）A、36 B、37 C、38 D、393. 已知A，B，C三点， ， ，则 （ ）A、8cm B、4cm C、8cm或4cm D、无法确定4. 如图所示，某工厂有三个住宅区，A，B，C各区分别住有职工30人，15人，10人，且这三点在一条大道上（A，B，C三点在同一直线上），已知AB＝300米，BC＝600米．为了方便职工上下班，该厂的接送车打算在此路段只设一个停靠点，为使所有的人步行到停靠点的路程之和最小，那么该停靠点的位置应设在（ ）
A、点A B、点B C、AB之间 D、BC之间5. 当式子|x+1|+|x﹣6|取得最小值时，x的取值范围为（ ）A、﹣1≤x＜6 B、﹣1≤x≤6 C、x=﹣1或x=6 D、﹣1＜x≤66. 一个多边形最少可分割成五个三角形，则它是（ ）边形A、8 B、7 C、6 D、57. 如图，一扇形纸扇完全打开后，外侧两竹条AB和AC的夹角为120°，AB长为25cm，贴纸部分的宽BD为15cm，若纸扇两面贴纸，则贴纸的面积为（ ）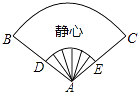
A、175πcm2 B、350πcm2 C、 πcm2 D、150πcm28. 如图，点 为线段 外一点，点 ， ， ， 为 上任意四点，连接 ， ， ， ，下列结论错误的是（ ）
A、以 为顶点的角共有15个 B、若 ， ，则 C、若 为 中点， 为 中点，则 D、若 平分 ， 平分 ， ，则二、填空题（每题3分，共15分）
-
9. 如图，在∠AOB的内部有3条射线OC，OD，OE．若∠AOC= 51°，∠BOE =∠BOC，∠BOD=∠AOB，则∠DOE=°
10. 5时15分＝时，4吨90千克＝吨．11. 一个六边形共有条对角线.12. 计算（结果用度、分表示）．13. 同一条直线上有四点，已知： ， 且 ， 则的长是 ．三、解答题（共7题，共61分）
-
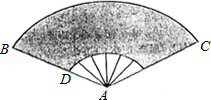
14. 如图扇形纸扇完全打开后，外侧两竹条AB、AC的夹角为120°，AB长为30cm，贴纸部分BD长为20cm，求贴纸部分的面积．
15. 如图，已知三点A、B、C．
(1)、请读下列语句，并分别画出图形①画直线AB；②画射线AC；③连接BC．
(2)、在（1）的条件下，图中共有条射线．(3)、从点C到点B的最短路径是 ， 依据是 ．16. 记长方形的长为a，宽为b(如图)．
(1)、用直尺和圆规作长与宽的差．(2)、比较a与2b的大小，并说明你是怎样比较的．17. 如图所示，点P是线段AB上任意一点，AB=12 cm，C，D两点分别从点P，B同时向点A运动，且点C的运动速度为2 cm/s，点D的运动速度为3 cm/s，运动时间为t s.
(1)、若AP=8 cm：①两点运动1 s后，求CD的长；
②当点D在线段PB上运动时，试说明：AC=2CD；
(2)、当t=2时，CD=1 cm，试探索AP的长.18. 如图，已知∠AOB＝90°，三角形COD是含有45°角的三角板，∠COD＝45°，OE平分∠BOC ．
(1)、如图1，当∠AOC＝30°时，∠DOE＝°；(2)、如图2，当∠AOC＝60°时，∠DOE＝°；(3)、如图3，当∠AOC＝α（90°＜α＜180°）时，求∠DOE的度数（用α表示）；(4)、由前三步的计算，当0°＜∠AOC＜180°时，请直接写出∠AOC与∠DOE的数量关系为 ．19. 阅读下列材料并填空：(1)、探究：平面上有n个点（n≥2）且任意3个点不在同一条直线上，经过每两点画一条直线，一共能画多少条直线？我们知道，两点确定一条直线．平面上有2个点时，可以画 =1条直线，平面内有3个点时，一共可以画 =3条直线，平面上有4个点时，一共可以画 =6条直线，平面内有5个点时，一共可以画条直线，…平面内有n个点时，一共可以画条直线．
(2)、运用：某足球比赛中有22个球队进行单循环比赛（每两队之间必须比赛一场），一共要进行多少场比赛？