人教版九年级上学期数学课时进阶测试24.4弧长及扇形面积(三阶)
试卷更新日期:2024-09-06 类型:同步测试
一、选择题
-
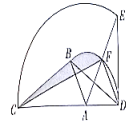
1. 如图,在扇形中,平分交于点 , 点为半径上一动点.若 , 则阴影部分周长的最小值为( )
 A、 B、 C、 D、2. 如图,在矩形中,是边上的一个动点,连结 , 点关于直线的对称点为 , 当运动时,也随之运动.若从运动到 , 则点经过的路径长是( )
A、 B、 C、 D、2. 如图,在矩形中,是边上的一个动点,连结 , 点关于直线的对称点为 , 当运动时,也随之运动.若从运动到 , 则点经过的路径长是( ) A、 B、 C、 D、3. 如图,在中, , 半径为6的与相切于点 , 与交于点 , 连接 , , , 有下列结论:①平分;②;③若 , 扇形的面积为;④若 , 则 . 其中正确的是( )
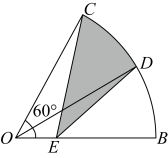
A、 B、 C、 D、3. 如图,在中, , 半径为6的与相切于点 , 与交于点 , 连接 , , , 有下列结论:①平分;②;③若 , 扇形的面积为;④若 , 则 . 其中正确的是( ) A、①③ B、②④ C、②③④ D、①②④4. 如图,在中, , , , 点为的中点,以点为圆心作圆心角为的扇形 , 点恰在弧上,则图中阴影部分的面积为( )
A、①③ B、②④ C、②③④ D、①②④4. 如图,在中, , , , 点为的中点,以点为圆心作圆心角为的扇形 , 点恰在弧上,则图中阴影部分的面积为( ) A、 B、 C、 D、5. 如图,菱形 中, , .以A为圆心, 长为半径画 ,点P为菱形内一点,连 , , .若 ,且 ,则图中阴影部分的面积为( )
A、 B、 C、 D、5. 如图,菱形 中, , .以A为圆心, 长为半径画 ,点P为菱形内一点,连 , , .若 ,且 ,则图中阴影部分的面积为( )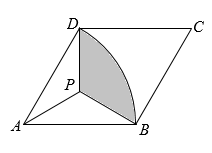 A、 B、 C、 D、6. 如图,正方形ABCD的边长为3,将长为2 的线段QF的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在AB上滑动,同时点F在BC上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段QF的中点M所经过的路线长为( )
A、 B、 C、 D、6. 如图,正方形ABCD的边长为3,将长为2 的线段QF的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在AB上滑动,同时点F在BC上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段QF的中点M所经过的路线长为( )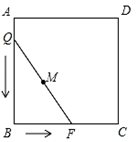 A、 B、 C、 D、7. 如图,用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则图中阴影部分面积( )
A、 B、 C、 D、7. 如图,用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则图中阴影部分面积( )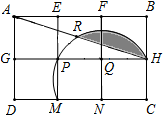 A、π﹣ B、π﹣5 C、2π﹣5 D、3π﹣2
A、π﹣ B、π﹣5 C、2π﹣5 D、3π﹣2二、填空题
-
8. 如图,在中, , 以直角边为直径作半圆交于点D,以为边作等边 , 延长交于点F, , 则图中阴影部分的面积为 . (结果不取近似值)
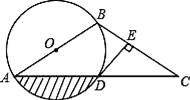
 9. 如图AB为⊙O的直径,点P为AB延长线上的点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是(写所有正确论的号)
9. 如图AB为⊙O的直径,点P为AB延长线上的点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是(写所有正确论的号)①AM平分∠CAB;② ;③若AB=4,∠APE=30°,则 的长为 ;④若AC=3BD,则有tan∠MAP= .
 10. 如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆,半圆恰好经过三角形的直角顶点C,以点D为顶点,作90°的∠EDF,与半圆交于点E,F,则图中阴影部分的面积是 .
10. 如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆,半圆恰好经过三角形的直角顶点C,以点D为顶点,作90°的∠EDF,与半圆交于点E,F,则图中阴影部分的面积是 .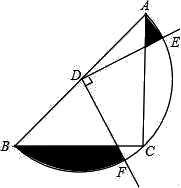 11. 如图,点0为正六边形ABCDEF的中心,点M为AF中点,以点0为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2 , 则r1:r2=
11. 如图,点0为正六边形ABCDEF的中心,点M为AF中点,以点0为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2 , 则r1:r2=
三、解答题