人教版九年级上学期数学课时进阶测试24.3正多边形和圆（三阶）

试卷更新日期：2024-09-06 类型：同步测试

进入出卷网下载

一、选择题（每题3分）

1. 如图，点A ， B ， C ， D ， E均在 $⊙ O$ 上，且 $B D$ 经过圆心O ，连接 $A B ， A E ， C E$ ，若 $∠ B + ∠ E = 150 °$ ，则弧 $C D$ 所对的圆心角的度数为（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
2. 如图，正五边形ABCDE内接于⊙O，过点A的切线与CB的延长线相交于点F，则∠F=（）

A、18° B、36° C、54° D、72°

查看试题解析
3. 已知AB是半径为1的圆O的一条弦，且AB=a＜1，以AB为一边在圆O内作正△ABC，点D为圆O上不同于点A的一点，且DB=AB=a，DC的延长线交圆O于点E，则AE的长为（）

A、 $\frac{\sqrt{5}}{2} a$ B、1 C、 $\frac{\sqrt{3}}{2}$ D、a

查看试题解析
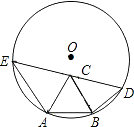4. 如图是由7个形状、大小完全相同的正六边形组成的网格，正六边形的各顶点称为格点，直角△ABC的顶点均在格点上，则满足条件的点C有（）

A、6个 B、8个 C、10个 D、12个

查看试题解析
5. 如图，已知正六边形ABCDEF中，G，H分别是AF和CD的中点，P是GH上的动点，连接AP，BP，则AP+BP的值最小时，BP与HG的夹角（锐角）度数为（）度．

A、 $45$ B、60 C、 $75$ D、 $30$

查看试题解析
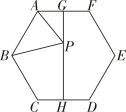6. 如图，在矩形ABCD中，AB＞AD，∠DAB的平分线与CD交于点E，过点C作CF⊥AE于点F，连接BF，DF．有下列结论：①DE＝BC；②DF＝BF；③∠CDF＝∠CBF；④B，C，D，F四点在同一个圆上．其中正确结论的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 如图， $⊙ O$ 与正六边形 $O A B C D E$ 的边 $O A 、 O E$ 分别交于点 $F 、 G$ ，点 $M$ 为劣弧 $F G$ 的中点．若 $F M = 2 \sqrt{2}$ ，则 $⊙ O$ 的半径为（）

A、2 B、 $\sqrt{6}$ C、 $2 \sqrt{2}$ D、 $2 \sqrt{6}$

查看试题解析

二、填空题（每题3分）

8. 如图，已知点D在锐角三角形ABC的BC边上，AB＞AC，点E、F分别是△ABD、△ACD的外心，且EF=BC，那么∠ADC=度．

查看试题解析
9. 如图，边长为1的正六边形 $A B C D E F$ 放置于平面直角坐标系中，边 $A B$ 在x轴正半轴上，顶点F在y轴正半轴上，将正六边形 $A B C D E F$ 绕坐标原点O顺时针旋转，每次旋转 $60 °$ ，那么经过第2022次旋转后，顶点D的坐标为．

查看试题解析
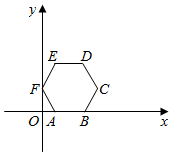10. 如图，正六边形ABCDEF的边长是6+4 $\sqrt{3}$ ，点O₁ ， O₂分别是△ABF，△CDE的内心，则O₁O₂= ．

查看试题解析
11. 如图，边长为6的正方形 $A B C D$ 内接于 $⊙ O$ ，点E是 $\overset{⌢}{A B}$ 上的一动点（不与A ， B重合，点F是 $\overset{⌢}{B C}$ 上的一点，连接 $O E ， O F$ ，分别与 $A B ， B C$ 交于点G ， H ，且 $∠ E O F = 90 °$ ，有以下结论：① $O G = O H$ ；② $△ G B H$ 周长的最小值为 $6 + 2 \sqrt{2}$ ；③随着点E位置的变化，四边形 $O G B H$ 的面积始终为9.其中正确的是.（填序号）

查看试题解析

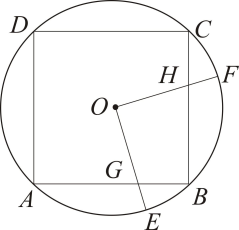
三、解答题

12. 如图，已知△ABC是⊙O的内接三角形，点P是 $\overset{⌢}{A B C}$ 的中点，过点P作PD⊥AB，交AB延长线于点D，连接BP．

(1)、求证：∠CBP＝∠PBD；

(2)、过P作PG⊥BC交BC于G点，若AB＝6，BD＝4，求BC的长．

查看试题解析
13. 研究发现：当四边形的对角线互相垂直时，该四边形的面积等于对角线乘积的一半.如图甲所示，已知四边形ABCD内接于 $⊙ O$ ，对角线 $A C = B D$ ，且AC⊥BD.

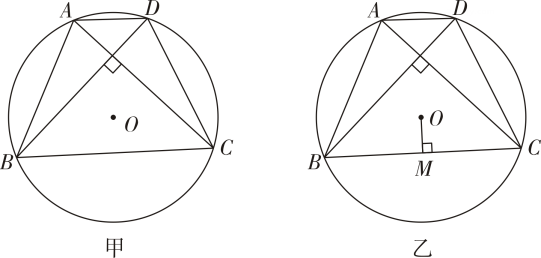(1)、求证：AB=CD.

(2)、若 $⊙ O$ 的半径为8， $\overset{⌢}{B D}$ 的度数为120°，求四边形ABCD的面积.

(3)、如图乙所示，作OM⊥BC于点M，请猜测OM与AD的数量关系并证明.

查看试题解析
14. 某数学学习小组的成员在探索“各内角都相等的圆内接多边形是否为正多边形”时，进行了如下探讨：
甲同学：我发现这种多边形不一定是正多边形.如圆内接矩形不一定是正方形.
乙同学：但是边数为3时，它是正三角形，而且我猜想，边数为5时，它应该是正五边形……
丙同学：我发现边数为6时，它也不一定是正六边形.如图甲所示， $△ A B C$ 是正三角形， $\overset{⌢}{A D} ， \overset{⌢}{B E} ， \overset{⌢}{C F}$ 均相等，很显然由此构造的六边形ADBECF并不是正六边形.

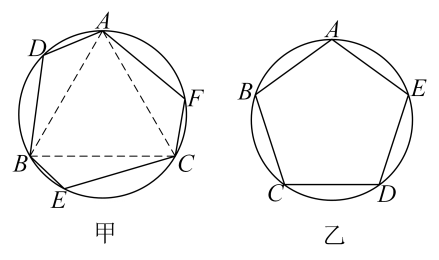(1)、如图乙所示，若圆内接五边形ABCDE的各内角均相等，则∠ABC= .请简要说明圆内接五边形ABCDE为正五边形的理由.

(2)、请证明丙同学构造的六边形各内角相等.

(3)、根据以上的探索过程，就“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n(n≥3，n为整数)”的关系，请提出你的猜想.(不需证明)

查看试题解析