人教版九年级上学期数学课时进阶测试24.3正多边形和圆(二阶)
试卷更新日期:2024-09-06 类型:同步测试
一、选择题
-
1. 如图,是正n边形纸片的一部分,其中l , m是正n边形两条边的一部分,若l , m所在的直线相交形成的锐角为 , 则n的值是( )
 A、5 B、6 C、8 D、102. 如图,△ABC圆内接于⊙O , 连接OA , OB , OC , ∠AOB=2∠BOC . 若∠OBC=65° , 则∠ABC的度数是( )
A、5 B、6 C、8 D、102. 如图,△ABC圆内接于⊙O , 连接OA , OB , OC , ∠AOB=2∠BOC . 若∠OBC=65° , 则∠ABC的度数是( ) A、95° B、105° C、115° D、135°3. 如图,在中,I为内心,P为的外接圆上一点,于点E,于点F.设 , , 若 , 则( )
A、95° B、105° C、115° D、135°3. 如图,在中,I为内心,P为的外接圆上一点,于点E,于点F.设 , , 若 , 则( ) A、 B、 C、 D、4. 如图,四边形内接于 , 连接 . 若 , , 则的度数是( )
A、 B、 C、 D、4. 如图,四边形内接于 , 连接 . 若 , , 则的度数是( ) A、125° B、130° C、135° D、140°
A、125° B、130° C、135° D、140°二、填空题
-
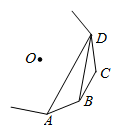
5. 如图, 、 、 、 为一个正多边形的顶点, 为正多边形的中心,若 ,则这个正多边形的边数为.
 6. 如图,四边形是的内接四边形,是的直径, , 则的度数是 .
6. 如图,四边形是的内接四边形,是的直径, , 则的度数是 . 7. 如图,在平面直角坐标系中,点在轴负半轴上,点在轴正半轴上,经过 , , , 四点, , , 则圆心点的坐标是.
7. 如图,在平面直角坐标系中,点在轴负半轴上,点在轴正半轴上,经过 , , , 四点, , , 则圆心点的坐标是.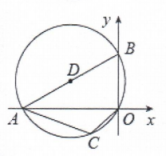 8. 如图,点O是正六边形的中心,以为边在正六边形的内部作正方形连接 , 则°.
8. 如图,点O是正六边形的中心,以为边在正六边形的内部作正方形连接 , 则°. 9. 刘徽是我国魏晋时期卓越的数学家,他首次提出“割圆术”,利用圆内接正多边形逐步逼近圆来近似计算圆周率,方法如图:作正六边形ABCDEF内接于 , 取的中点G,与交于点H;连接、;依次对剩余五段弧取中点可得一个圆内接正十二边形,记正十二边形的面积为 , 正六边形的面积为 , 则.
9. 刘徽是我国魏晋时期卓越的数学家,他首次提出“割圆术”,利用圆内接正多边形逐步逼近圆来近似计算圆周率,方法如图:作正六边形ABCDEF内接于 , 取的中点G,与交于点H;连接、;依次对剩余五段弧取中点可得一个圆内接正十二边形,记正十二边形的面积为 , 正六边形的面积为 , 则.
三、解答题

