江苏省南通市2024年中考数学试卷

试卷更新日期：2024-09-05 类型：中考真卷

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）

1. 如果零上2℃记作+2℃，那么零下3℃记作（）

A、﹣3℃ B、3℃ C、﹣5℃ D、5℃

查看试题解析
2. 2024年5月，财政部下达1582亿元资金，支持地方进一步巩固和完善城乡统一、重在农村的义务教育经费保障机制．将“1582亿”用科学记数法表示为（）

A、158.2×10⁹ B、15.82×10¹⁰ C、1.582×10¹¹ D、1.582×10¹²

查看试题解析
3. 计算 $\sqrt{27} \times \sqrt{\frac{1}{3}}$ 的结果是（）

A、9 B、3 C、3 $\sqrt{3}$ D、 $\sqrt{3}$

查看试题解析
4. 如图是一个几何体的三视图，该几何体是（）

A、球 B、棱柱 C、圆柱 D、圆锥

查看试题解析
5. 如图，直线a∥b ，矩形ABCD的顶点A在直线b上，若∠2＝41°，则∠1的度数为（）

A、41° B、51° C、49° D、59°

查看试题解析
6. 红星村种的水稻2021年平均每公顷产7200kg ， 2023年平均每公顷产8450kg ．求水稻每公顷产量的年平均增长率．设水稻每公顷产量的年平均增长率为x ，列方程为（）

A、7200（1+x）²＝8450 B、7200（1+2x）＝8450 C、8450（1﹣x）²＝7200 D、8450（1﹣2x）＝7200

查看试题解析
7. 将抛物线y＝x²+2x﹣1向右平移3个单位后得到新抛物线的顶点坐标为（）

A、（﹣4，﹣1） B、（﹣4，2） C、（2，1） D、（2，﹣2）

查看试题解析
8. “赵爽弦图”巧妙利用面积关系证明了勾股定理．如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形．设直角三角形的两条直角边长分别为m ， n（m＞n）．若小正方形面积为5，（m+n）²＝21，则大正方形面积为（）

A、12 B、13 C、14 D、15

查看试题解析
9. 甲、乙两人沿相同路线由A地到B地匀速前进，两地之间的路程为20km ．两人前进路程s（单位：km）与甲的前进时间t（单位：h）之间的对应关系如图所示．根据图象信息，下列说法正确的是（）

A、甲比乙晚出发1h B、乙全程共用2h C、乙比甲早到B地3h D、甲的速度是5km/h

查看试题解析
10. 在△ABC中，∠B＝∠C＝α（0°＜α＜45°），AH⊥BC ，垂足为H ， D是线段HC上的动点（不与点H ， C重合），将线段DH绕点D顺时针旋转2α得到线段DE ．两位同学经过深入研究，小明发现：当点E落在边AC上时，点D为HC的中点；小丽发现：连接AE ，当AE的长最小时，AH²＝AB•AE请对两位同学的发现作出评判（）

A、小明正确，小丽错误 B、小明错误，小丽正确 C、小明、小丽都正确 D、小明、小丽都错误

查看试题解析

二、填空题（本大题共8小题，第11～12题每小题3分，第13～18题每小题4分，共30分.不需写出解答过程，请把答案直接填写在答题卡相应位置上）

11. 分解因式：ax﹣ay＝．

查看试题解析
12. 已知圆锥底面半径为2cm，母线长为6cm，则该圆锥的侧面积是 cm² ．

查看试题解析
13. 已知关于x的一元二次方程x²﹣2x+k＝0有两个不相等的实数根．请写出一个满足题意的k的值：．

查看试题解析
14. 社团活动课上，九年级学习小组测量学校旗杆的高度．如图，他们在B处测得旗杆顶部A的仰角为60°，BC＝6m ，则旗杆AC的高度为 m ．

查看试题解析
15. 若菱形的周长为20cm，且有一个内角为45°，则该菱形的高为 cm．

查看试题解析
16. 已知蓄电池的电压为定值，使用蓄电池时，电流I(单位：A)与电阻R(单位： Ω)是反比例函数关系，它的图象如图所示，如果以此蓄电池为电源的用电器，其限制电流不能超过10A，那么用电器可变电阻R应控制的范围是。

查看试题解析
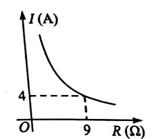17. 如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝5．正方形DEFG的边长为 $\sqrt{5}$ ，它的顶点D ， E ， G分别在△ABC的边上，则BG的长为．

查看试题解析
18. 平面直角坐标系xOy中，已知A（3，0），B（0，3）．直线y＝kx+b（k ， b为常数，且k＞0）经过点（1，0），并把△AOB分成两部分，其中靠近原点部分的面积为 $\frac{15}{4}$ ，则k的值为．

查看试题解析

三、解答题（本大题共8小题，共90分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）

19.

(1)、计算：2m（ $\frac{1}{2}$ m﹣1）﹣m（m+1）；

(2)、解方程 $\frac{x}{x + 1} -$ 1 $= \frac{2 x}{3 x + 3}$ ．

查看试题解析
20. 我国淡水资源相对缺乏，节约用水应成为人们的共识．为了解某小区家庭用水情况，随机调查了该小区50个家庭去年的月均用水量（单位：吨），绘制出如下未完成的统计图表．
50个家庭去年月均用水量频数分布表
组别
家庭月均用水量（单位：吨）
频数
A
2.0≤t＜3.4
7
B
3.4≤t＜4.8
m
C
4.8≤t＜6.2
n
D
6.2≤t＜7.6
6
E
7.6≤t＜9.0
2
合计

50
根据上述信息，解答下列问题：

(1)、m＝， n＝；

(2)、这50个家庭去年月均用水量的中位数落在组；

(3)、若该小区有1200个家庭，估计去年月均用水量小于4.8吨的家庭数有多少个？

查看试题解析
21. 如图，点D在△ABC的边AB上，DF经过边AC的中点E ，且EF＝DE ．求证：CF∥AB ．

查看试题解析
22. 南通地铁1号线“世纪大道站”有标识为1、2、3、4的四个出入口．某周六上午，甲、乙两位学生志愿者随机选择该站一个出入口，开展志愿服务活动．

(1)、甲在2号出入口开展志愿服务活动的概率为；

(2)、求甲、乙两人在同一出入口开展志愿服务活动的概率．

查看试题解析
23. 如图，△ABC中，AB＝3，AC＝4，BC＝5，⊙A与BC相切于点D ．

(1)、求图中阴影部分的面积；

(2)、设⊙A上有一动点P ，连接CP ， BP ．当CP的长最大时，求BP的长．

查看试题解析
24. 某快递企业为提高工作效率，拟购买A、B两种型号智能机器人进行快递分拣．相关信息如下：
信息一
A型机器人台数
B型机器人台数
总费用（单位：万元）
1
3
260
3
2
360
信息二
A型机器人每台每天可分拣快递22万件；
B型机器人每台每天可分拣快递18万件．

(1)、求A、B两种型号智能机器人的单价；

(2)、现该企业准备用不超过700万元购买A、B两种型号智能机器人共10台．则该企业选择哪种购买方案，能使每天分拣快递的件数最多？

查看试题解析
25. 已知函数y＝（x﹣a）²+（x﹣b）²（a ， b为常数）．设自变量x取x₀时，y取得最小值．

(1)、若a＝﹣1，b＝3，求x₀的值；

(2)、在平面直角坐标系xOy中，点P（a ， b）在双曲线y $= - \frac{2}{x}$ 上，且x₀ $= \frac{1}{2}$ ．求点P到y轴的距离；

(3)、当a²﹣2a﹣2b+3＝0，且1≤x₀＜3时，分析并确定整数a的个数．

查看试题解析
26. 综合与实践：九年级某学习小组围绕“三角形的角平分线”开展主题学习活动．

(1)、【特例探究】
如图①，②，③是三个等腰三角形（相关条件见图中标注），列表分析两腰之和与两腰之积．
等腰三角形两腰之和与两腰之积分析表
图序
角平分线AD的长
∠BAD的度数
腰长
两腰之和
两腰之积
图①
1
60°
2
4
4
图②
1
45°
$\sqrt{2}$
$2 \sqrt{2}$
2
图③
1
30°
    ▲
    ▲
    ▲
请补全表格中数据，并完成以下猜想．
已知△ABC的角平分线AD＝1，AB＝AC ， ∠BAD＝α，用含α的等式写出两腰之和AB+AC与两腰之积AB•AC之间的数量关系：        ▲         ．

(2)、【变式思考】
已知△ABC的角平分线AD＝1，∠BAC＝60°，用等式写出两边之和AB+AC与两边之积AB•AC之间的数量关系，并证明．

(3)、【拓展运用】
如图④，△ABC中，AB＝AC＝1，点D在边AC上，BD＝BC＝AD ．以点C为圆心，CD长为半径作弧与线段BD相交于点E ，过点E作任意直线与边AB ， BC分别交于M ， N两点．请补全图形，并分析 $\frac{1}{B M} + \frac{1}{B N}$ 的值是否变化？

查看试题解析

组别	家庭月均用水量（单位：吨）	频数
A	2.0≤t＜3.4	7
B	3.4≤t＜4.8	m
C	4.8≤t＜6.2	n
D	6.2≤t＜7.6	6
E	7.6≤t＜9.0	2
合计		50

A型机器人台数	B型机器人台数	总费用（单位：万元）
1	3	260
3	2	360

图序	角平分线AD的长	∠BAD的度数	腰长	两腰之和	两腰之积
图①	1	60°	2	4	4
图②	1	45°	$\sqrt{2}$	$2 \sqrt{2}$	2
图③	1	30°	▲	▲	▲