人教版九年级上学期数学课时进阶测试24.1圆有关的性质(三阶)
试卷更新日期:2024-09-04 类型:同步测试
一、选择题(每题3分)
-
1. 如图,AB是⊙O的直径,点C , 点D是半圆上两点,连结AC , BD相交于点P , 连结AD , OD . 已知OD⊥AC于点E , AB=2.下列结论:
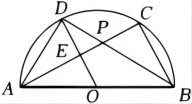
①∠DBC+∠ADO=90°;②AD2+AC2=4;③若AC=BD , 则DE=OE;④若点P为BD的中点,则DE=2OE .
其中正确的是( )
A、①②③ B、①③④ C、②③④ D、①②④2. 如图,C是以为直径的半圆O上一点,连接 , , 分别以 , 为直径向外作半圆, , 的中点分别为D,E,连接 , , 若要求出的长,只需知道( ) A、的长 B、的长 C、的长 D、的长3. 如图,抛物线y=x2﹣8x+15与x轴交于A、B两点,对称轴与x轴交于点C , 点D(0,﹣2),点E(0,﹣6),点P是平面内一动点,且满足∠DPE=90°,M是线段PB的中点,连接CM . 则线段CM的最大值是( )
A、的长 B、的长 C、的长 D、的长3. 如图,抛物线y=x2﹣8x+15与x轴交于A、B两点,对称轴与x轴交于点C , 点D(0,﹣2),点E(0,﹣6),点P是平面内一动点,且满足∠DPE=90°,M是线段PB的中点,连接CM . 则线段CM的最大值是( ) A、3 B、 C、 D、5
A、3 B、 C、 D、5二、填空题(每题3分)
-
4. 如图,∠BAC=60°,∠ABC=45°,AB= , D是线段BC上的一个动点,以AD为直径画⊙O分别交AB , AC于E , F , 连接EF , 则线段EF长度的最小值为 .
 5. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为底边向外作高为AC,BC长的等腰三角形ACM,等腰三角形BCN, , 的中点分别是P,Q.若MP+NQ=12,AC+BC=15,则AO的长是.
5. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为底边向外作高为AC,BC长的等腰三角形ACM,等腰三角形BCN, , 的中点分别是P,Q.若MP+NQ=12,AC+BC=15,则AO的长是. 6. 如图, 等腰内接于 , , , 点D是上一点, 连接 , 点E是上一点,满足. 若 , 则的面积是.
6. 如图, 等腰内接于 , , , 点D是上一点, 连接 , 点E是上一点,满足. 若 , 则的面积是.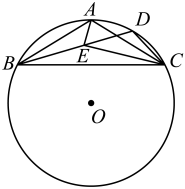
三、解答题
-
7. 如图,AB是⊙O的直径,AB=4,点E为弧AC的中点,连结AC,BE交于点D,过点A作AF⊥AB交BE的延长线于点F,AF=3.
 (1)、求证:AD=AF;(2)、求△ABD的周长;(3)、若点P为⊙O上一点,当△AEP为等腰三角形时,求AP的长.8. 综合与实践:
(1)、求证:AD=AF;(2)、求△ABD的周长;(3)、若点P为⊙O上一点,当△AEP为等腰三角形时,求AP的长.8. 综合与实践:“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.
提出问题:
如图1所示,在线段同侧有两点 , , 连接 , , , , 如果 , 那么 , , , 四点在同一个圆上.

探究展示:
如图2所示,作经过点 , , 的 , 在劣弧上取一点(不与 , 重合),连接 , ,

则 , (依据
,
,
点 , , , 四点在同一个圆上,(对角互补的四边形四个顶点共圆)
点 , 在点 , , 所确定的上,(依据
点 , , , 四点在同一个圆上;
反思归纳:
(1)上述探究过程中的“依据1”、“依据2”分别是指什么?
依据1:______;(从右边框内选一个选项,直接填序号)
依据2:______.(从右边框内选一个选项,直接填序号)
①圆内接四边形对角互补;
②对角互补的四边形四个顶点共圆;
③过不在同一直线上的三个点有且只有一个圆;
④经过两点的圆的圆心在这两点所连线段的垂直平分线上;
(2)如图3所示,在四边形中, , , 则的度数为______.
