人教版九年级上学期数学第二十三章质量检测(高阶)
试卷更新日期:2024-09-03 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,将含有角的直角三角板放置在平面直角坐标系中,在x轴上,若 , 将三角板绕原点O顺时针旋转 , 则点A的对应点的坐标为( )
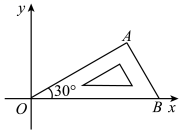 A、 B、 C、 D、2. 如图,平行四边形中, , , , 是边上一点,且 , 是边上的一个动点,将线段绕点顺时针旋转 , 得到 , 连接、 , 则的最小值是( )
A、 B、 C、 D、2. 如图,平行四边形中, , , , 是边上一点,且 , 是边上的一个动点,将线段绕点顺时针旋转 , 得到 , 连接、 , 则的最小值是( ) A、 B、 C、14 D、3. 如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB , 将线段BM绕点B逆时针旋转60°得到BN , 连结HN . 则在点M运动过程中,线段HN长度的最小值是( )
A、 B、 C、14 D、3. 如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB , 将线段BM绕点B逆时针旋转60°得到BN , 连结HN . 则在点M运动过程中,线段HN长度的最小值是( ) A、6 B、3 C、2 D、1.54. 如图,在平面直角坐标系中,Rt△AOB的一条直角边OB在x轴上,点A的坐标为(-6,4);Rt△COD中,∠COD=90°,OD=4 , ∠D=30°,连接BC,点M是BC中点,连接AM.将Rt△COD以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是( )
A、6 B、3 C、2 D、1.54. 如图,在平面直角坐标系中,Rt△AOB的一条直角边OB在x轴上,点A的坐标为(-6,4);Rt△COD中,∠COD=90°,OD=4 , ∠D=30°,连接BC,点M是BC中点,连接AM.将Rt△COD以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是( )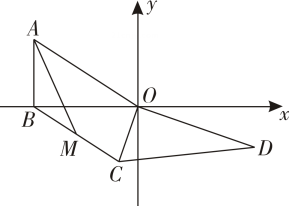 A、3 B、6-4 C、2-2 D、25. 如图,已知在平面直角坐标系中,一段抛物线 , 记为抛物线 , 它与轴交于点 , ;将抛物线绕点旋转得抛物线 , 交轴于点 , ;将抛物线绕点 , 旋转得抛物线 , 交轴于点 , ;……如此进行下去,得到一条“波浪线”,若点在此“波浪线”上,则的值为( )
A、3 B、6-4 C、2-2 D、25. 如图,已知在平面直角坐标系中,一段抛物线 , 记为抛物线 , 它与轴交于点 , ;将抛物线绕点旋转得抛物线 , 交轴于点 , ;将抛物线绕点 , 旋转得抛物线 , 交轴于点 , ;……如此进行下去,得到一条“波浪线”,若点在此“波浪线”上,则的值为( ) A、 B、 C、9 D、5
A、 B、 C、9 D、5二、填空题(每题3分,共15分)
-
6. 如图,已知△ABC , ∠ABC<60°,将△ABC绕点A逆时针旋转60°得到△ADE , DE与BC交于点P . 下列结论:
①∠EPC=60°;
②AC与DE互相平分;
③PA+PC=PE;
④PA平分∠BPE , 其中正确结论的是 .
 7. 如图,正方形中, , O是边的中点,点E是正方形内一动点, , 连接 , 将线段绕点D逆时针旋转得 , 连接 , 则线段长的最小值为 .
7. 如图,正方形中, , O是边的中点,点E是正方形内一动点, , 连接 , 将线段绕点D逆时针旋转得 , 连接 , 则线段长的最小值为 . 8. 如图,“心”形是由抛物线 和它绕着原点O , 顺时针旋转60°的图形经过取舍而成的,其中顶点C的对应点为D , 点A , B是两条抛物线的两个交点,点E , F , G是抛物线与坐标轴的交点,则AB= .
8. 如图,“心”形是由抛物线 和它绕着原点O , 顺时针旋转60°的图形经过取舍而成的,其中顶点C的对应点为D , 点A , B是两条抛物线的两个交点,点E , F , G是抛物线与坐标轴的交点,则AB= .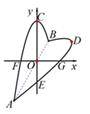
三、作图题(共2题,共18分)
-
9. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
 (1)、请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(1)、请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)、请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)、在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
四、解答题(共5题,共45分)
-
10. 如图,在矩形中, , , , 垂足为E . F是点E关于的对称点,连接 .
 (1)、求证:;(2)、求和的长;(3)、将一个与完全重合的透明三角板沿射线方向平移.
(1)、求证:;(2)、求和的长;(3)、将一个与完全重合的透明三角板沿射线方向平移.①设点在上移动的距离是m . 当点分别落在线段上时,求相应的m的值;
②当点落在上时,立刻将绕点顺时针旋转,且旋转60°时停止.点H在上,且 . 若平移的速度为每秒1个单位长度,绕点旋转的速度为每秒5°,在整个运动过程中,直接写出点H在区域(含边界)内的时长.
11. 如图,已知抛物线()与轴交于点和点 , 与轴交于点 , 且 . (1)、求此抛物线的解析式;(2)、若点为第二象限抛物线上一动点,连接 , , 求四边形面积的最大值,并求出此时点的坐标;(3)、点在抛物线的对称轴上,若线段绕点逆时针旋转90°后,点的对应点恰好也落在此抛物线上,求点的坐标.12. 如图,中, , 将绕点A逆时针旋转得到 , 与交于点D , 与交于点E , 与交于点F , 当B、D、F重合时停止旋转.
(1)、求此抛物线的解析式;(2)、若点为第二象限抛物线上一动点,连接 , , 求四边形面积的最大值,并求出此时点的坐标;(3)、点在抛物线的对称轴上,若线段绕点逆时针旋转90°后,点的对应点恰好也落在此抛物线上,求点的坐标.12. 如图,中, , 将绕点A逆时针旋转得到 , 与交于点D , 与交于点E , 与交于点F , 当B、D、F重合时停止旋转. (1)、证明:在旋转过程中;(2)、如图1,当平分时,证明:;(3)、如图2,若 , , 在旋转过程中,当是等腰三角形时,求该等腰三角形底边的长度.
(1)、证明:在旋转过程中;(2)、如图1,当平分时,证明:;(3)、如图2,若 , , 在旋转过程中,当是等腰三角形时,求该等腰三角形底边的长度.五、实践探究题(共12分)
-
13. 问题解决
一节数学课上,老师提出了这样一个问题:如图①,点P是等边内的一点, , , .你能求出的度数和等边的面积吗?小明通过观察、分析、思考,形成了如下思路:

如图①将绕点B逆时针旋转 , 得到 , 连接 , 可得是等边三角形,根据勾股定理逆定理可得是直角三角形,从而使问题得到解决.
(1)、结合小明的思路完成填空: , , , .(2)、类比探究①.如图②,若点P是正方形内一点, , , , 求的度数和正方形的面积.
②.如图③,若点P是正方形外一点, , , , 求的度数和正方形的面积.
-