广东省惠州市博罗县2023-2024学年九年级上学期期末考试数学试题

试卷更新日期：2024-09-02 类型：期末考试

进入出卷网下载

一、选择题：(本大题共10小题，每小题3分，共30分)．

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列是一元二次方程的为（）

A、 $x - 2 y + 1 = 0$ B、 $x^{2} - 2 x - 3 = 0$ C、 $2 x + 3 = 0$ D、 $x^{2} + 2 y - 10 = 0$

查看试题解析
3. 毛泽东在《沁园春•雪》中提到五位历史名人：秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗，小红将这五位名人简介分别写在五张完全相同的知识卡片上，小哲从中随机抽取一张，卡片上介绍的人物是唐朝以后出生的概率是（　　）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
4. 关于反比例函数y= $- \frac{2}{x}$ ，下列说法正确的是（）

A、图象过点(1，2) B、图象在第一、三象限 C、当 $x$ ＞0时，y随 $x$ 的增大而减小 D、当 $x$ ＜0时，y随 $x$ 的增大而增大

查看试题解析
5. 如图，在半径为 $5 c m$ 的⊙ $O$ 中，弦 $A B = 6 c m$ ， $O C ⊥ A B$ 于点 $C$ ，则OC长为（）

A、 $3 c m$ B、 $4 c m$ C、 $5 c m$ D、 $6 c m$

查看试题解析
6. 若 $x_{1} ， x_{2}$ 是一元二次方程 $x^{2} - 5 x + 6 = 0$ 的两个根，则 $x_{1} + x_{2}$ 的值是（）

A、 $1$ B、 $- 5$ C、 $5$ D、 $6$

查看试题解析
7. 将抛物线y＝4x²先向右平移3个单位，再向下平移5个单位，得到的抛物线解析式（　　）

A、y＝4(x+3)²+5 B、y＝4(x+3)²﹣5 C、y＝4(x﹣3)²+5 D、y＝4(x﹣3)²﹣5

查看试题解析
8. 如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠C的度数为（）

A、32° B、42° C、58° D、116°

查看试题解析
9. △DEF和△ABC是位似图形，点O是位似中心，点D，E，F分别是OA，OB，OC的中点，若△DEF的面积是2，则△ABC的面积是（）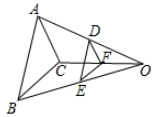

A、2 B、4 C、6 D、8

查看试题解析
10. 抛物线 $y = a x_{}^{2} + b x + c$ 的顶点为D（﹣1，2），与 $x$ 轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，其部分图象如图，则以下结论：①b²﹣4ac＜0；②当 $x$ ＞﹣1时， $y$ 随 $x$ 增大而减小；③a+b+c＜0；④若方程 $a x^{2} + b x + c$ ﹣m=0没有实数根，则m＞2；⑤3a+c＜0．其中正确结论的个数是（　　）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题：（本大题共5小题，每小题3分，共15分）.

11. 点A（3，-1）关于原点对称的点的坐标为.

查看试题解析
12. 如图，将△ABC绕点C顺时针方向旋转40°得△A^'B^'C，若AC⊥A^'B^' ，则∠A=.

查看试题解析
13. 二次函数 $y = x_{}^{2} - 2 x + 4$ 的图象的顶点坐标是.

查看试题解析
14.
如图，直线AD∥BE∥CF，BC= $\frac{1}{3}$ AC，DE=4，那么EF的值是．

查看试题解析
15. 如图，∠AOB＝90°，∠B＝30°，以点O为圆心，OA为半径作弧交AB于点A、C，交OB于点D，若OA＝3，则阴影部分的面积为.

查看试题解析

三、解答题（一）：（本大题共3小题，第16题10分，第17、18题各7分，共24分．）

16.

(1)、解方程： $x^{2} - 4 x + 3 = 0$ .

(2)、如图，△ABC三个顶点的坐标分别为A（2，4），B（1，1），C（4，3）.请画出△ABC绕点O逆时针旋转90°后的△A₁B₁C₁ ，并求出C点旋转到C₁点所经过的路径长.（结果保留π）

查看试题解析
17. 在一幅长为80cm，宽为50cm的矩形风景画的四周镶一条相同宽度金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是5400cm² ，求金色纸边的宽.

查看试题解析
18. 已知关于x的方程3x²－(k+3)x+k＝0.

(1)、求证：方程总有两个实数根；

(2)、若该方程有一个根大于2，求k的取值范围.

查看试题解析

四、解答题（二）：（本大题共3小题，每小题9分，共27分．）

19. 在一个不透明的盒子里，装有四个分别标有数字1，2，3，4的小球，它们的形状、大小、质地等完全相同，小明先从盒子里随机取出一个小球，记下数字为 $x$ ，放回盒子摇匀后，再由小华随机取出一个小球，记下数字为y.

(1)、用列表法或画树状图表示出（ $x$ ， y）的所有可能出现的结果；

(2)、求小明、小华各取一次小球所确定的点（ $x$ ， y）落在二次函数y= $x$ ²的图象上的概率.

查看试题解析
20. 综合与实践
一次数学综合实践活动课上，小华发现并证明了关于三角形角平分线的一个结论．如图1，已知AD是△ABC的角平分线，可证 $\frac{A B}{A C} = \frac{B D}{C D}$ ．小华的证明思路是：如图2，过点C作CE∥AB ，交AD的延长线于点E ，构造相似三角形来证明 $\frac{A B}{A C} = \frac{B D}{C D}$

(1)、尝试证明：请参照小华提供的思路，利用图2证明： $\frac{A B}{A C} = \frac{B D}{C D}$ ；

(2)、应用拓展：如图3，在Rt△ABC中，∠BAC＝90°，D是边BC上一点．连接AD ，将△ACD沿AD所在直线折叠，点C恰好落在边AB上的E点处．若AC＝1，AB＝2，求DE的长.

查看试题解析
21. 如图，在矩形OABC中，OA＝3，OC＝2，F是AB上的一个动点(F不与A ， B重合)，过点F的反比例函数 $y ＝ \frac{k}{x}$ (x＞0)的图象与BC边交于点E.

(1)、当F为AB的中点时，求该反比例函数的解析式和点E的坐标；

(2)、设(1)中的直线EF的解析式为y＝ax＋b ，直接写出不等式ax＋b＜ $\frac{k}{x}$ 的解集；

(3)、当k为何值时，△AEF的面积最大，最大面积是多少？

查看试题解析

五、解答题（三）：（本大题共2小题，每小题12分，共24分．）

22. 综合探究
如图，平行四边形ABCD中，AC＝BC，过A、B、C三点的⊙O与AD相交于点E，连接CE.

(1)、求证：AB＝CE；

(2)、求证：DC与⊙O相切；

(3)、若⊙O半径r＝5，AB＝8，求AE的值.

查看试题解析
23. 综合运用
如图，抛物线 $y = a x^{2} + b x - 6$ 与x轴交于A（﹣6，0），B（2，0）两点（点A在点B的左侧），与y轴交于点C，连接AC，BC.

(1)、求抛物线的函数表达式.

(2)、点P是直线AC下方抛物线上的一个动点，过点P作BC的平行线l ，交线段AC于点D ．
①试探究：在直线l上是否存在点E ，使得以点D ， C ， B ， E为顶点的四边形为菱形，若存在，求出点E的坐标，若不存在，请说明理由；
②设抛物线的对称轴与直线l交于点M ，与直线AC交于点N ．当S_△_DMN＝S_△_AOC时，请直接写出DM的长.

查看试题解析