【培优卷】湘教版（2024）七年级上册1.7 有理数的混合运算同步练习

试卷更新日期：2024-09-01 类型：同步测试

进入出卷网下载

一、选择题

1. 下面是一个“数值转换机”的示意图.若 $x = 4$ ，则输出结果为（）

A、-80 B、-75 C、85 D、-85

查看试题解析
2. 2023减去它的 $\frac{1}{2}$ ，再减去余下的 $\frac{1}{3}$ ，再减去余下的 $\frac{1}{4}$ ……依次类推，一直减到余下的 $\frac{1}{2023}$ ，则最后剩下的数是（）

A、0 B、1 C、 $\frac{2022}{2023}$ D、 $\frac{2023}{2022}$

查看试题解析
3. $\frac{(- 1)^{n} - (- 1)^{n + 1}}{2}$ （ $n$ 为正整数）的值为（）

A、 $- 1$ 或0 B、0或1 C、 $- 1$ 或1 D、 $- 1$ 或0或1

查看试题解析
4. 取一个整数，若它是奇数，则乘以3加上1，若它是偶数，则除以2，按此规则经过若干步的计算最终可得到1．这个结论在数学上还没有得到证明．但举例验证都是正确的．例如：取自然数5．经过下面5步运算可得1，即：如图所示．如果自然数m恰好经过8步运算可得到1，则所有符合条件的m的值有（）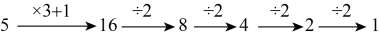

A、3个 B、4个 C、5个 D、6个

查看试题解析
5. “算24点”的游戏规则是：用“ $+$ ， $-$ ， $\times$ ， $\div$ ”…四种运算符号把给出的4个数字连接起来进行计算，要求最终算出的结果是24，例如，给出2，2，2，8这四个数，可以列式 $(2 \div 2 + 2) \times 8 = 24$ ．以下的4个数用“ $+$ ， $-$ ， $\times$ ， $\div$ ”四种运算符号不能算出结果为24的是（）

A、1，6，8，7 B、1，2，3，4 C、4，4，10，10 D、6，3，3，8

查看试题解析

6. 法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”是一样的，后面的就改用手势了.下面两个图框是用法国“小九九”计算

7 \times 8

和

8 \times 9

的两个示例，且左手伸出的手指数不大于右手伸出的手指数.若用法国的“小九九”计算

7 \times 9

，左、右手依次伸出手指的个数是（）

$7 \times 8 =$ ？

因为两手伸出的手指数的和为 $5$ ，未伸出的手指数的积为 $6$ ，所以 $7 \times 8 = 56.7 \times 8 = 10 \times (2 + 3) + 3 \times 2 = 56$

$8 \times 9 =$ ？

因为两手伸出的手指数的和为 $7$ ，未伸出的手指数的积为 $2$ ，所以 $8 \times 9 = 72.8 \times 9 = 10 \times (3 + 4) + 2 \times 1 = 72$

A、

2

，

4

B、

1

，

4

C、

3

，

4

D、

3

，

1

查看试题解析

7. 济青高铁北线，共设有11个不同站点，要保证每两个站点之间都有高铁可乘，需要印制不同的火车票（）

A、110种 B、132种 C、55种 D、66种

查看试题解析
8. 如图，已知正方形的边长为24厘米，甲，乙两动点分别从正方形ABCD的顶点D，B同时沿正方形的边开始移动，甲点按顺时针方向环行，乙点按逆时针方向环行，若乙的速度为9厘米/秒，甲的速度为3厘米/秒，当它们运动了2022秒时，它们在正方形边上相遇了（）

A、252 次 B、253次 C、254次 D、255次

查看试题解析

9. 计算机中常用的十六进制是逢16进1的计数制，采用数字0~9和字母A~F共16个计数符号，这些符号与十进制的数的对应关系如下表：

十六进制	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
十进制	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

例如，十进制中 $26 = 16 + 10$ ，用十六进制表示为1A：用十六进制表示： $D + F = 1 C$ ， $19 - F = A$ ，则 $A \times E$ ，用 $A \times E$ 十六进制可表示为（）

A、8C B、140 C、32 D、EO

查看试题解析

10. 求 $1 + 2 + 2^{2} + 2^{3} + ⋯ + 2^{2021}$ 的值，可令 $S = 1 + 2 + 2^{2} + 2^{3} + ⋯ + 2^{2021}$ ，则 $2 S = 2 + 2^{2} + 2^{3} + 2^{4} + ⋯ + 2^{2022}$ ，因此 $2 S - S = 2^{2022} - 1$ ．
仿照以上推理，计算出 $1 + 2021 + 202 1^{2} + 202 1^{3} + ⋯ + 202 1^{2021}$ 的值为（）．

A、 $\frac{202 1^{2022} - 1}{2020}$ B、 $\frac{202 1^{2021} - 1}{2020}$ C、 $\frac{202 1^{2022} - 1}{2021}$ D、 $\frac{202 1^{2022} - 1}{2022}$

查看试题解析

二、填空题

11. 如果规定符号“*”的意义是 $a * b = \frac{a \cdot b}{a + b}$ ，则2*(-3)*4的值是．

查看试题解析
12. 计算 $(\frac{1}{3} + \frac{1}{4} + \frac{1}{5}) - 2 \times (\frac{1}{2} - \frac{1}{3} - \frac{1}{4} - \frac{1}{5}) - 3 \times (\frac{1}{3} + \frac{1}{4} + \frac{1}{5} - \frac{1}{6})$ 的结果是．

查看试题解析
13. 已知整数 $a$ ， $b$ ， $c$ ， $d$ 满足 $a b c d = 6$ ，且 $a > b > c > d$ ，则 ${(a + 3 c)}^{2020} - {(3 b + d)}^{2021}$ 的值为.

查看试题解析
14. 在某次晚会上，主持人请观众心想一个数，并将这个数按右图步骤操作.

(1)、嘉嘉心想的数是-5，按照步骤操作结果是；

(2)、琪琪心想了一个数，并按步骤计算后为2024，则琪琪心想的数是.

查看试题解析

三、计算题

15.

(1)、计算： $5 - (- 2) + | - 3 | + (- 8)$ ；

(2)、 $(- 2) \times (- 3) + 12 \div \frac{1}{4} + (- 2)^{3} \times \frac{1}{8}$ ．

查看试题解析
16. 计算：

(1)、 $18 + 32 \div {(- 2)}_{}^{3} - {(- 4)}_{}^{2} \times 5$

(2)、 $(\frac{7}{9} - \frac{7}{3}) \times {(- 3)}_{}^{2} + | - \frac{1}{3} | \div (- \frac{1}{3})$

查看试题解析
17. 计算：

(1)、 $(- \frac{1}{2}) + (\frac{1}{3} + \frac{2}{3}) + (- \frac{1}{4} - \frac{2}{4} - \frac{3}{4}) + (\frac{1}{5} + \frac{2}{5} + \frac{3}{5} + \frac{4}{5}) + . . . + (\frac{1}{55} + \frac{2}{55} + . . . + \frac{54}{55})$

(2)、 $1 \frac{1}{2} - 2 \frac{5}{6} + 3 \frac{1}{12} - 4 \frac{19}{20} + 5 \frac{1}{30} - 6 \frac{41}{42} + 7 \frac{1}{56}$

查看试题解析

四、解答题

18. 小林在学习完有理数除法运算后，对算式 $(1 \frac{3}{4} - \frac{7}{8} - \frac{7}{12}) \div (- \frac{7}{8}) + (- 2) \div \frac{3}{4}$ 的计算过程如下：
解：原式 $= (1 \frac{3}{4} - \frac{7}{8} - \frac{7}{12}) \times (- \frac{8}{7}) + (- 2) \times \frac{4}{3}$                 ①
$= \frac{7}{4} \times (- \frac{8}{7}) - \frac{7}{8} \times (- \frac{8}{7}) - \frac{7}{12} \times (- \frac{8}{7}) + (- 2) \times \frac{4}{3}$         ②
$= - 2 - 1 - \frac{2}{3} - \frac{8}{3}$                         ③
$= - 6 \frac{1}{3}$ .
根据小林的计算过程回答下列问题：

(1)、小林在进行第②步运算时，运用了乘法的律；

(2)、小林的运算出现了错误，错在第（只填写序号）步；

(3)、请给出正确解法.

查看试题解析
19. 阅读材料：求1+2+2²+2³+……+2¹⁰⁰的值.
解：设S=1+2+2²+2³+……+2¹⁰⁰
将等式两边同时乘以2得
2S=2+2²+2³+2⁴……+2¹⁰¹
因此2S-S=（2+2²+2³+2⁴……+2¹⁰¹） - （1+2+2²+2³+……+2¹⁰⁰） =2¹⁰¹-1
所以S=2¹⁰¹-1
即1+2+2²+2³+……+2¹⁰⁰=2¹⁰¹-1
请你仿照此法计算：

(1)、1+2+2²+2³+2⁴+2⁵=

(2)、求1+3+3²+……+3¹⁰¹的值.

查看试题解析
20. 请你仔细阅读下列材料：计算 $\frac{1}{12} \div (\frac{1}{3} - \frac{1}{4} + \frac{1}{12})$ ．
解法一：原式＝ $\frac{1}{12} \div \frac{1}{3} - \frac{1}{12} \div \frac{1}{4} + \frac{1}{12} \div \frac{1}{12} = \frac{1}{12} \times 3 - \frac{1}{12} \times 4 + \frac{1}{12} \times 12 = \frac{1}{4} - \frac{1}{3} + 1 = \frac{11}{12}$
解法二：原式＝ $\frac{1}{12} \div (\frac{1}{3} - \frac{1}{4} + \frac{1}{12}) = \frac{1}{12} \div \frac{1}{6} = \frac{1}{12} \times 6 = \frac{1}{2}$
解法三：原式的倒数为 $(\frac{1}{3} - \frac{1}{4} + \frac{1}{12}) \div \frac{1}{12} = (\frac{1}{3} - \frac{1}{4} + \frac{1}{12}) \times 12 = \frac{1}{3} \times 12 - \frac{1}{4} \times 12 + \frac{1}{12} \times 12$ ＝4﹣3+1＝2，故原式 $= \frac{1}{2}$ ．

(1)、上述得出的结果不同，肯定有错误的解法，你认为解法是错误的．

(2)、请你选择合适的解法解答下列问题，计算： $(- \frac{1}{30}) \div (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5})$ ．

查看试题解析
21. 如图，已知数轴上有 $A$ ， $B$ 两点，分别代表 $- 40$ ， 20，两只电子蚂蚁甲，乙分别从 $A$ ， $B$ 两点同时出发，甲沿线段 $A B$ 以1个单位长度秒的速度向右运动，到达点 $B$ 处时运动停止；乙沿 $B A$ 方向以4个单位长度秒的速度向左运动．

(1)、 $A$ ， $B$ 两点间的距离为个单位长度；乙到达 $A$ 点时共运动了秒．

(2)、甲，乙在数轴上的哪个点相遇？

(3)、多少秒时，甲、乙相距10个单位长度？

(4)、若乙到达 $A$ 点后立刻掉头并保持速度不变，则甲到达 $B$ 点前，甲，乙还能在数轴上相遇吗？若能，求出相遇点所对应的数；若不能，请说明理由．

查看试题解析
22. 有一种“24点”的扑克牌游戏规则是：任抽四张牌，用各张牌上的数和加、减、乘、除四则运算(可用括号)列一个算式，先得计算结果为“24”者获胜(J，Q，K分别表示11，12，13，A表示1)．小明、小聪两人抽到的四张牌如图所示，这两组牌都能算出“24点”吗？为什么？如果算式中允许包含乘方运算，你能列出符合要求的不同的算式吗？

查看试题解析
23. 为了加强公民的节水意识，合理利用水资源，某市采用价格调控手段以达到节水的目的．如下所示是该市自来水收费价目表．
价目表
每月用水量
单价
不超出 $6 m^{3}$ 的部分
3元/ $m^{3}$
超出 $6 m^{3}$ 但不超出 $10 m^{3}$ 的部分
5元/ $m^{3}$
超出 $10 m^{3}$ 的部分
9元/ $m^{3}$
注：水费按月结算．

(1)、填空：若该户居民2月份用水 $4 m^{3}$ ，则应收水费元；

(2)、若该户居民3月份用水 $a m^{3}$ （其中 $6 < a < 10$ ），则应收水费多少元？（用 $a$ 的整式表示并化简）

(3)、若该户居民4，5月份共用水 $15 m^{3}$ （5月份用水量超过了4月份），设4月份用水 $x m^{3}$ ，求该户居民4，5月份共交水费多少元？（用 $x$ 的整式表示并化简）

查看试题解析
24. 小明的妈妈在某玩具厂工作，厂里规定每个工人每周要生产某种玩具210个，平均每天生产30个，但由于种种原因，实际每天生产量与计划量相比有出入．下表是小明妈妈某周的生产情况（超产记为正、减产记为负）：
星期
一
二
三
四
五
六
日
增减产值
＋10
－12
－4
＋8
－1
＋6
0

(1)、根据记录的数据可知小明妈妈星期三生产玩具个；

(2)、根据记录的数据可知小明妈妈本周实际生产玩具个；

(3)、该厂实行“每日计件工资制”．每生产一个玩具可得工资5元，若超额完成任务，则超过部分每个另奖3元；少生产一个则倒扣2元，那么小明妈妈这一周的工资总额是多少元？

(4)、若将上面第（3）问中“实行每日计件工资制”改为“实行每周计件工资制”，其他条件不变，在此方式下小明妈妈这一周的工资与按日计件的工资哪一个更多？请说明理由．

查看试题解析
25. 素材1：每年秋天是灵昆柿子饼盛产期．小黄同学打算从灵昆寄5袋柿子饼到杭州，以每袋3千克为标准，超过的千克数记为正数，不足的千克数记为负数，记录如下表所示：
柿子饼袋
①
②
③
④
⑤
与标准重量的差值（单位：千克）
0.1
-0.3
0
-0.1
0.2
素材2：小黄同学选择了某快递，收费标准如下：3千克以内15元（含3千克），超过1千克的部分为2元/每千克（不足1千克按1千克计）．现该快递公司提供多种寄件方式：
纸箱类型
中型纸箱
大型纸箱
可容纳袋数（袋/个）
2
4
重量（千克/个）
0.4
0.7
价格（元/个）
3
5
方案一：小黄购买了中型纸箱将重量最低的②、④柿子饼袋打包在一起，其余每小袋各自寄出．
方案二：____．

(1)、【任务1】求这5袋柿子饼的总重量．

(2)、【任务2】求方案一所需要的费用．

(3)、【任务3】请你设计方案二，使它的费用低于方案一，并计算你的方案费用．

查看试题解析

价目表
每月用水量	单价
不超出 $6 m^{3}$ 的部分	3元/ $m^{3}$
超出 $6 m^{3}$ 但不超出 $10 m^{3}$ 的部分	5元/ $m^{3}$
超出 $10 m^{3}$ 的部分	9元/ $m^{3}$
注：水费按月结算．

星期	一	二	三	四	五	六	日
增减产值	＋10	－12	－4	＋8	－1	＋6	0

柿子饼袋	①	②	③	④	⑤
与标准重量的差值（单位：千克）	0.1	-0.3	0	-0.1	0.2

纸箱类型	中型纸箱	大型纸箱
可容纳袋数（袋/个）	2	4
重量（千克/个）	0.4	0.7
价格（元/个）	3	5

【培优卷】湘教版（2024）七年级上册1.7 有理数的混合运算 同步练习

一、选择题

二、填空题

三、计算题

四、解答题

【培优卷】湘教版（2024）七年级上册1.7 有理数的混合运算同步练习