浙教版数学八上第2章章末重难点专训 勾股定理的广泛应用
试卷更新日期：2024-08-28 类型：复习试卷
一、选择题
-
1. 如图，A，C之间隔有一湖，在与方向成角的方向上的点B处测得 ， ， 则AC的长为（ ）
A、 B、 C、 D、2. 如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是 3、4、1、3， 则最大的正方形 E的面积是( )
A、11 B、47 C、26 D、353. 在《算法统宗》中有一道“荡秋千”的问题：“平地秋千未起，踏板一尺离地送行二步与人齐，五尺人高曾记．仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索长有几．”此问题可理解为：如图，有一架秋千，当它静止时，踏板离地距离长度为1尺．将它往前水平推送10尺时，即＝10尺，则此时秋千的踏板离地距离就和身高5尺的人一样高．若运动过程中秋千的绳索始终拉得很直，则绳索长为（ ）
A、13.5尺 B、14尺 C、14.5尺 D、15尺4. 如图，小明欲控制遥控轮船匀速垂直横渡一条河，但由于水流的影响，实际上岸地点C与欲到达地点B相距10米，结果轮船在水中实际航行的路程比河的宽度多2米，则河的宽度是（ ）
A、8米 B、12米 C、16米 D、24米5. 如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆8 m处，发现此时绳子末端距离地面2 m，则旗杆的高度(滑轮上方的部分忽略不计)为（ ）
A、12 m B、13 m C、16 m D、17 m6. 如图，在中， ， 以的各边为边在外作三个正方形，、、分别表示这三个正方形的面积，若 ， ， 则的值是（ ）
A、5 B、8 C、10 D、167. 如图，在高为 ，坡面长为 的楼梯表面铺地毯，地毯的长度至少需要（ ）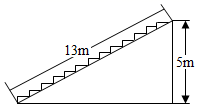
A、 B、 C、 D、8. 某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动．如图，当张角为时，顶部边缘处距离桌面的高度为 ， 此时底部边缘处与处间的距离为 ， 小组成员调整张角的大小继续探究，最后发现当张角为时（是的对应点），顶部边缘处到桌面的距离为 ， 则底部边缘处与之间的距离为（ ）
A、 B、 C、 D、二、填空题
-
9. 勾股定理是人类数学文化的一颗璀璨明珠，是用代数思想解决几何问题最重要的工具，也是数形结合的纽带之一．如图，当秋千静止时，踏板离地的垂直高度 ， 将它往前推至处时（即水平距离），踏板离地的垂直高度 ， 它的绳索始终拉直，则绳索的长是 ．
10. 我国古代数学名著（孙子算经）有估算方法：“方五，邪（通“斜”）七。见方求邪，七之，五而一。”译文为：如果正方形的边长为五，则它的对角线长为七．已知正方形的边长，求对角线长，则先将边长乘以七再除以五．若正方形的边长为1，由勾股定理得对角线长为 ，依据《孙子算经》的方法，则它的对角线的长是 ．11. 刷牙是我们每天都要做的事，坚持早、晚刷牙有利于健康.如图，是一把长为15cm的牙刷置于底面直径为6cm，高为8cm的圆柱形水杯中，牙刷露在杯子外面的长度为cm，则的取值范围是cm.
12. 如图，所有的四边形是正方形，所有的三角形都是直角三角形，其中最大的正方形面积为9cm2 ，则图中所有的正方形的面积之和为 cm2 ．
13. 在我国古代数学著作《九章算术》“勾股”章有一题：“今有开门去间（kǔn）一尺，不合二寸，向门广几何.”大意是说：如图，推开两扇门（和），门边缘、两点到门槛的距离为1尺（1尺=10寸），两扇门间的缝隙为2寸， ， 那么门的宽度即的长为寸.
三、解答题
-
14. 为推进乡村振兴，把家乡建设成为生态宜居、交通便利的美丽家园，某地大力修建崭新的公路.如图，现从A地分别向C、D、B三地修了三条笔直的公路AC，AD和AB，C地、D地、B地在同一笔直公路上，公路AC和公路CB互相垂直，又从D地修了一条笔直的公路DH与公路AB在H处连接，且公路DH和公路AB互相垂直，已知AC=9千米，AB=15千米，BD=5千米.
(1)、求公路CD、AD的长度；(2)、若修公路DH每千米的费用是2万元，请求出修建公路DH的费用．15. 在一条东西走向河的一侧有一村庄C ， 河边原有两个取水点A ， B ， 其中 ， 由于某种原因，由C到A的路现在已经不通，某村为方便村民取水，决定在河边新建一个取水点H（A、H、B在一条直线上），并新修一条路CH ， 测得千米，千米，千米．
(1)、问CH是否为从村庄C到河边的最近路﹖请通过计算加以说明；(2)、求原来的路线AC的长．16. 某军舰以每小时20海里的速度由西向东航行，一艘电子侦察船以每小时30海里的速度由南向北航行，它能侦察出周围50海里（包括50海里）范围内的目标．如图，当该军舰行至处时，电子侦察船正位于处正南方向的处，且海里．如果军舰和侦察船仍按原速度沿原方向继续航行，那么航行途中侦察船能否侦察到这艘军舰？如果能，最早何时能侦察到？如果不能，请说明理由．
17. 勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理． 在我国古书《周髀算经》中就有“若勾三，股四， 则弦五”的记载， 我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图” （如图 ①， 后人称之为 “赵爽弦图”， 流传至今．
(1)、 ①请叙述勾股定理．②勾股定理的证明， 人们已经找到了 400 多种方法， 请从以下三种常见的证明方法中任选一种来证明该定理 （图 ①②③均满足证明勾股定理所需的条件）．
(2)、 ①如图④⑤⑥， 以直角三角形的三边为边或直径， 分别向外部作正方形、半圆、等边三角形，这三个图形中面积关系满足 的有 ▲ 个．②如图⑦， 分别以直角三角形三边为直径作半圆， 设图中两个月牙形图案（图中阴影部分） 的面积分别为 ， ， 直角三角形的面积为 ， 请判断 的数量关系并证明．
四、综合题
-
18. 在一款名为超级玛丽的游戏中，玛丽到达一个高为10米的高台A，利用旗杆顶部的绳索，划过90°到达与高台A水平距离为17米，高为3米的矮台B，
(1)、求高台A比矮台B高多少米？
(2)、求旗杆的高度OM；
(3)、玛丽在荡绳索过程中离地面的最低点的高度MN．
19. 台风是一种自然灾害，它以台风中心为圆心在周围上百千米的范围内形成极端气候，有极强的破坏力，如图，有一台风中心沿东西方向 由 行驶向 ，已知点 为一海港，且点 与直线 上的两点 ， 的距离分别为 ， ，又 ，以台风中心为圆心周围 以内为受影响区域．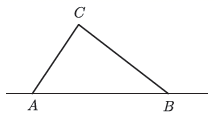
(1)、求 的度数．(2)、海港 受台风影响吗？为什么？(3)、若台风的速度为20千米/小时，当台风运动到点 处时，海港 刚好受到影响，当台风运动到点 时，海港 刚好不受影响，即 ，则台风影响该海港持续的时间有多长？